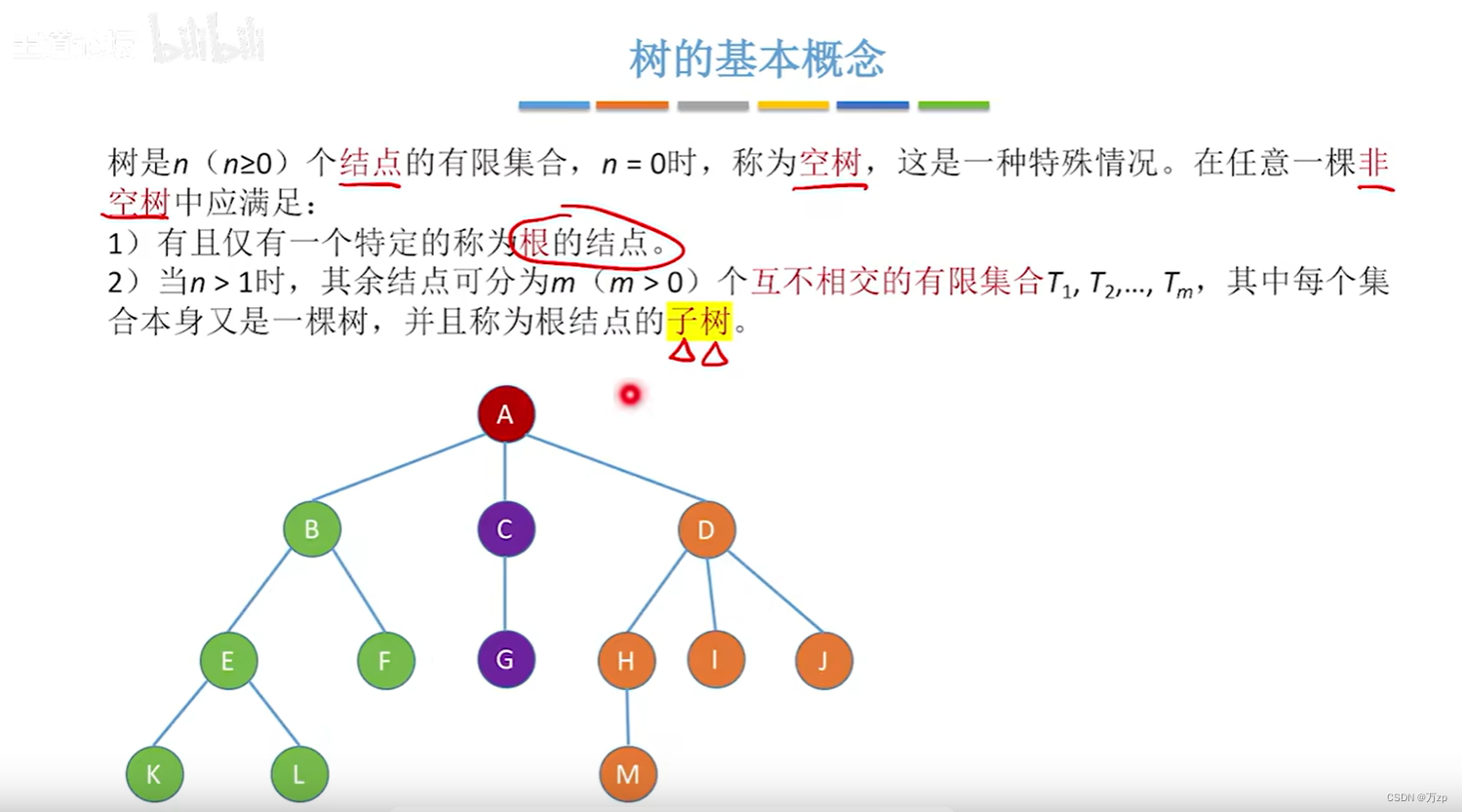
01.树

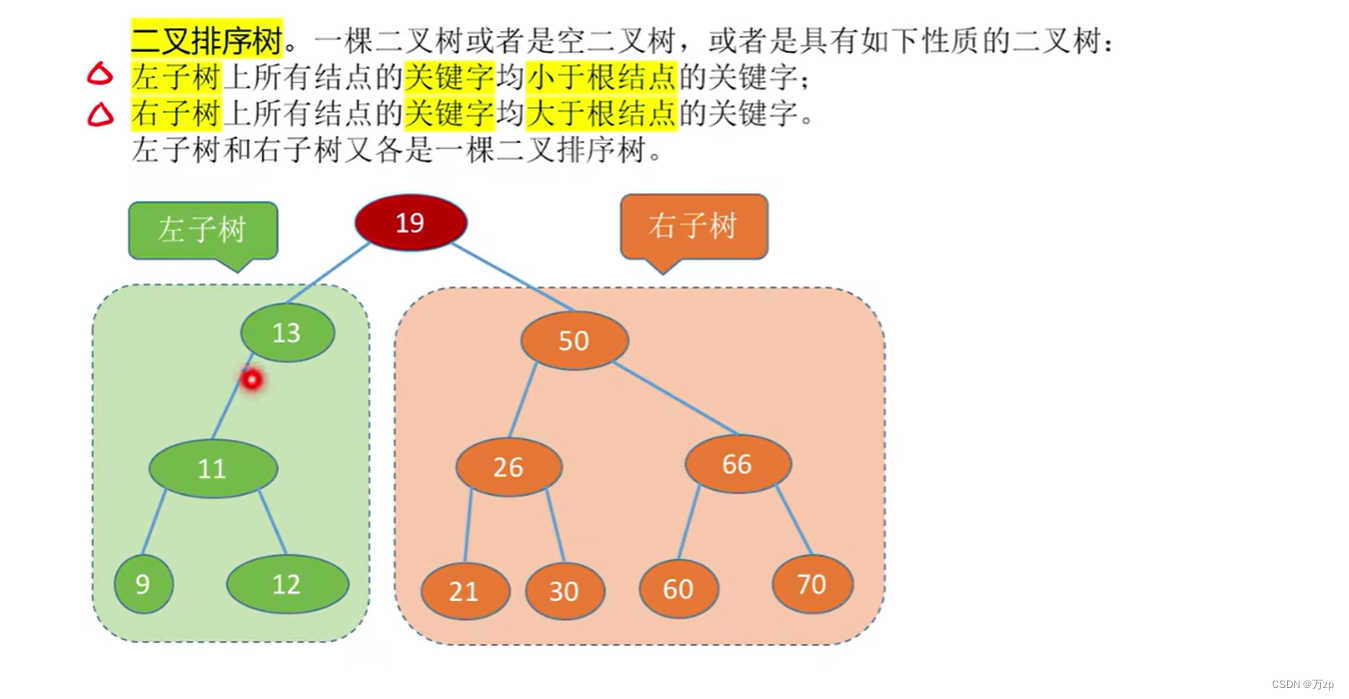
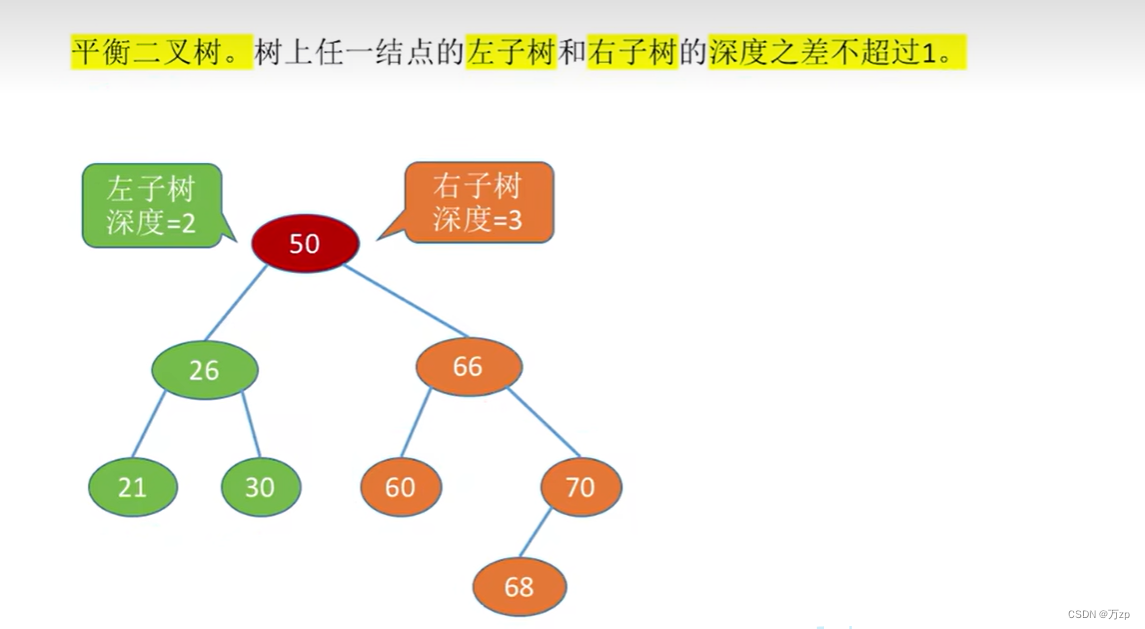
02.二叉树和二叉平衡树
03.平衡二叉树的恢复

将导致不平衡的结点称作被破坏者,破坏了结点的平衡的结点成为破坏者,经过调整可以让该树平衡的结点称为调整结点。
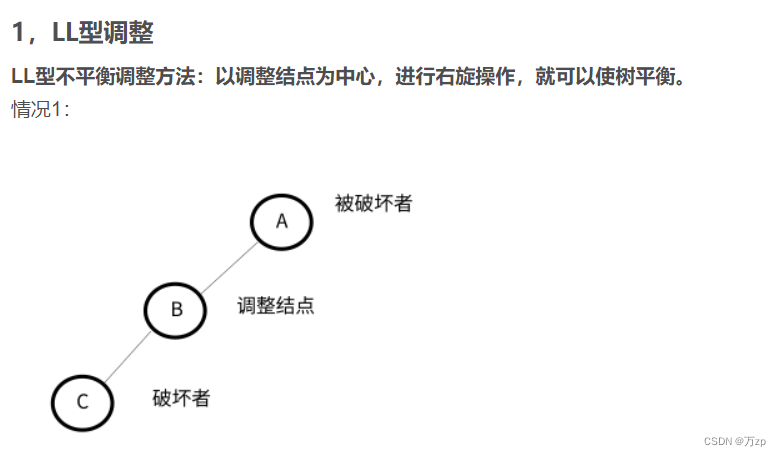
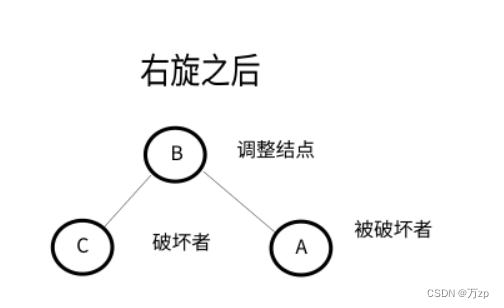
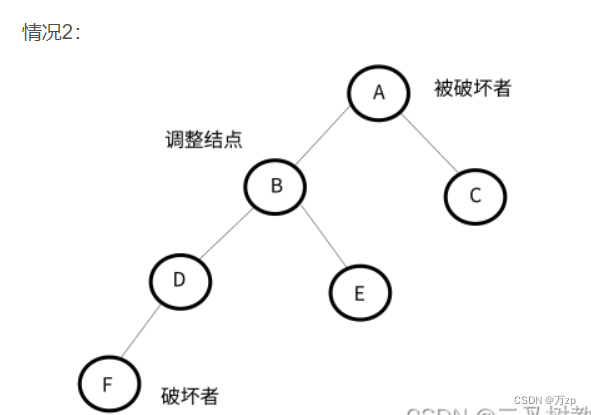
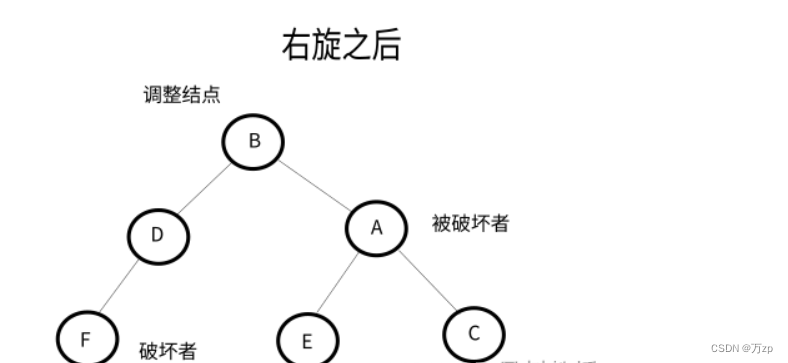
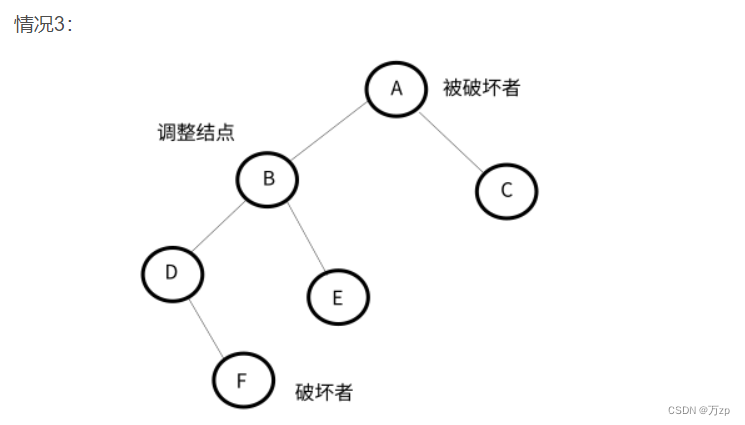
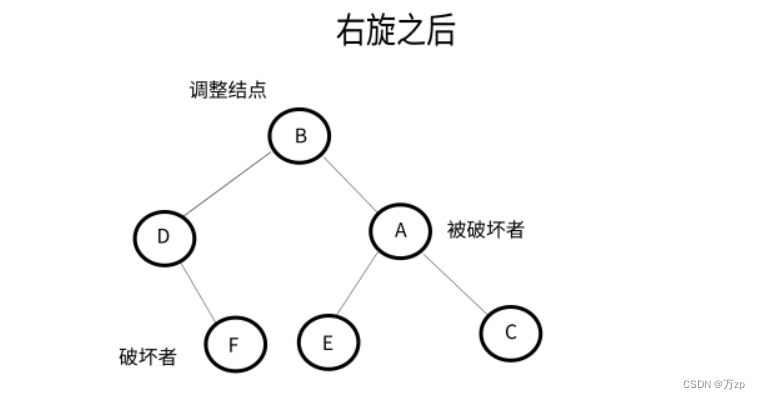
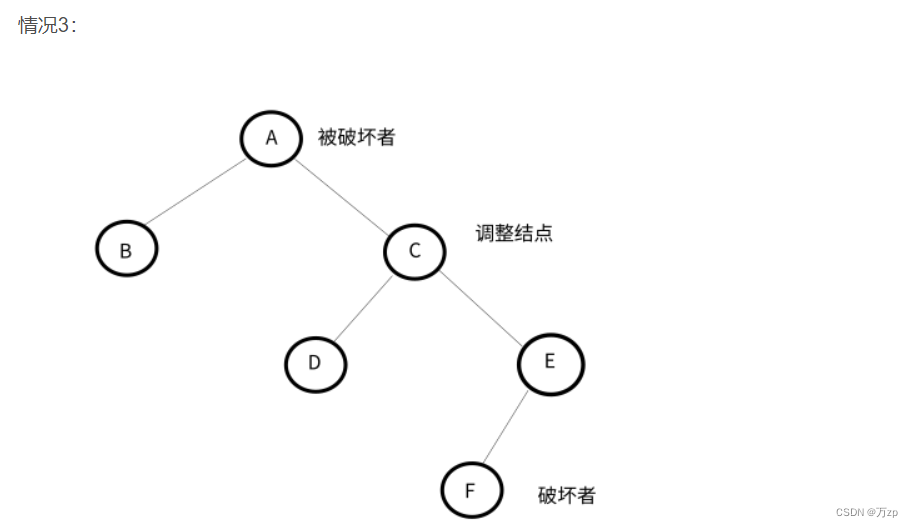
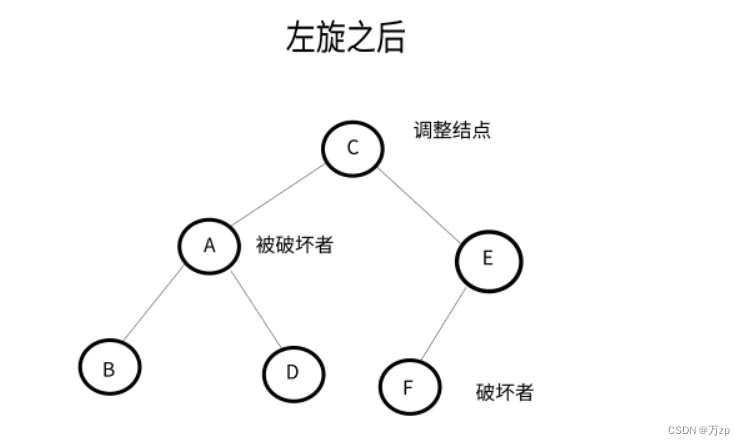

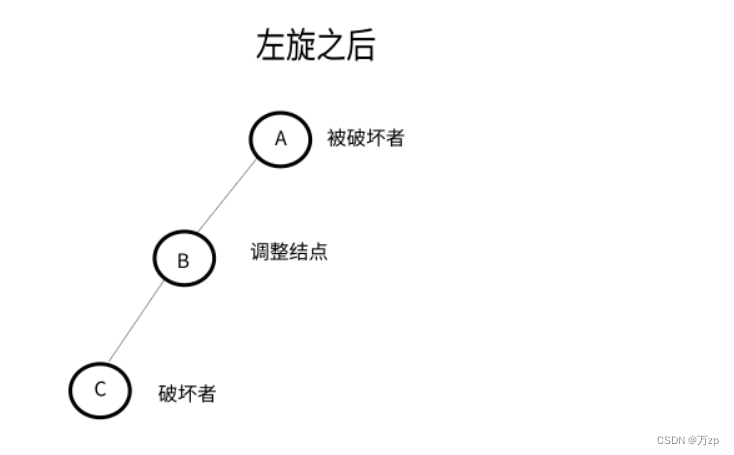

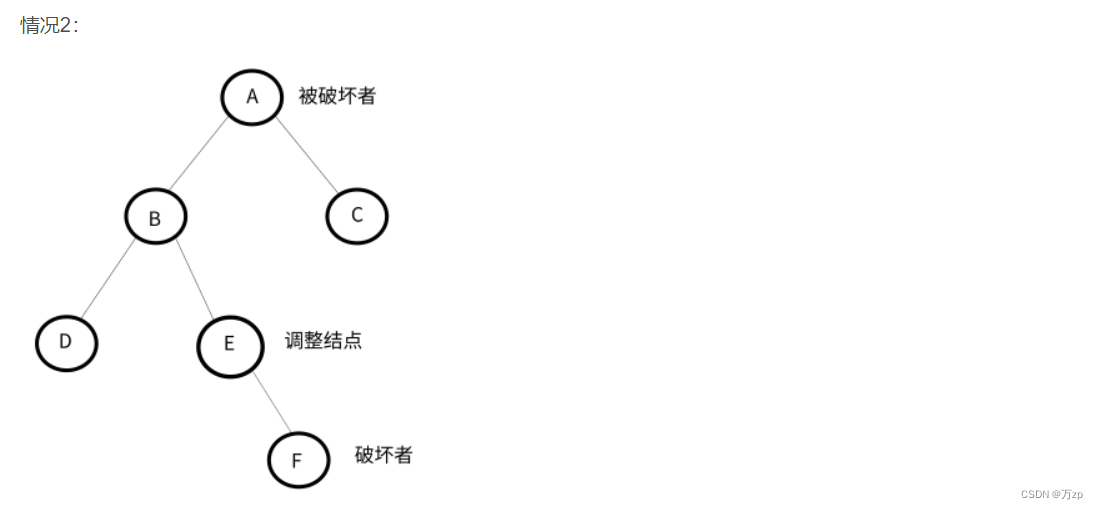


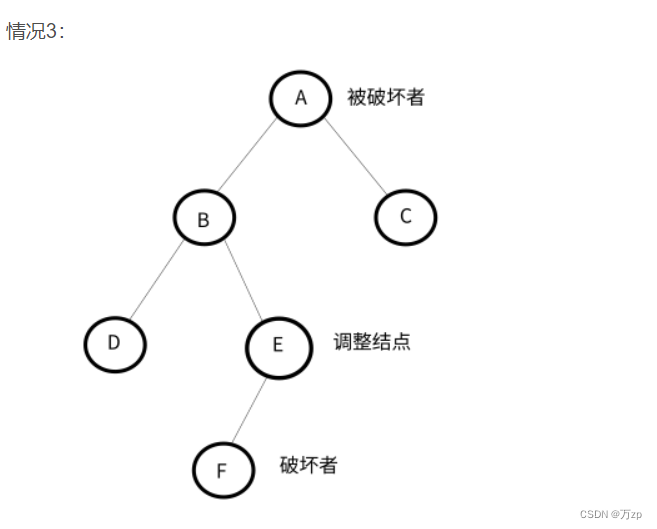


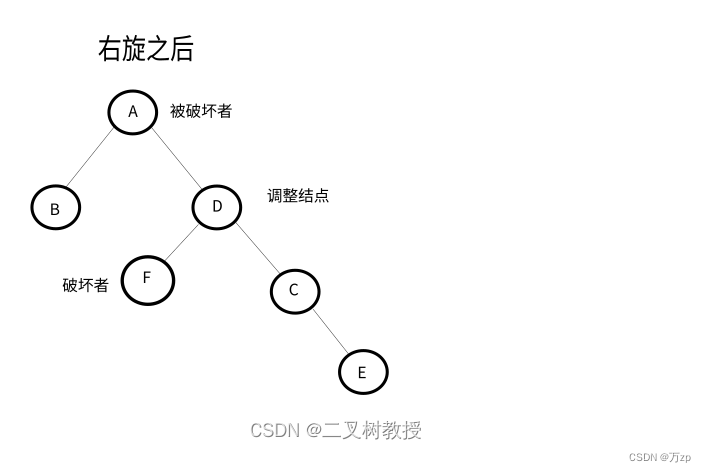
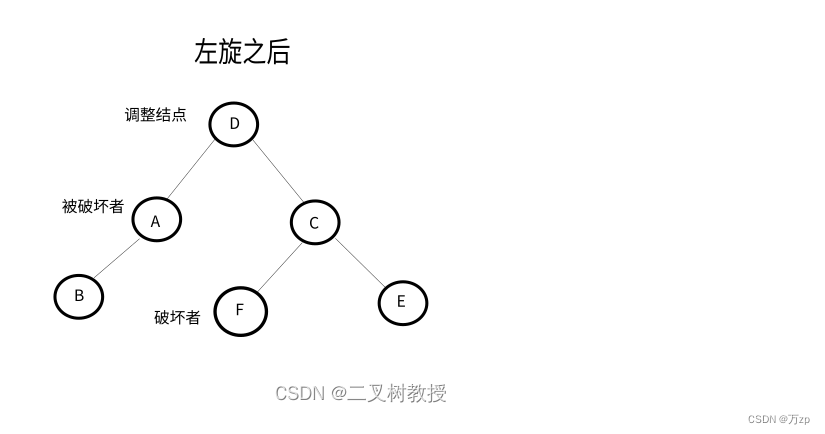
LL型:
以被破坏者的左孩子结点作为调整结点,对其进行右旋。如果调整结点有右子树,将其右子树作为被破坏者的左子树。
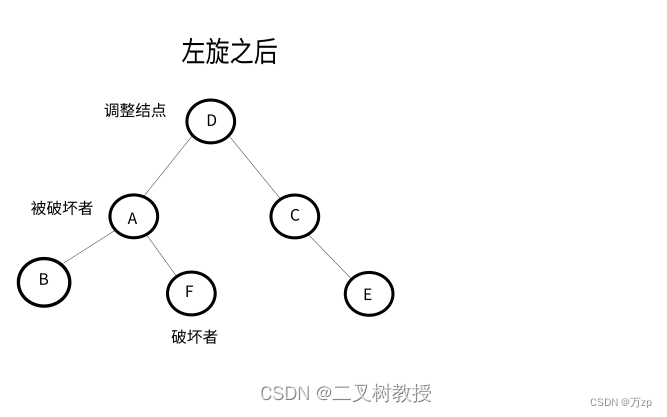
LR型:
以被破坏者的左孩子的右孩子结点为调整结点。
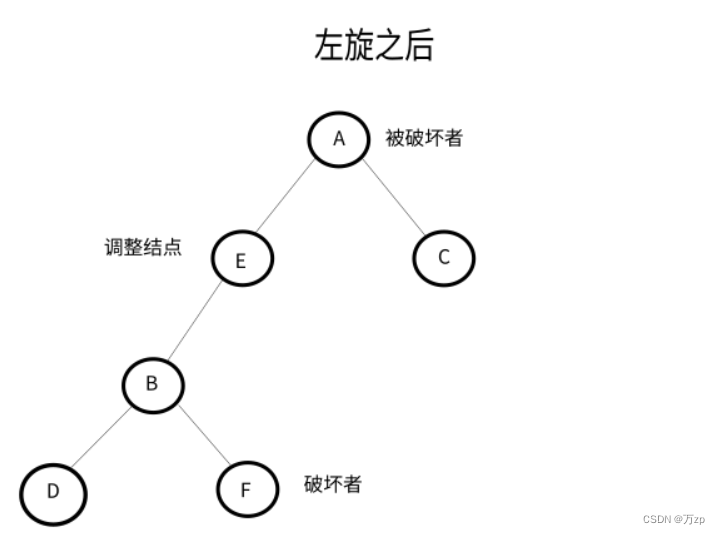
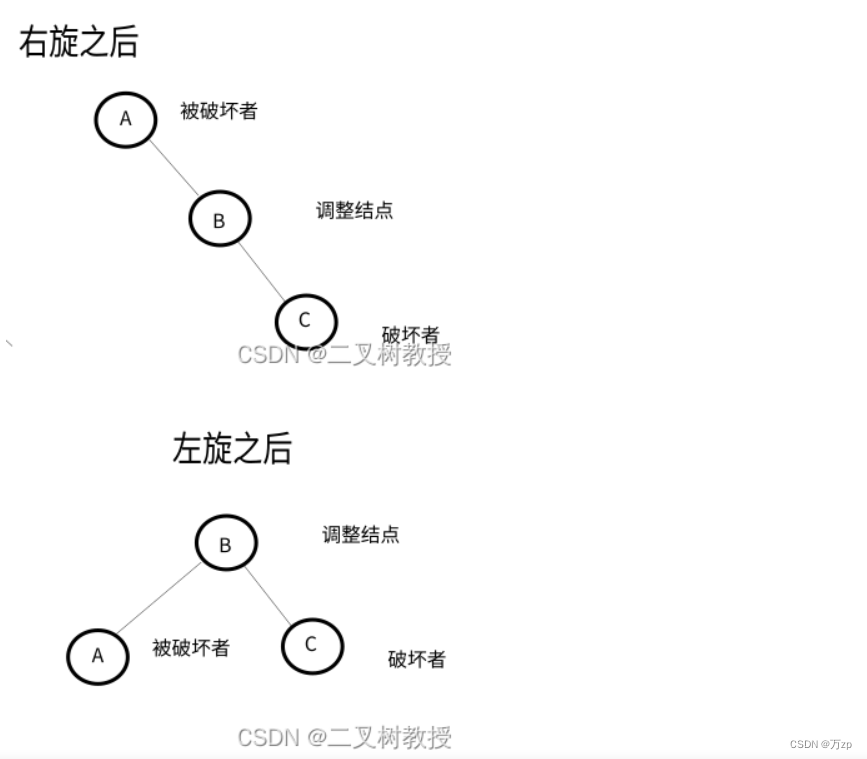
如果破坏者为调整结点的左孩子,以调整结点进行左旋,将破坏者作为调整结点的父节点的右子树,后进行右旋,破坏者位置保持不变。
如果破坏者为调整结点的右孩子,以调整结点进行左旋,破坏者位置保持不变。后进行右旋,将破坏者作为被破坏者的左子树。
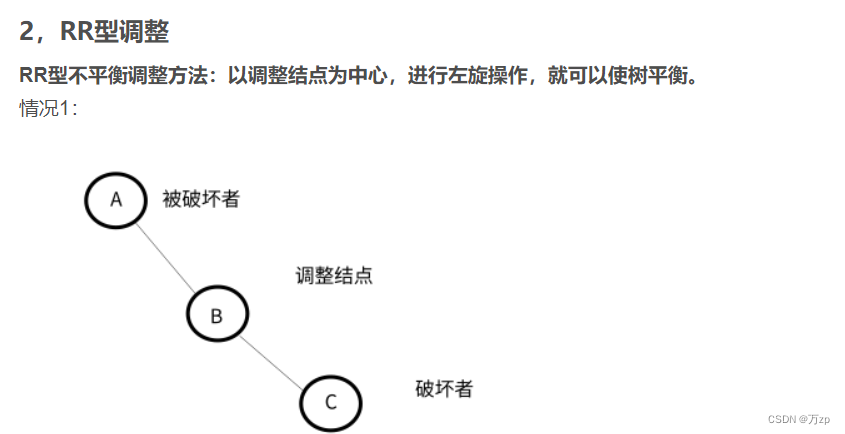
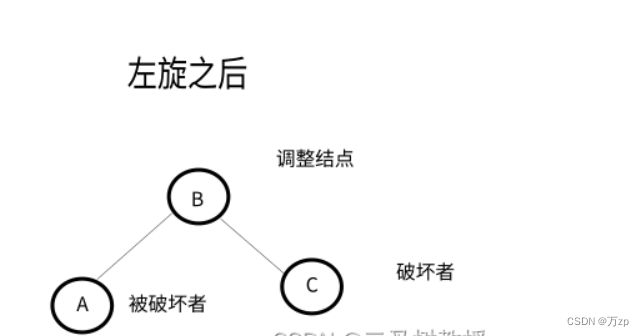
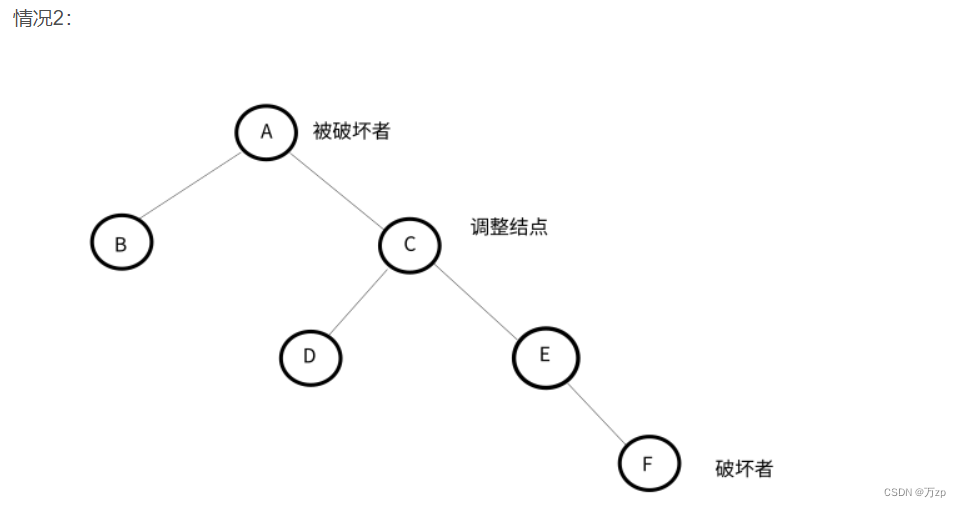
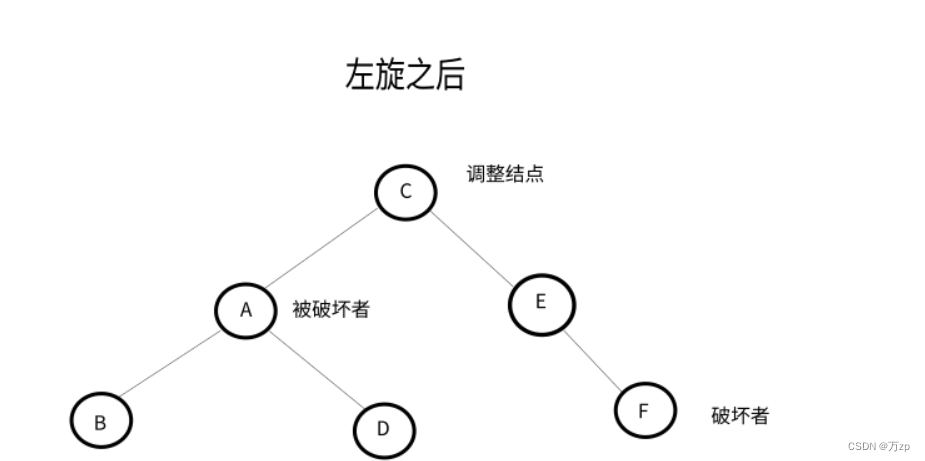
RR型:
以被破坏者的右孩子结点为调整结点,对其进行左旋。如果调整结点有左子树,将其右子树作为被破坏者的右子树。
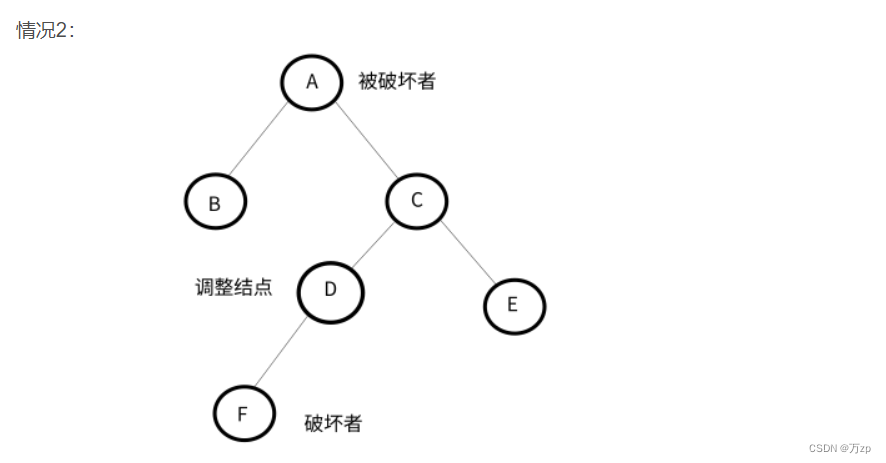
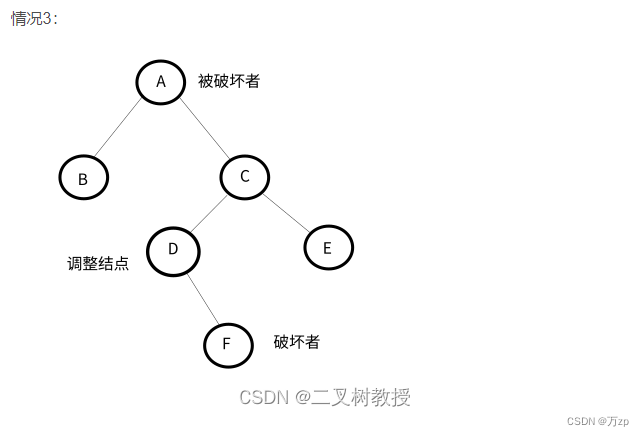
RL型:
以被破坏者的右孩子的左孩子结点为调整结点。
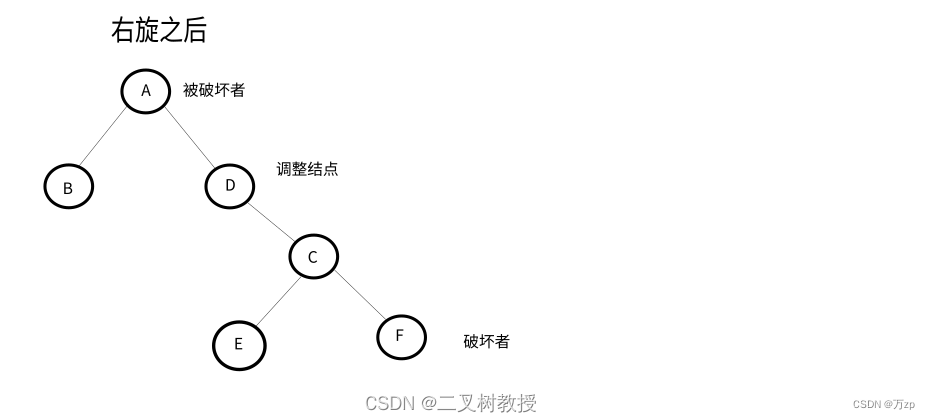
如果破坏者为调整结点的左孩子,以调整结点进行右旋,破坏者位置保持不变,后进行左旋,将破坏者作为被破坏者的右子树。
如果破坏者为调整结点的右孩子,以调整结点进行右旋,将破坏者作为调整结点的父节点的左子树。后进行左旋,破坏者位置保持不变。
红黑树:
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。
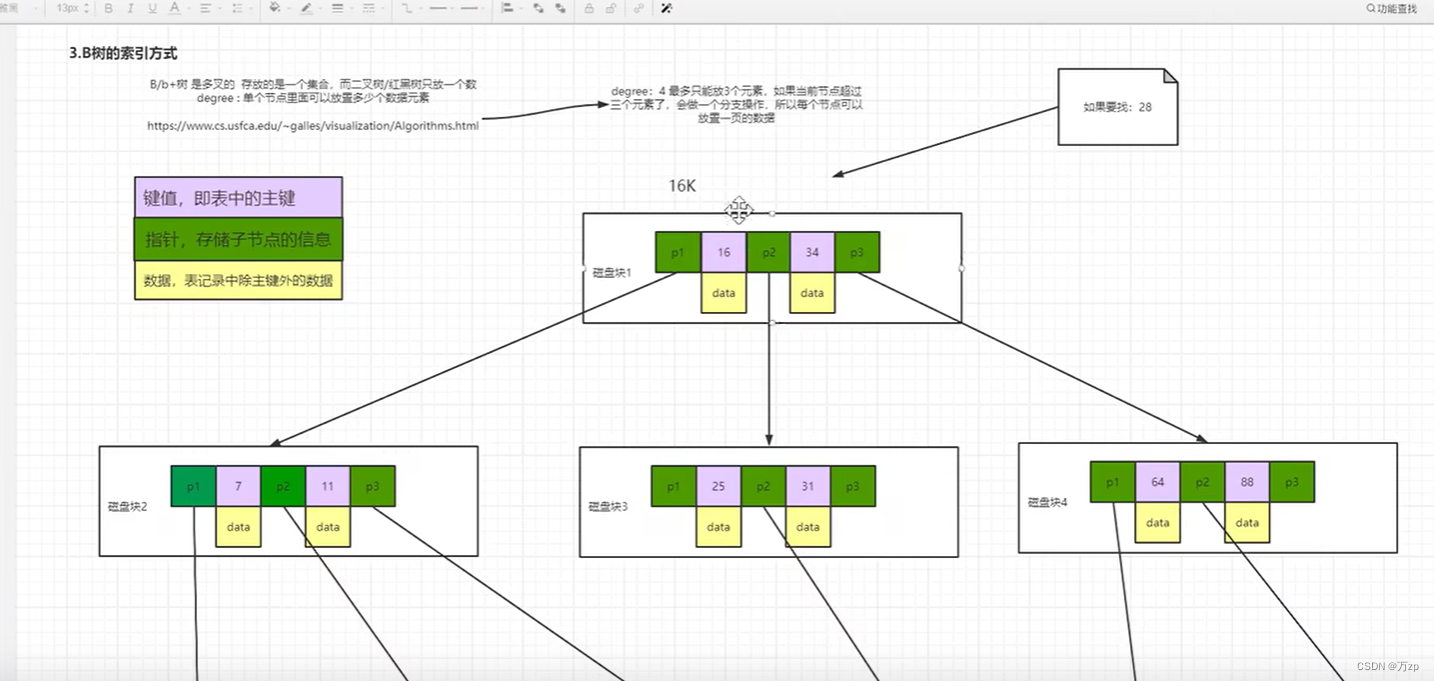
B树:(m阶查找树)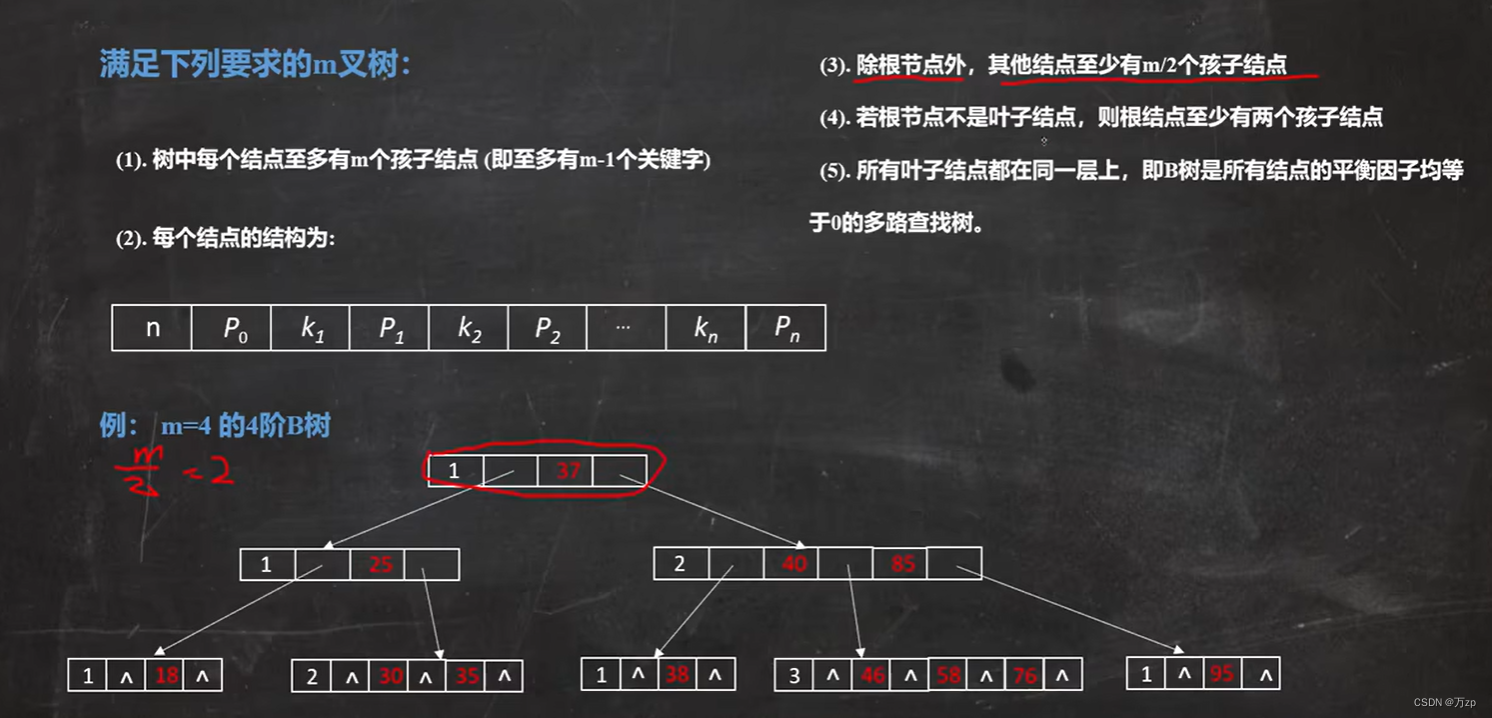
节点结构中的
n记录关键字的个数
k是关键字
p是指针
一颗m阶的B树满足如下条件:
- 每个节点最多只有m个子节点(节点内至多m-1关键字)。
- 除根节点外,每个非叶子节点具有至少有 m/2(向下取整)个子节点。
- 非叶子节点的根节点至少有两个子节点。
- 有k颗子树(k个孩子节点)的非叶节点有k-1个键,键按照递增顺序排列。 叶节点都在同一层中。
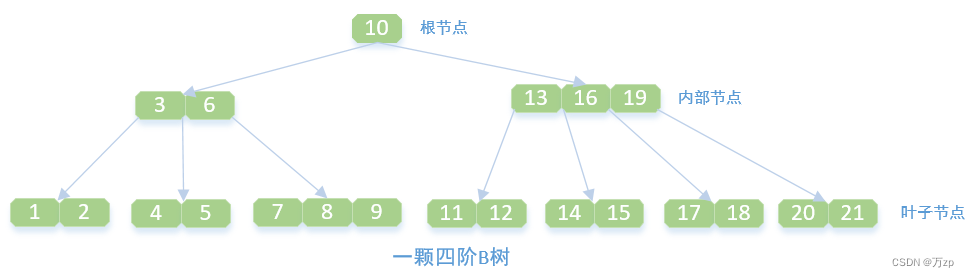
(1)什么是B树的阶 ?
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为4,则为4阶,如图,所有节点中,节点[13,16,19]拥有的子节点数目最多,四个子节点(灰色节点),所以可以定义上面的图片为4阶B树。
(2)什么是根节点 ?
节点【10】即为根节点,特征:根节点拥有的子节点数量的上限和内部节点相同,如果根节点不是树中唯一节点的话,至少有俩个子节点(不然就变成单支了)。在m阶B树中(根节点非树中唯一节点),那么有关系式2<= M <=m,M为子节点数量;包含的元素数量 1<= K <=m-1,K为元素数量。
(3)什么是内部节点 ?
节点【13,16,19】、节点【3,6】都为内部节点,特征:内部节点是除叶子节点和根节点之外的所有节点,拥有父节点和子节点。假定m阶B树的内部节点的子节点数量为M,则一定要符合(m/2)<= M <=m关系式,包含元素数量M-1;包含的元素数量 (m/2)-1<= K <=m-1,K为元素数量。m/2向上取整。
(4)什么是叶子节点?
节点【1,2】、节点【11,12】等最后一层都为叶子节点,叶子节点对元素的数量有相同的限制,但是没有子节点,也没有指向子节点的指针。特征:在m阶B树中叶子节点的元素符合(m/2)-1<= K <=m-1。