题目
有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,…,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。
在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i][j] 由 [0,1,…,N-1]
中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。最初,除 0 号房间外的其余所有房间都被锁住。
你可以自由地在房间之间来回走动。
如果能进入每个房间返回 true,否则返回 false。
示例 1:
输入: [[1],[2],[3],[]] 输出: true 解释: 我们从 0 号房间开始,拿到钥匙 1。 之后我们去 1 号房间,拿到钥匙
2。 然后我们去 2 号房间,拿到钥匙 3。 最后我们去了 3 号房间。 由于我们能够进入每个房间,我们返回 true。 示例 2:输入:[[1,3],[3,0,1],[2],[0]] 输出:false 解释:我们不能进入 2 号房间
思路
DFS和BFS的区别
DFS(深度优先搜索): dfs是朝一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就是回溯的过程)
BFS(广度优先搜索):bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是发散,四面八方的搜索过程。
总结:
- 广搜(bfs)是一圈一圈的搜索过程,广搜队列
- 深搜(dfs)是一条路跑到黑然后再回溯,深度递归
DFS实现代码:
因为dfs朝着一个方向搜索,并且需要回溯,所以使用递归来实现最方便的
一般情况,深搜需要二维数组数组结构保存所有路径(结果集),需要一维数组保存单一路径(单条结果)
dfs代码框架和回溯代码框架几乎差不多,如下:
void dfs(参数){
if(终止条件){
存放结果;
return;
}
for(选择:本节点所连接的其他节点){
处理节点;
dfs(图,选择的节点);//递归
(回溯,撤销处理结果);//根据题意,是否需要还原节点,即回溯
}
}
BFS实现代码:
广搜适合解决两个点之间的最短路径问题。
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路(正是因为BFS一圈一圈的遍历方式,所以一旦遇到终止点,那么一定是一条最短路径),即只要BFS搜到终点一定是一条最短路径。
当然,也有一些问题是广搜和深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
注意:BFS实现的容器并非只能用队列实现,bfs只是仅仅需要一个容器,能保存要遍历过的元素就可以,用队列,还是用栈,甚至用数组,都是可以的。
- 用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针;因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
- 用栈的话,可能就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈又顺时针遍历;因为栈是先进后出,加入元素和弹出元素的顺序改变了。但是广搜不需要注意转圈搜索的顺序吗
所以用队列,还是用栈都是可以的,只是大家都习惯用队列(FIFO先进先出)了,只不过要清楚,BFS并不是非要用队列,用栈也可以
bfs代码框架:
void bfs(){
初始化队列Q;
Q = {起始节点s};
标记s已访问;
while(que非空){
取Q队首元素u;
u出队;
if(u == 目标状态){
...
}
所有与u相邻且未被访问的点进入队列;
标记u为已访问;
}
}
最后回到本题,本题给出的其实是一个有向图,对于题中的示例[[1],[2],[3],[]] [[1,3],[3,0,1],[2],[0]],画成对应的图为:

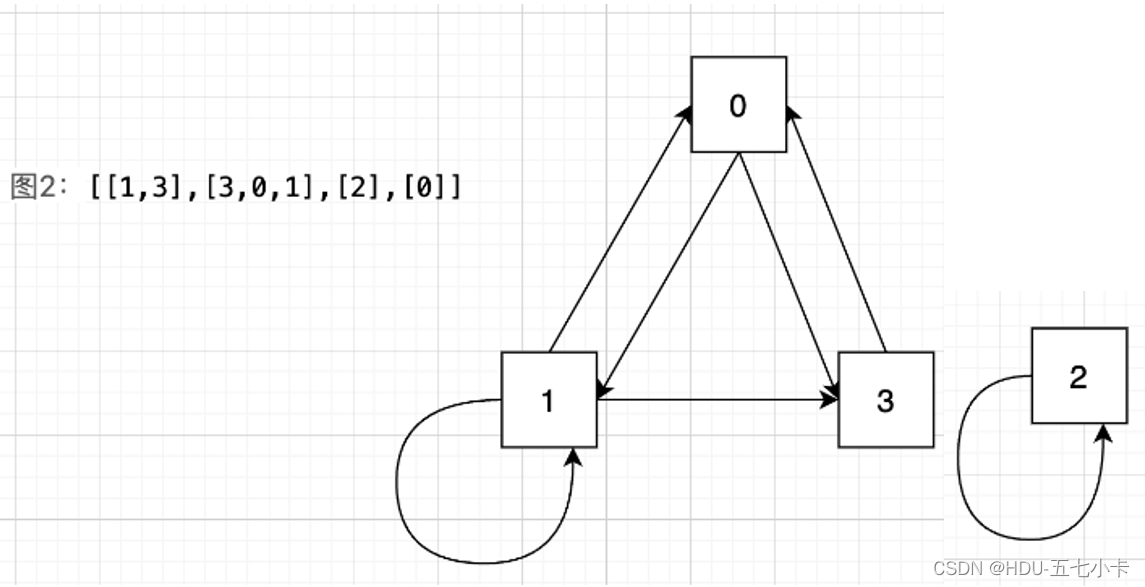
当 x 号房间中有 y 号房间的钥匙时,就可以从 x 号房间去往 y 号房间。如果将这 n 个房间看成有向图中的 n 个节点,那么上述关系就可以看作是图中的 x 号点到 y号点的一条有向边。这样一来,问题就变成了给定一张有向图,询问从 0 号节点出发是否能够到达所有的节点
所以本题是一个有向图搜索全路径的问题, 只能用深搜(DFS)或者广搜(BFS)来搜。
方法一:DFS
使用深度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 vis 标记当前节点是否访问过,以防止重复访问
java代码如下:
class Solution {
//一定要定义成全局变量,否则只能一个函数调用
int num;//记录能够到达的房间数
boolean[] vis;//判断是否去过该房间
public boolean canVisitAllRooms(List<List<Integer>> rooms){
int n = rooms.size();
num = 0;
vis = new boolean[n];
dfs(rooms,0);
return n == num;
}
public void dfs(List<List<Integer>> rooms, int x){
vis[x] = true;
num++;
for(int u : rooms.get(x)){//这里get(x)取出的是一个列表,表示的是当前房间的钥匙,即可以去往哪些房间
if(!vis[u]){//如果u未被访问过,即没去过这个房间
dfs(rooms,u);
}
}
}
}
方法二:BFS
使用广度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 vis 标记当前节点是否访问过,以防止重复访问
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms){
int n = rooms.size();
int num = 0;//记录可以到达的节点个数
boolean[] vis = new boolean[n];
Queue<Integer> que = new LinkedList<Integer>();
que.offer(0);
vis[0] = true;
while(!que.isEmpty()){
int x = que.poll();
num++;
for(int u : rooms.get(x)){//这里get(x)取出的是一个列表,表示的是当前房间的钥匙,即可以去往哪些房间
if(!vis[u]){//如果u未被访问过,即没去过这个房间
que.offer(u);
vis[u] = true;
}
}
}
return num == n;
}
}
- 时间复杂度:O(n+m),其中 n 是房间的数量,m 是所有房间中的钥匙数量的总数
- 空间复杂度:O(n),其中 n 是房间的数量,主要为队列的开销