假设法做线段树

news2024/11/19 9:31:02

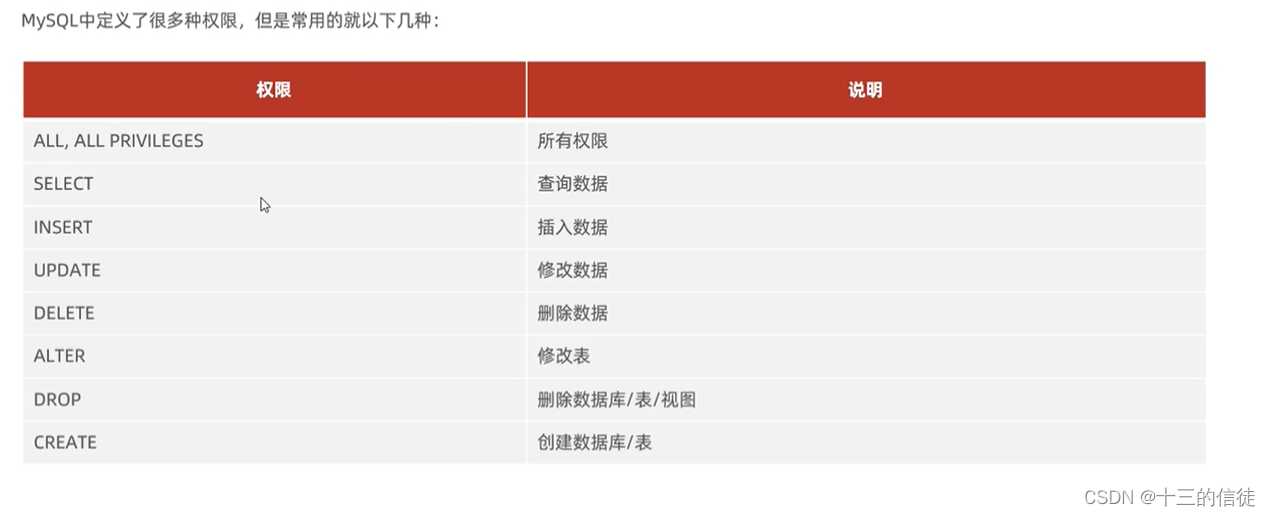
合并lazy-tag：指的是把一些能合并的合并了，如果有多种 lazy-tag 的话，每一层最多只存在一个tag。

下面，这是一道区间乘与区间加的混合。

P3373 【模板】线段树 2 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P3373

ps：（sum、add、len、mul，分别表示当前区间的区间和、加标记、长度，乘标记）

总的说来，我们可以把这道题分为两种情况：

1、先加后乘： sum = (sum+add*len ) * mul

2、先乘后加： sum = sum*mul +add*len

然后尝试一下能不能合并为一种情况。

对于1，我们只要把它展开： sum = sum*mul + add*mul * len

我们发现，这两种形式是相同的。

我们就可以考虑将他们写在同一个pushdown里面。

这样向下传递完了之后，mul和add标记都被清除

所以我们的pushdown可以这样写：

void pushdown1(int pos) {

	ll mid = (L + R) >> 1;
	Lv = ((Lv * Mul) + Add * (mid - L + 1)) % mod;
	Rv = ((Rv * Mul) + Add * (R -mid)) % mod;


	LMul = (LMul * Mul) % mod;
	RMul = (RMul * Mul) % mod;


	LAdd = (LAdd*Mul  + Add) % mod;
	RAdd = (RAdd*Mul  + Add) % mod;


	Add = 0;
	Mul = 1;

}

这时候，又有疑问了，因为我们只有在先加后乘的情况下，左右儿子的加法标记才能更新为：LAdd*Mul + Add 的形式啊。

为什么先乘后加和先加后乘共用一个 pushdown？

先乘后加中下传的add为什么要乘mul？

正是因为它们形式是一样的，共用了一个pushdown后可以同时清除两个标记，然后诡异的使得每个pos中只有一个标记！

这个很抽象，请往下看。

在这道题中：

要么没有标记，要么只有加标记，要么只有乘标记。

如果是先乘后加，那么其实乘标记的值是1.

所以不会影响正确的值。

那我是怎么得出这个结论的呢?

// 乘法操作
void mul(int pos, int ql, int qr, int val) {

	pushdown1(pos);
	if (ql <= L and qr >= R) {
		Mul = (Mul * val) % mod;
		V = (V * val) % mod;
		return;
	}


	ll mid = (L + R) >> 1;
	if (ql <= mid)mul(lson, ql, qr, val);
	if (qr > mid)mul(rson, ql, qr, val);


	pushup(pos);
	return;
}


//加法操作
void add(int pos, int ql, int qr, int val) {
	pushdown1(pos);
	if (ql <= L and qr >= R) {

		V = (V + (R - L + 1) * val) % mod;
		Add = (Add + val) % mod;

		return;
	}

	ll mid = (L + R) >> 1;
	if (ql <= mid)add(lson, ql, qr, val);
	if (qr > mid)add(rson, ql, qr, val);


	pushup(pos);
	return;
}

注意看我写的乘法和加法操作。

pushdown放在了if判断的前面。

可以证明当我们还没进入if 的时候，我们就已经执行了pushdown。

然后进入if之后，此时pos的所有标记已经被初始化了。

而，进入if后，每次执行乘法或加法的时候，只会更新乘法标记或加法标记。

所以，理论上是每一个pos最多只有一种标记的。

所以这道题就能解释的清楚了。

然后我们捋一下思路：

知道这道题中，每个pos只存在一种lazy-tag。

然后将这题分成两种情况：

先加后乘，先乘后加。

发现先加后乘可以整理为先乘后加的形式。