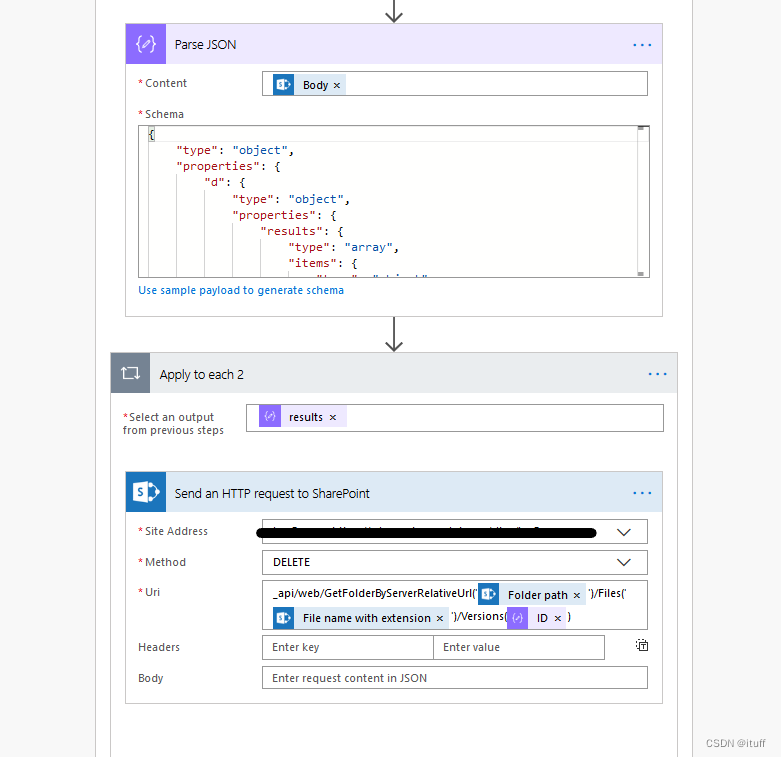
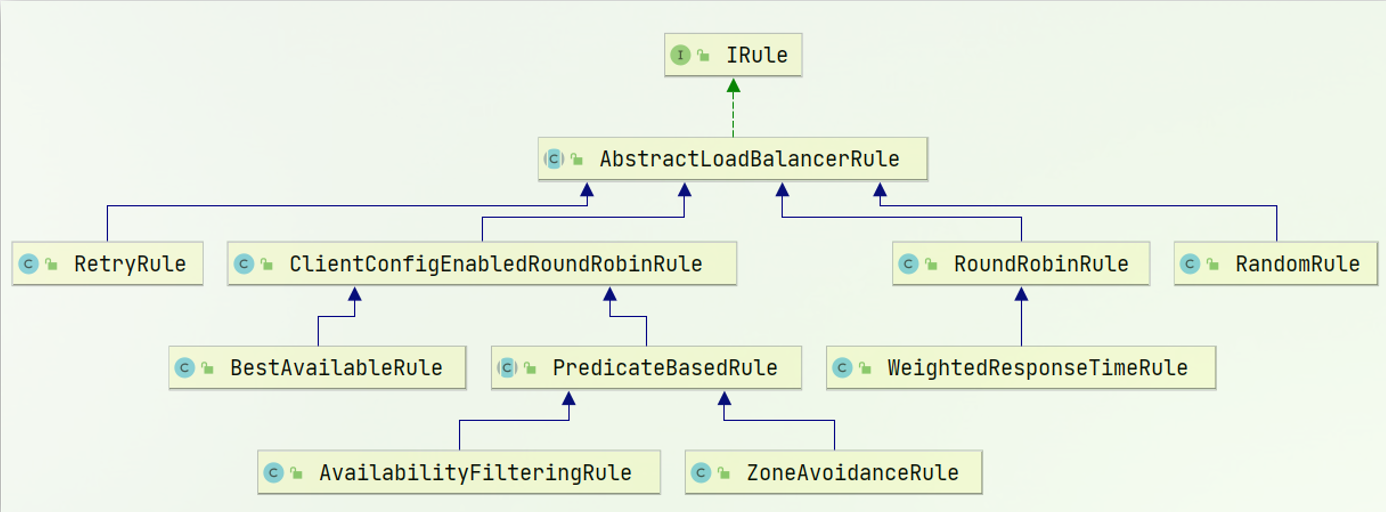
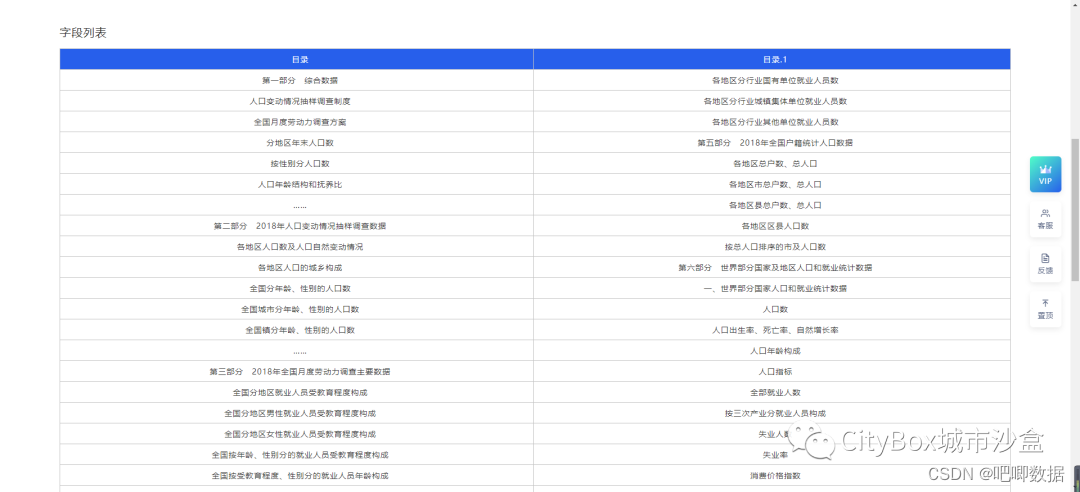
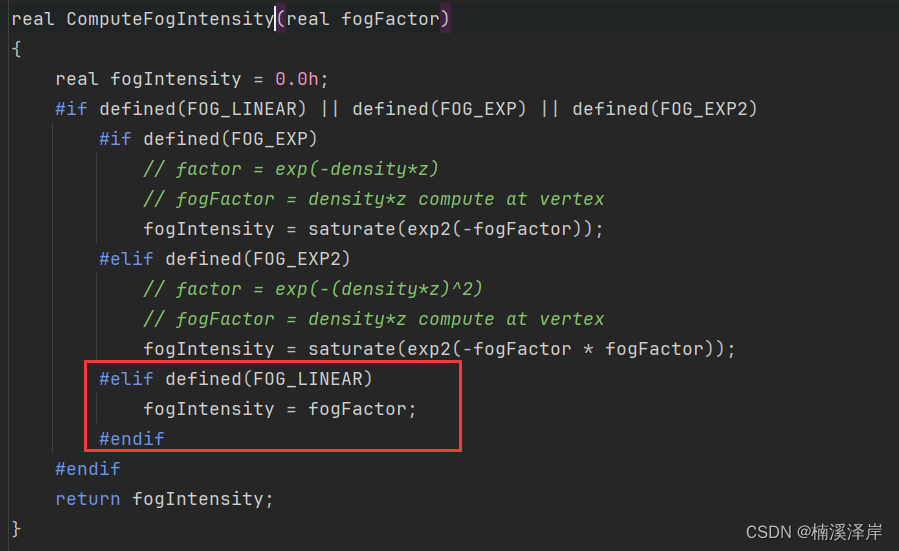
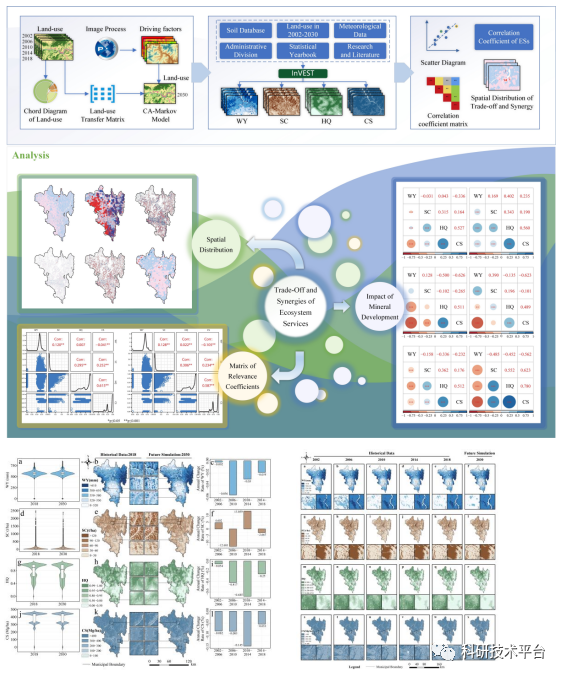
目录
- 1. 傅里叶级数
- 2.傅里叶变换
1. 傅里叶级数
功能:能把任意周期性函数展开成一系列正弦、余弦函数的和。
公式:
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos ( 2 π n x T ) + b n sin ( 2 π n x T ) ) 傅里叶系数 a n = 2 T ∫ x 0 x 0 + T f ( x ) ⋅ cos ( 2 π n x T ) d x , n ∈ { 0 } ⋃ N b n = 2 T ∫ x 0 x 0 + T f ( x ) ⋅ sin ( 2 π n x T ) d x , n ∈ N \begin{gathered} f(x)=\frac{a_0}2+\sum_{n=1}^{\infty}\left(a_n\cos(\frac{2\pi nx}T)+b_n\sin(\frac{2\pi nx}T)\right) \\ \text{傅里叶系数} \\ a_{n}=\frac{2}{T}\int_{x_{0}}^{x_{0}+T}f(x)\cdot\cos(\frac{2\pi nx}{T})dx,n\in\{0\}\bigcup\mathbb{N} \\ b_{n}={\frac{2}{T}}\int_{x_{0}}^{x_{0}+T}f(x)\cdot\sin({\frac{2\pi nx}{T}})dx,n\in\mathbb{N} \end{gathered} f(x)=2a0+n=1∑∞(ancos(T2πnx)+bnsin(T2πnx))傅里叶系数an=T2∫x0x0+Tf(x)⋅cos(T2πnx)dx,n∈{0}⋃Nbn=T2∫x0x0+Tf(x)⋅sin(T2πnx)dx,n∈N
比如下图的一个函数能够被一系列周期为2
π
\pi
π的正弦函数展开:
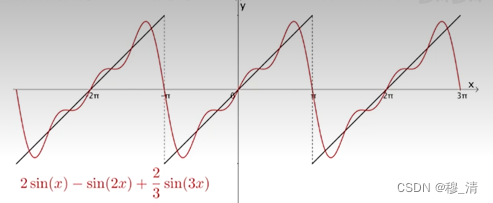
加加减减后周期仍是2
π
\pi
π,调整正弦、余弦函数前面的系数(振幅)就可以慢慢逼近原函数了。
下面我们尝试把周期变成更一般的T,则正弦、余弦函数可写成:
s
i
n
(
2
π
n
T
x
)
c
o
s
(
2
π
n
T
x
)
\begin{array}{l}sin(\frac{2\pi n}Tx)\\\\cos(\frac{2\pi n}Tx)\end{array}
sin(T2πnx)cos(T2πnx)
前面的系数( a n , b n a_n, b_n an,bn)我们可以通过几何的角度进行理解:
首先要有个先验知识就是正弦、余弦函数可以看成无限维的向量,并且两个向量的内积为0,即正弦余弦函数是正交的。
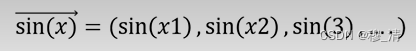
无限维向量内积:
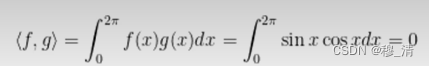
因此傅里叶变换可看成是由一组正交基构成的:

每个正交向量就是:{1,0,0},{0,cos(2pi n/T x),0},{0,0,sin(2pin/Tx)}
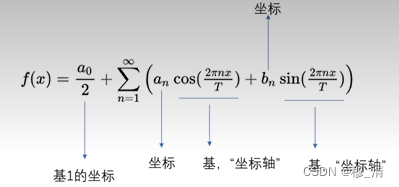
那么如何求系数呢 就是这些坐标:
例如:其中c1,c2是坐标
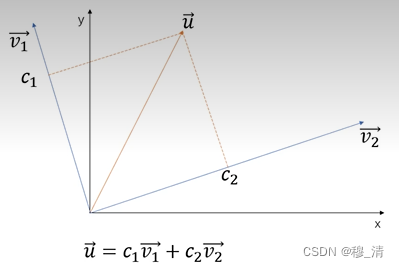
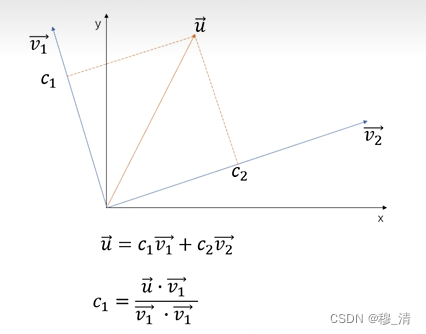
扩展到傅里叶:

bn类似的。
2.傅里叶变换
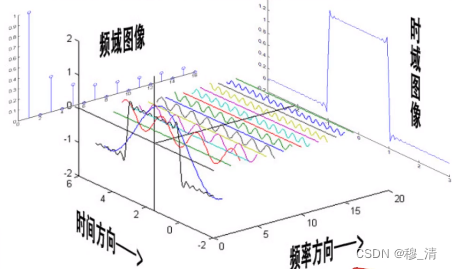
随着函数周期变大,频域上的点会越来越密集,若一个非周期函数,则频域图中的点连续:
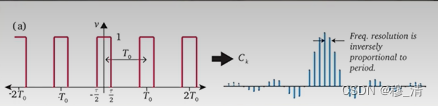
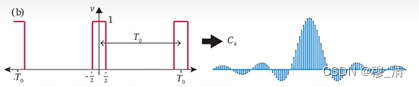
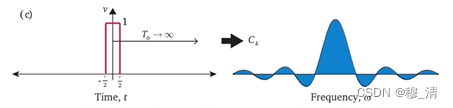
而傅里叶变换就是求出当周期无穷大时,对应的这个连续的频域图曲线。
首先把傅里叶级数用欧拉公式换一下:
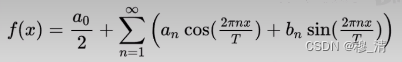
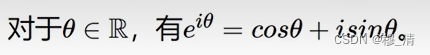


F(w)就是频域曲线。
另外还可以再改造一下,把前面系数移进去:
F ( w ) = ∫ − ∞ + ∞ f ( x ) ⋅ e − j 2 π w x d x F(w)=\int_{-\infty}^{+\infty}f(x)\cdot e^{-j2\pi wx}dx F(w)=∫−∞+∞f(x)⋅e−j2πwxdx
同理可得二维傅里叶变换:
F
(
u
,
v
)
=
∫
−
∞
+
∞
∫
−
∞
+
∞
f
(
x
,
y
)
⋅
e
−
j
2
π
(
u
x
+
v
y
)
d
x
d
y
F(u, v)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)\cdot e^{-j2\pi (ux+vy)}dxdy
F(u,v)=∫−∞+∞∫−∞+∞f(x,y)⋅e−j2π(ux+vy)dxdy
二维傅里叶反变换:
f
(
x
,
y
)
=
∫
−
∞
+
∞
∫
−
∞
+
∞
F
(
u
,
v
)
⋅
e
j
2
π
(
u
x
+
v
y
)
d
u
d
v
f(x, y)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}F(u,v)\cdot e^{j2\pi (ux+vy)}dudv
f(x,y)=∫−∞+∞∫−∞+∞F(u,v)⋅ej2π(ux+vy)dudv
二维离散傅里叶变换:
F
(
u
,
v
)
=
∑
m
=
0
M
−
1
∑
n
=
0
N
−
1
f
(
x
,
y
)
⋅
e
−
j
2
π
(
u
x
/
M
+
u
y
/
N
)
F(u, v) = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(x, y) \cdot e^{-j 2\pi(ux/M + uy/N)} \
F(u,v)=m=0∑M−1n=0∑N−1f(x,y)⋅e−j2π(ux/M+uy/N)
f ( x , y ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) ⋅ e j 2 π ( u x / M + u y / N ) \ f(x, y) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) \cdot e^{j 2\pi(ux/M + uy/N)} \ f(x,y)=MN1u=0∑M−1v=0∑N−1F(u,v)⋅ej2π(ux/M+uy/N)
- 小波变换
暂时放个链接在这小波变换
- 离散余弦变换
离散余弦变换其实就是傅里叶变换的实数部分
F ( u , v ) = λ ( u ) λ ( v ) ∑ x = 0 N 1 − 1 ∑ y = 0 N 2 − 1 f ( x , y ) cos ( π u 2 x + 1 2 N 1 ) cos ( π v 2 y + 1 2 N 2 ) λ ( ω ) = { 1 N , i f ω = 0 2 N , o t h e r w i s e \begin{aligned}F(u,v)&=\lambda(u)\lambda(v)\sum_{x=0}^{N_1-1}\sum_{y=0}^{N_2-1}f(x,y)\cos\left(\pi u\frac{2x+1}{2N_1}\right)\cos\left(\pi v\frac{2y+1}{2N_2}\right)\\\\\lambda(\omega)&=\begin{cases}\sqrt{\frac1N},&\mathrm{if~}\omega=0\\\sqrt{\frac2N},&\mathrm{otherwise}&\end{cases}\end{aligned} F(u,v)λ(ω)=λ(u)λ(v)x=0∑N1−1y=0∑N2−1f(x,y)cos(πu2N12x+1)cos(πv2N22y+1)=⎩ ⎨ ⎧N1,N2,if ω=0otherwise
f ( x , y ) = ∑ u = 0 N 1 − 1 ∑ v = 0 N 2 − 1 λ ( u ) λ ( v ) F ( u , v ) cos ( π u 2 x + 1 2 N 1 ) cos ( π v 2 y + 1 2 N 2 ) \begin{aligned}f(x,y) & =\sum_{u=0}^{N_1-1}\sum_{v=0}^{N_2-1}\lambda(u)\lambda(v)F(u,v)\cos\left(\pi u\frac{2x+1}{2N1}\right)\cos\left(\pi v\frac{2y+1}{2N2}\right)\end{aligned} f(x,y)=u=0∑N1−1v=0∑N2−1λ(u)λ(v)F(u,v)cos(πu2N12x+1)cos(πv2N22y+1)