序言

心若有阳光，你便会看见这个世界有那么多美好值得期待和向往。

决定开一个算法专栏，希望能帮助大家很好的了解算法。主要深入解析每个算法，从概念到示例。

我们一起努力，成为更好的自己！

今天第11讲，讲一下查找算法的—插值查找算法

一、基础介绍

查找算法是计算机科学中的一类算法，用于在数据集中寻找特定值或数据项。

其目标是确定数据是否存在于给定的数据结构中，并找到数据项的位置（索引）或其他相关信息。

不同的查找算法适用于不同类型的数据结构，数据有序性，以及数据规模。以下是一些常见的查找算法

以下是一些常见的查找算法及其应用场景：

• 布隆过滤器（Bloom Filter）：适用于判断一个元素是否存在于一个大规模的数据集中，时间复杂度为O(1)，但有一定的误判率。

• 二分查找（Binary Search）：适用于有序数组中查找元素，时间复杂度为O(log n)；

• 哈希表查找（Hash Table）：适用于快速查找和插入元素，时间复杂度为O(1)，但需要额外的存储空间；

• 线性查找（Linear Search）：适用于无序数组中查找元素，时间复杂度为O(n)；

• 插值查找（Interpolation Search）：适用于有序数组中查找元素，时间复杂度为O(log log n)，但是对于分布不均匀的数据集效果不佳；

• 斐波那契查找（Fibonacci Search）：适用于有序数组中查找元素，时间复杂度为O(log n)，但需要额外的存储空间；

• 树表查找（Tree Search）：适用于快速查找和插入元素，时间复杂度为O(log n)，但需要额外的存储空间；

• B树查找（B-Tree）：适用于大规模数据存储和查找，时间复杂度为O(log n)，但需要额外的存储空间；

一、算法介绍

1.1 原理介绍

插值查找是一种改良版的二分查找算法，其基本原理是根据要查找的值在有序数组中的大致位置进行估计，以此来缩小搜索范围，从而提高查找效率。

插值查找的核心思想是通过数据的分布情况来预测目标值的位置，从而更快地逼近目标。

特别适用于有序且均匀分布的数据集

插值查找的实现步骤

插值查找的实现步骤相对简单，主要包括以下几个步骤：

a. 计算插值位置

首先，通过插值公式计算目标值在数组中的估计位置：

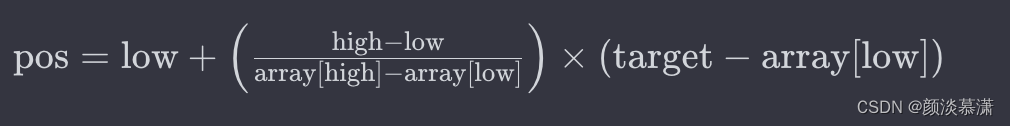
其中，low[low ]和 high[high]分别是数组的起始位置和结束位置，array[low] 和 array[high] 分别是对应位置的元素值。

b. 判断目标值位置

比较目标值与估计位置的大小关系，决定在左半部分还是右半部分继续查找。

c. 递归或迭代

根据比较结果，继续在选定的半部分进行插值查找，直到找到目标值或确定目标值不存在。

1.2 优缺点

优点：

• 适用于均匀分布的数据集： 插值查找在数据集均匀分布时效果更为显著，能够更准确地估计目标值的位置。

• 相对于二分查找的改进： 在某些情况下，插值查找的效率较二分查找更高，尤其是对于近似均匀分布的数据。

缺点：

• 对于不均匀分布的数据效果不佳： 当数据分布不均匀时，插值查找的性能可能较差，甚至不如二分查找。

• 可能导致溢出： 在计算插值位置时，由于分母可能为零，导致除法溢出的风险。

1.3 复杂度

插值查找的时间复杂度主要取决于查找的数据分布情况，但最坏情况下的时间复杂度仍然是 O(log n)。下面是插值查找的复杂度的详细解释：

1. 最好情况时间复杂度：O(1) 如果你运气好，目标元素恰好在数组的中间位置，此时插值查找的时间复杂度为常数级别，即 O(1)。这种情况下，插值查找的效率最高。

2. 平均情况时间复杂度：O(log log n) 到 O(log n) 在平均情况下，插值查找的时间复杂度在 O(log log n) 到 O(log n) 之间。这是因为插值查找适用于均匀分布的数据，能够更准确地估计目标值的位置。在每一步查找中，搜索范围都会迅速减半，类似于二分查找。

3. 最坏情况时间复杂度：O(n) 最坏情况下的时间复杂度为 O(n)，通常发生在数据分布不均匀的情况下。如果数据分布不均匀，插值查找可能会导致多次不必要的递归或迭代，使得时间复杂度增加。

总体来说，插值查找在数据分布较为均匀的情况下性能较好，但在不均匀分布的情况下可能退化为线性查找。

因此，在选择查找算法时，需要根据实际数据分布情况权衡算法的优缺点。插值查找的优势在于能够更好地适应均匀分布的数据，但在不确定数据分布情况时，二分查找等算法可能更稳定。

1.4 使用场景

插值查找适用于数据集较大且分布相对均匀的情况，例如在数字、日期等有序数据的查找中表现较好。

在这些场景下，插值查找能够更准确地估计目标值的位置，从而提高查找效率。

1.5 拓展

可以用更简单的语言来解释插值查找算法的原理。

比方说你在一本按照字母顺序排列的电话簿中找人的电话号码。

1. 常规查找（比如二分查找）： 你会打开电话簿的中间，看这个名字是在中间的上面还是下面。然后根据比较的结果，再在剩下的一半中间找。

2. 插值查找： 插值查找不是简单地在中间找，而是像“猜谜底”一样，通过一些估算，去猜测名字更可能在哪。比如，如果你要找的名字离电话簿的开头近，插值查找就猜测他可能在电话簿的前面。然后，你再根据这个猜测去找。

为什么这样做更快呢？🤔

假如电话簿中的名字是均匀分布的，你可以更准确地猜测名字的位置。就好比你知道字母表中的字母是均匀分布的，你可以更快地找到某个字母的位置。

总的来说，插值查找是一种更智能的查找方法，通过估算目标的位置，可以更快地找到你要找的东西。

二、代码实现

2.1 Java代码实现

2.1.1 代码示例

public class InterpolationSearch {

    public static int interpolationSearch(int[] array, int target) {
        int low = 0;
        int high = array.length - 1;

        while (low <= high && target >= array[low] && target <= array[high]) {
            // 使用插值公式计算估计位置
            int pos = low + ((target - array[low]) * (high - low)) / (array[high] - array[low]);

            if (array[pos] == target) {
                return pos; // 找到目标值，返回位置
            } else if (array[pos] < target) {
                low = pos + 1; // 在右半部分查找
            } else {
                high = pos - 1; // 在左半部分查找
            }
        }

        return -1; // 目标值不存在
    }

    public static void main(String[] args) {
        int[] array = {1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20};
        int target = 12;

        int result = interpolationSearch(array, target);

        if (result != -1) {
            System.out.println("目标值 " + target + " 在数组中的位置是：" + result);
        } else {
            System.out.println("目标值 " + target + " 未在数组中找到。");
        }
    }
}

2.1.2 代码详解

1. interpolationSearch 方法是插值查找的实现，接受一个有序数组 array 和目标值 target 作为参数。

2. low 和 high 分别表示数组的起始和结束位置。

3. 使用 while 循环进行查找，确保目标值在数组范围内。

4. 插值公式计算估计位置 pos，并根据与目标值的比较确定在左半部分还是右半部分继续查找。

5. 如果找到目标值，返回它在数组中的位置；如果未找到，返回 -1。

6. main 方法演示了如何使用插值查找算法来查找目标值在数组中的位置。

2.1.3 运行结果

目标值 12 在数组中的位置是：6

• 目标值 12 在给定的有序数组 {1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20} 中的位置是索引 6。

• 因此，输出结果表示目标值 12 在数组中的位置为 6。

2.2 Python代码实现

2.2.1 代码示例

def interpolation_search(array, target):
    low = 0
    high = len(array) - 1

    while low <= high and array[low] <= target <= array[high]:
        # 使用插值公式计算估计位置
        pos = low + ((target - array[low]) * (high - low)) // (array[high] - array[low])

        if array[pos] == target:
            return pos  # 找到目标值，返回位置
        elif array[pos] < target:
            low = pos + 1  # 在右半部分查找
        else:
            high = pos - 1  # 在左半部分查找

    return -1  # 目标值不存在


# 示例用法
array = [1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
target = 12

result = interpolation_search(array, target)

if result != -1:
    print(f"目标值 {target} 在数组中的位置是：{result}")
else:
    print(f"目标值 {target} 未在数组中找到。")

2.2.2 代码详解

1. interpolation_search 函数是插值查找的实现，接受一个有序数组 array 和目标值 target 作为参数。

2. low 和 high 分别表示数组的起始和结束位置。

3. 使用 while 循环进行查找，确保目标值在数组范围内。

4. 插值公式计算估计位置 pos，并根据与目标值的比较确定在左半部分还是右半部分继续查找。

5. 如果找到目标值，返回它在数组中的位置；如果未找到，返回 -1。

6. 示例用法中演示了如何使用插值查找算法来查找目标值在数组中的位置。

2.2.3 运行结果

运行这段代码将输出：

目标值 12 在数组中的位置是：6

这表示目标值 12 在给定的有序数组 [1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20] 中的位置是索引 6。

好啦，今天就到这里啦，下期见喽~~🙉