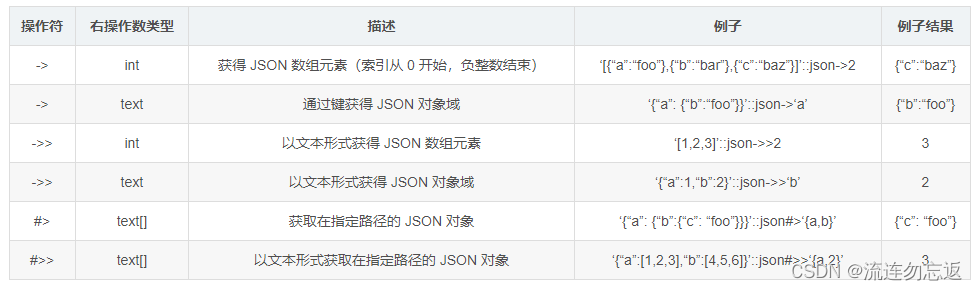
西尔维斯特方程(Sylvester equation)官方求解有问题
- 1. 西尔维斯特方程(Sylvester equation)
- 1.1 以上所有矩阵都是2x2矩阵的演算形式
- 2. 官方求解Sylvester方程-错误
- 2.1 官方求解形式
- 2.2 2x2矩阵举例
- 3. Nicolas Andreff作者文章On-line Hand-Eye Calibration-错误
- 3.1 2x2矩阵举例证明是错误的
- 4. 求解Sylvester方程的正确形式
- 4.1 2x2矩阵举例
1. 西尔维斯特方程(Sylvester equation)
如下拷贝的百度百科
西尔维斯特方程(Sylvester equation)是控制理论中的矩阵方程,形式如下:
A
X
+
X
B
=
C
AX+XB=C
AX+XB=C
其中A、B及C是已知的矩阵,问题是要找出符合条件的X。其中所有矩阵的系数都是复数。
为了要使上述方程成立,矩阵的行和列需要满足一定条件,A和B都要是方阵,大小分别是n和m,而X和C要是n行m列的矩阵,n和m也可以相等,四个矩阵都是大小相同的方阵。
西尔维斯特方程有唯一解X的充分必要条件是A和-B没有共同的特征值。
1.1 以上所有矩阵都是2x2矩阵的演算形式
A
X
+
X
B
=
[
a
1
a
2
a
3
a
4
]
[
x
1
x
2
x
3
x
4
]
+
[
x
1
x
2
x
3
x
4
]
[
b
1
b
2
b
3
b
4
]
=
[
(
a
1
+
b
1
)
x
1
+
b
3
x
2
+
a
2
x
3
+
0
x
4
b
2
x
1
+
(
a
1
+
b
4
)
x
2
+
0
x
3
+
a
2
x
4
a
3
x
1
+
0
x
2
+
(
a
4
+
b
1
)
x
3
+
b
3
x
4
0
x
1
+
a
3
x
2
+
b
2
x
3
+
(
a
4
+
b
4
)
x
4
]
=
[
c
1
c
2
c
3
c
4
]
AX+XB=\begin{bmatrix} a_1 & a_2\\ a_3 & a_4 \end{bmatrix}\begin{bmatrix} x_1 & x_2\\ x_3 & x_4 \end{bmatrix}+\begin{bmatrix} x_1 & x_2\\ x_3 & x_4 \end{bmatrix}\begin{bmatrix} b_1 & b_2\\ b_3 & b_4 \end{bmatrix}\\ =\begin{bmatrix} (a_1+b_1)x_1+b_3x_2+a_2x_3+0x_4 & b_2x_1+(a_1+b_4)x_2+0x_3+a_2x_4\\ a_3x_1+0x_2+(a_4+b_1)x_3+b_3x_4 & 0x_1+a_3x_2+b_2x_3+(a_4+b_4)x_4 \end{bmatrix} =\begin{bmatrix} c_1 & c_2\\ c_3 & c_4 \end{bmatrix}
AX+XB=[a1a3a2a4][x1x3x2x4]+[x1x3x2x4][b1b3b2b4]=[(a1+b1)x1+b3x2+a2x3+0x4a3x1+0x2+(a4+b1)x3+b3x4b2x1+(a1+b4)x2+0x3+a2x40x1+a3x2+b2x3+(a4+b4)x4]=[c1c3c2c4]
将以上算式推导中的C矩阵如下展开:
[
c
1
c
2
c
3
c
4
]
⇒
[
c
1
c
2
c
3
c
4
]
\begin{bmatrix} c_1 & c_2\\ c_3 & c_4 \end{bmatrix}\Rightarrow\begin{bmatrix} c_1\\ c_2\\ c_3\\ c_4 \end{bmatrix}
[c1c3c2c4]⇒
c1c2c3c4
则以上算式推导,可演变为如下形式:
[
a
1
+
b
1
b
3
a
2
0
b
2
a
1
+
b
4
0
a
2
a
3
0
a
4
+
b
1
b
3
0
a
3
b
2
a
4
+
b
4
]
[
x
1
x
2
x
3
x
4
]
=
[
c
1
c
2
c
3
c
4
]
\begin{bmatrix} a_1+b_1 & b_3 & a_2 & 0\\ b_2 & a_1+b_4 & 0 & a_2\\ a_3 & 0 & a_4+b_1& b_3\\ 0 & a_3 & b_2 & a_4+b_4 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}=\begin{bmatrix} c_1\\ c_2\\ c_3\\ c_4 \end{bmatrix}
a1+b1b2a30b3a1+b40a3a20a4+b1b20a2b3a4+b4
x1x2x3x4
=
c1c2c3c4
2. 官方求解Sylvester方程-错误
2.1 官方求解形式
( I ⨂ A + B T ⨂ I ) v e c ( X ) = v e c ( C ) (I\bigotimes A + B^T\bigotimes I)vec(X) = vec(C) (I⨂A+BT⨂I)vec(X)=vec(C)
2.2 2x2矩阵举例
( I ⨂ A + B T ⨂ I ) v e c ( X ) = ( [ 1 0 0 1 ] ⨂ [ a 1 a 2 a 3 a 4 ] + [ b 1 b 3 b 2 b 4 ] ⨂ [ 1 0 0 1 ] ) v e c ( X ) = ( [ a 1 a 2 0 0 a 3 a 4 0 0 0 0 a 1 a 2 0 0 a 3 a 4 ] + [ b 1 0 b 3 0 0 b 1 0 b 3 b 2 0 b 4 0 0 b 2 0 b 4 ] ) [ x 1 x 2 x 3 x 4 ] = [ a 1 + b 1 a 2 b 3 0 a 3 a 4 + b 1 0 b 3 b 2 0 a 1 + b 4 a 2 0 b 2 a 3 a 4 + b 4 ] [ x 1 x 2 x 3 x 4 ] (I \bigotimes A + B^T \bigotimes I )vec(X)= (\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \bigotimes \begin{bmatrix} a_1 & a_2\\ a_3 & a_4 \end{bmatrix}+ \begin{bmatrix} b_1 & b_3\\ b_2 & b_4 \end{bmatrix} \bigotimes \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix})vec(X) \\ =(\begin{bmatrix} a_1 & a_2 & 0 & 0\\ a_3 & a_4 & 0 & 0\\ 0 & 0 & a_1& a_2\\ 0 & 0 & a_3 & a_4 \end{bmatrix} + \begin{bmatrix} b_1 & 0 & b_3 & 0\\ 0 & b_1 & 0 & b_3\\ b_2 & 0 & b_4& 0\\ 0 & b_2 & 0 & b_4 \end{bmatrix}) \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix} \\ =\begin{bmatrix} a_1+b_1 & a_2 & b_3 & 0\\ a_3 & a_4+b_1 & 0 & b_3\\ b_2 & 0 & a_1+b_4& a_2\\ 0 & b_2 & a_3 & a_4+b_4 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix} (I⨂A+BT⨂I)vec(X)=([1001]⨂[a1a3a2a4]+[b1b2b3b4]⨂[1001])vec(X)=( a1a300a2a40000a1a300a2a4 + b10b200b10b2b30b400b30b4 ) x1x2x3x4 = a1+b1a3b20a2a4+b10b2b30a1+b4a30b3a2a4+b4 x1x2x3x4
最后矩阵计算形式变为
[
a
1
+
b
1
a
2
b
3
0
a
3
a
4
+
b
1
0
b
3
b
2
0
a
1
+
b
4
a
2
0
b
2
a
3
a
4
+
b
4
]
[
x
1
x
2
x
3
x
4
]
=
[
c
1
c
2
c
3
c
4
]
\begin{bmatrix} a_1+b_1 & a_2 & b_3 & 0\\ a_3 & a_4+b_1 & 0 & b_3\\ b_2 & 0 & a_1+b_4& a_2\\ 0 & b_2 & a_3 & a_4+b_4 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}=\begin{bmatrix} c_1\\ c_2\\ c_3\\ c_4 \end{bmatrix}
a1+b1a3b20a2a4+b10b2b30a1+b4a30b3a2a4+b4
x1x2x3x4
=
c1c2c3c4
和1.1章节正常矩阵展开,相比较,可以看出:
官方求解形式是错误的!!!
3. Nicolas Andreff作者文章On-line Hand-Eye Calibration-错误
Nicolas Andreff作者在文章《On-line Hand-Eye Calibration》中提到Sylvester方程,修改为线性系统方程,也是错误的。具体形式如下:

3.1 2x2矩阵举例证明是错误的
4. 求解Sylvester方程的正确形式
( A ⨂ I + I ⨂ B T ) v e c ( X ) = v e c ( C ) (A\bigotimes I + I\bigotimes B^T)vec(X) = vec(C) (A⨂I+I⨂BT)vec(X)=vec(C)
4.1 2x2矩阵举例
(
A
⨂
I
+
I
⨂
B
T
)
v
e
c
(
X
)
=
(
[
a
1
a
2
a
3
a
4
]
⨂
[
1
0
0
1
]
+
[
1
0
0
1
]
⨂
[
b
1
b
3
b
2
b
4
]
)
v
e
c
(
X
)
=
(
[
a
1
0
a
2
0
0
a
1
0
a
2
a
3
0
a
4
0
0
a
3
0
a
4
]
+
[
b
1
b
3
0
0
b
2
b
4
0
0
0
0
b
1
b
3
0
0
b
2
b
4
]
)
[
x
1
x
2
x
3
x
4
]
=
[
a
1
+
b
1
b
3
a
2
0
b
2
a
1
+
b
4
0
a
2
a
3
0
a
4
+
b
1
b
3
0
a
3
b
2
a
4
+
b
4
]
[
x
1
x
2
x
3
x
4
]
=
[
c
1
c
2
c
3
c
4
]
(A\bigotimes I + I\bigotimes B^T)vec(X)= (\begin{bmatrix} a_1 & a_2\\ a_3 & a_4 \end{bmatrix} \bigotimes \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}+ \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \bigotimes \begin{bmatrix} b_1 & b_3\\ b_2 & b_4 \end{bmatrix})vec(X) \\ =(\begin{bmatrix} a_1 & 0 & a_2 & 0\\ 0 & a_1 & 0 & a_2\\ a_3 & 0 & a_4& 0\\ 0 & a_3 & 0 & a_4 \end{bmatrix} + \begin{bmatrix} b_1 & b_3 & 0 & 0\\ b_2 & b_4 & 0 & 0\\ 0 & 0 & b_1& b_3\\ 0 & 0 & b_2 & b_4 \end{bmatrix}) \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix} \\ =\begin{bmatrix} a_1+b_1 & b_3 & a_2 & 0\\ b_2 & a_1+b_4 & 0 & a_2\\ a_3 & 0 & a_4+b_1& b_3\\ 0 & a_3 & b_2 & a_4+b_4 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}=\begin{bmatrix} c_1\\ c_2\\ c_3\\ c_4 \end{bmatrix}
(A⨂I+I⨂BT)vec(X)=([a1a3a2a4]⨂[1001]+[1001]⨂[b1b2b3b4])vec(X)=(
a10a300a10a3a20a400a20a4
+
b1b200b3b40000b1b200b3b4
)
x1x2x3x4
=
a1+b1b2a30b3a1+b40a3a20a4+b1b20a2b3a4+b4
x1x2x3x4
=
c1c2c3c4
和1.1章节的最后结果是一致的。