动态规划：解决复杂问题的魔法武器

🐳今日良言：天会晴，心会暖

🐉一、什么是动态规划

🐉二、如何使用动态规划

🐉三、典型例题

🐳今日良言：天会晴，心会暖

🐉一、什么是动态规划

动态规划（Dynamic Programming，简称DP）是一种在数学、管理科学、计算机科学、经济学动态规划（Dynamic Programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。它是一种利用重复子问题的性质来求解复杂问题的算法思想。

上述只是对于动态规划进行一个官方解释，接下来博主介绍一下动态规划的基本思想：

将一个复杂的问题分解成一系列相互重叠的子问题，然后将子问题的解决方案组合起来，形成整个问题的解决方案。

🐉二、如何使用动态规划

上述简单的了解了动态规划之后，是不是一头雾水？不要着急，继续往下看，待博主细细道来。

动态规划通常用于优化一下问题，比如：最短路径、最长公共子序列、背包问题等。

使用动态规划解决问题的步骤一般都是固定的，一般是如下五个解决步骤：

1.状态表示

2.状态转移方程

3.初始化

4.填表顺序

5.返回值

接下来，我将依次介绍这五个步骤的内容。

1.状态表示

在解决动态规划问题的时候，一般会创建一个dp表（一维数组或者二维数组），这里先用简单的一维数组。

解决动态规划就是将这个dp表中的数据填满，其中，状态表示就是dp表中每个位置的值代表的含义。

大多数对于状态表示的解释都比较晦涩难懂，这里感性的理解成博主上述表达的意思，通过大量做题来深刻理解状态表示。

知道了状态表示是什么，就需要考虑状态表示如何得到？

主要有以下三个方向：

1）题目要求

一般题目有些题目会给出状态表示

2）经验 + 题目要求

通过大量的做题积累经验，水到而渠成。

3）分析子问题的过程中，发现重复的子问题。

将这个重复的子问题抽象成状态表示。

通过一道最简单的动态规划入门例题来解释上述比较抽象的概念：

在这道题中，可以直接根据题目要求（返回第n个泰波那契数）来得到状态表示。在dp表中，dp[0] 表示第一个泰波那契数，dp[1]表示第二个泰波那契数......dp[i]表示第i个泰波那契数。由此，就可以得到状态表示：

dp[i]表示：第 i 个泰波那契数的值。

状态表示是解决动态规划问题的第一步，至关重要，与状态转移方程相比的重要程度不遑多让，如果连状态表示都找不出，整个状态转移方程就无法解决了。

2.状态转移方程

之前接触过动态规划问题或者做过相关例题的老铁应该知道状态转移方程的重要性，状态转移方程决定了如何解决动态规划问题，对于状态转移方程的寻找可谓是至关重要。

对于状态转移方程的解释可以简单理解一下：

状态转移方程就是 dp[i] 等于什么

以上述例题为例，这里已经告诉了dp[i] 等于什么：

dp[i] = dp[i-3] + dp[i-2] + dp[i-1]

上述这个公式就是状态转移方程

上述是解决动态规划问题的两个核心步骤，接下来介绍剩余的三个细节步骤。

3.初始化

“保证填dp表的时候不越界”

根据状态转移方程来进行dp表中的一些位置的初始化，避免发生越界错误。这个小步骤需要和状态转移方程结合来进行。

对于上述状态转移方程： dp[i] = dp[i-3] + dp[i-2] + dp[i-1]

如果通过这个状态转移方程填dp[0] 位置，就会出现 dp[0] = dp[-3] + dp[-2] + dp[-1] ，显然发生了越界错误，因此，在填dp表的时候需要先对表中的一些位置进行初始化。

对于这道例题来说，需要初始化的位置有前三个（dp[0] dp[1] dp[2]），并且具体初始化的值在题目中已经给出，直接初始化dp[0] = 0，dp[1] = dp[2] = 1

4.填表顺序

“为了填写当前状态的时候，所需要的状态已经计算过了”

以上面的例题为例，在dp表中，前三个位置已经初始化了，此时，如果博主想要填dp[4]这个位置，需要依赖前三个位置:dp[1] dp[2] dp[3]

但是dp[3] 还没有进行填表，因此需要先填dp[3] 然后再填dp[4],由此可以得到填这个dp表的顺序是：从左到右。并且开始填表的位置是dp[3].

5.返回值

“题目要求 + 状态表示”

以上面的例题来看，题目要求：返回第n个泰波那契数的值。状态表示dp[i]：第i个泰波那契数的值。因此，这道题目就返回dp[n] 的值即可。

上述五个步骤就是使用动态规划解决问题的步骤，这五个步骤需要频繁且大量的练习动态规划题目，通过大量的经验来加深理解。

对于动态规划问题编写代码的顺序一般也可以分五个步骤：

1.避免越界

2.创建dp表

3.初始化

4.填表

5.返回值

通过解决上述例题的代码来加深理解

class Solution {
    public int tribonacci(int n) {
        // 1.避免越界
        if (n == 0 || n == 1) {
            return n;
        }
        // 2.创建dp表
        // 由于要求第n个位置，因此创建n+1大小的数组
        int[] dp = new int[n+1];
        // 3.初始化
        // 初始化前三个位置
        dp[0] = 0;dp[1] = dp[2] = 1;
        // 4.填表
        // 从dp[3] 位置开始填表
        for (int i = 3; i <= n;i++) {
            dp[i] = dp[i-3] + dp[i-2] + dp[i-1];
        }
        // 5.返回值
        // 返回dp[n]
        return dp[n];
    }
}

以上解释解决一道动态规划问题的基本流程，刚接触动态规划问题的老铁如果不知道如何下手，可以先按照上述流程写一个模版来尝试解决问题。

接下来，博主将选择几道比较经典的动态规划问题来熟悉上述流程。

🐉三、典型例题

1.路径问题

路径问题是动态规划比较经典的例题，如下链接：

LCR 098. 不同路径 - 力扣（LeetCode）

这里虽然是二维数组问题，但是上述解决动态规划问题的步骤依旧适用。

1.状态表示

状态表示是找dp表中每个位置的值代表的含义，根据题目要求可知：dp表中存的是到达某个位置的不同路径数目，由于是二维数组，每个位置需要通过横纵坐标组合表示，因此，可以得到：dp[i][j] 表示：到达i j 位置的不同路径的数目。

上述就是状态表示。

2.状态转移方程

找状态转移方程就是找dp[i][j] 等于什么，分析题目，对于每一个位置来说：可以通过机器人所处的上一个位置往下一步，或者左边一个位置往右一步可以得到。

也就是说: dp[i][j] 这个位置可以从dp[i-1][j] 往下一步或者 dp[i][j-1] 这个位置往右一步。

题目要求总共的路径条数，因此，状态转移方程就是：dp[i][j] = dp[i-1][j] + dp[i][j-1]

3.初始化

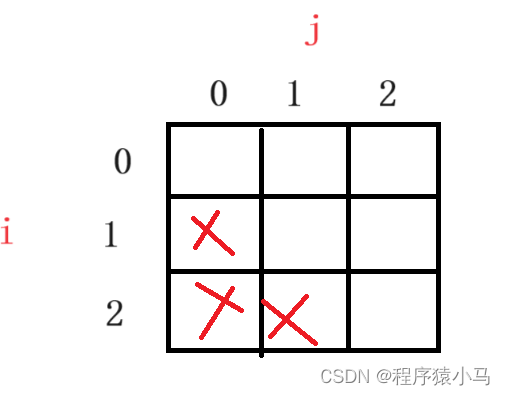
初始化是为了避免越界，在初始化时，可以根据状态转移方程来进行初始化，在状态转移方程中，假设要求dp[0][0]，根据状态转移方程: dp[0][0] = dp[-1][0] + dp[0][-1] 会发现越界问题，为了避免越界问题，在填二维dp表的时候，可以采取的策略是多开一行和一列。

假设题目给的是一个 5 X 4 的网格，需要创建出一个 5X 4的如下dp表：

但是 5 X 4 的dp表在初始化的时候会发生越界访问，因此采取多开一行和一列的策略：创建一个 6 X 5 的dp表：

对于这个dp表来说，需要填的部分是图中黑色网格，红色的不用填，也就是实际开始填的位置是dp[1][1]，但是dp[1][1] 依赖dp[1][0] 和 dp[0][1] 这两个位置，由于机器人到达第一个位置，它的路径只有一条，因此，将dp[1][0] 和 dp[0][1] 其中的一个值初始化为1，来进行填表。假设dp[0][1] = 1:

上述就是初始化操作。

4.填表顺序

假设现在要填 dp[3][4] 这个位置，根据状态转移方程来考虑，需要先填dp[2][4] 和dp[3][3] 位置，因此，可以得出填表顺序是：从左到右并且从上往下。

5.返回值

根据题目要求，需要返回到达[m-1][n-1] 位置的不同路径数目，结合状态表示（dp[i][j]表示到达i j位置的不同路径数目），应该返回dp[m-1][n-1]。但是，由于dp表多开了一行和一列，最终返回的结果应该是dp[m][n]。

上述就是整个解决此道动态规划的分析流程，编写代码如下：
class Solution {
    public int uniquePaths(int m, int n) {
        // 1.创建dp表
        // 需要多开一行和一列
        int[][] dp = new int[m+1][n+1];
        // 2.初始化
        // 需要初始化dp[0][1] 或者 dp[1][0]
        dp[0][1] = 1;
        // 3.填表
        //   从 1 1 位置开始填
        for(int i = 1; i <= m;i++) {
            for (int j = 1; j <= n;j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        // 4.返回值
        return dp[m][n];
    }
}
以上就是路径问题一道比较经典的例题解法。

2.简单多状态问题

如下例题：

面试题 17.16. 按摩师 - 力扣（LeetCode）

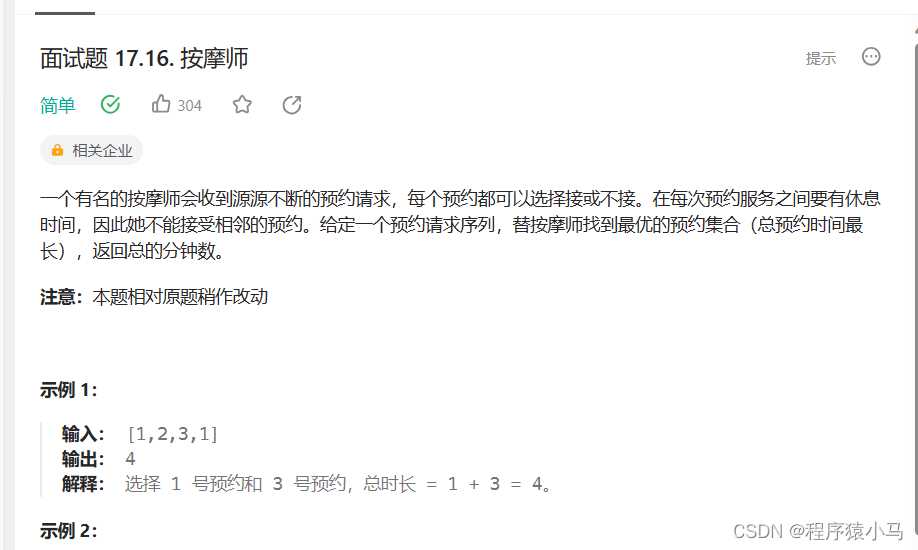
接下来，使用五步法来解决这道例题：

1.状态表示

分析题目要求：给定的数组表示预约时间，通过选择这个数组中的一些元素来获得最大的总时长。对于实例1（【1,2,3,4】）来说，可以先选择第一个位置，然后第二个位置不能选，再选择第三个位置，第四个位置不选，这样最终得到的时长是最大的。

上述是分析题目要求的，接下来找状态表示：

根据经验+题目要求，dp表中存的是选择每个位置的最长预约时间，对于该题来说，状态表示（dp[i]）是：选择到 i 位置的时候，此时的最长预约时间。

状态表示找到了，但是需要注意，在题目中有这样一个要求：

对于每个位置来说，按摩师都有两种选择：接或者不接。因此可以划分出两个状态，对于这种情况，我们常用的策略是：根据状态的数量来创建dp表的数目。对于这道题来说，可以创建两张dp表：

f[i] 表示：选择到 i 位置的时候，选nums[i],此时的最长预约时间。

g[i]表示：选择到 i 位置的时候，不选nums[i],此时的最长预约时间。

2.状态转移方程

状态转移方程就是找dp[i]等于什么，套用到这道题，也就是找f[i] 和 g[i] 等于什么。

f[i] 表示的是到 i 位置时，选nums[i] 这个预约时间，此时的最长预约时间。那么i - 1 这个位置就不能选择了，因此，f[i] = g[i-1] + nums[i] (这里的意思是当前f[i] 的值，就等于前面i-1位置不选择的最长预约时间 + 当前nums[i] )

g[i] 表示的是到i - 1 位置时，不选nums[i]这个预约时间，此时的最长预约时间，那么i - 1这个位置就有两种选择：选择 i - 1 或者不选 i -1，因此，g[i] = f[i-1] （不选i位置并且选择i-1位置的最长预约时间）或者 g[i] = g[i-1] (不选i位置并且不选i-1位置的最长预约时间)

由于要求最长预约时间，也就是上述两种情况的最大值，因此：

g[i] = Math.max(f[i-1],g[i-1])

3.初始化

根据状态转移方程来进行初始化，在状态转移方程中，出现了 i - 1 就需要考虑是否越界，通常的做法是给数组多开一个位置，但是这道题由于初始化比较简单，所以就不需要多开一个位置，直接根据状态转移方程初始化即可。

f[0] 表示的是选择到0位置，选nums[0],此时的最长预约时间，则f[0] = nums[0]

g[0] 表示的是选择到0为止，不选nums[0]，此时的最长预约时间,则g[0] = 0

后续填表的时候，从1下标开始填即可。

4.填表顺序

由于有两张dp表，又因为这两张dp表直接有依赖关系，因此需要两张表一起填。

假设要填f[3] 和 g[3] 这两个位置，那么g[2] 和 f[2] 这两个位置需要先填，因此，填表顺序就是：从左到右且两表同时填。

5.返回值

题目要求返回的是最长的预约时间，由于有两张表，因此需要返回两张表最后一个位置的较大值（最后一个位置选择或者不选择有两种情况，需要求这两种情况的最大值）。

上述就是整个解决此道动态规划的分析流程，编写代码如下：
class Solution {
    public int massage(int[] nums) {
        int n = nums.length;
        if (n == 0) return 0; 
        // 1.创建dp表
        // 两张表
        int[] f = new int[n];
        int[] g = new int[n];
        // 2.初始化
        f[0] = nums[0];
        g[0] = 0;// 表中数据默认就是0
        // 3.填表
        // 从1下标开始填，同时填
        for (int i = 1; i < n;i++) {
            // 选择i位置预约时间
            f[i] = g[i-1] + nums[i];
            // 不选择i位置预约时间
            g[i] = Math.max(g[i-1],f[i-1]);
        } 
        // 4.返回值
        return Math.max(f[n-1],g[n-1]);
    }
}
以上就是接这道例题的整体思路。

其实也可以只创建一个dp表来求解这个问题，但是需要注意的是：一定要区分不同的状态，也就是每个位置选择或者不选择。以下是解法，需要的老铁可以结合注释来理解：
class Solution {
    public int massage(int[] nums) {
        int n = nums.length;
        if (n == 0) return 0; 
        // 1.创建dp 表
        // 多开两个位置
        int[] dp = new int[n+2];
        // 2.初始化
        // 不同初始化
        // 3.填表
        // 从第2个下标开始，从左到右
        for (int i = 2; i < n+2;i++) {
            // 先选择当前i位置的预约时间（由于多开了两个位置，注意原来nums数组的映射）
            // 选择了当前i位置，则i-1位置就不能选择了,则i-2位置可以选
            dp[i] = dp[i-2] + nums[i-2];
            // 不选当前i位置的预约时间，和上面的值求个最大值就是当前dp[i]的最终值
            dp[i] = Math.max(dp[i-1],dp[i]);
        }
        return dp[n+1];
    }
}

3.子数组系列问题

上例题：53. 最大子数组和 - 力扣（LeetCode）

接下来，使用五步法来解决这道例题：

1.状态表示

先根据题目分析：首先，需要清楚什么是子数组，题目中已经告诉我们，子数组是数组中的一个“连续”部分，也就是说，选取的一些元素，这些元素的下标是连续的，在实例1中可以看出，从4开始到1的这部分子数组的和是最大的，其余的都比其小。

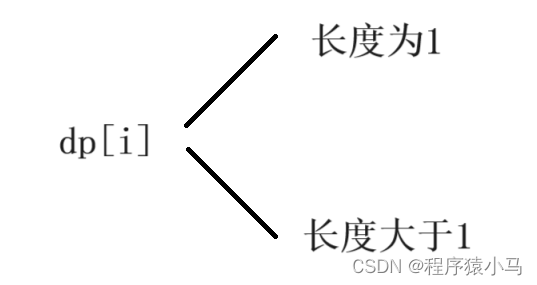
分析完题目，找状态表示(dp[i])，dp[i] 表示的是dp表中每个位置的值代表的含义，在这道题中，需要找出整个数组中所有连续子数组中的最大和，因此，dp[i] 表示：以i位置元素结尾的所有连续子数组中最大的和。

2.状态转移方程

状态转移方程就是找dp[i] 等于什么，如下图：

要求dp[i] 就是找，以dp[i] 结尾的所有连续子数组中的最大和，对于以i位置结尾的所有连续自子数组，有如下这些（也就是i下标元素和之前的元素组合，但是要求必须是连续的）：

也就是在这些所有连续子数组中找到和最大的。

对于上述子数组来说，可以划分成两种：一种是长度为1，也就是i位置元素自己，一种是长度大于1，也就是i位置元素和以i-1位置为结尾的连续子数组的最大和（也就是dp[i-1]）进行相加。对于这两种情况求最大值即可。

综上，dp[i] = Math.max(nums[i],nums[i] + dp[i-1])

3.初始化

进行初始化的时候，需要结合状态转移方程，在状态转移方程中出现了 i-1 ，此时就可以通过多开一个空间来避免越界，假设原来需要开辟的总长度是4，现在开辟5个空间，为了避免越界，填表的时候，从下标为1的位置开始填即可，新增的第一个位置的值为0即可，这样对后续填表就无影响。

由于多开了一个空间，需要注意和原数组的下标映射关系。

4.填表顺序

如果要求以4结尾的所有连续子数组的最大和，就需要知道以3结尾的连续子数组的最大和，因此，填表顺序就是：从左到右

5.返回值

这道题目最终的返回值是整个数组中所有连续子数组的最大和，dp表中存的是以某个位置为结尾的所有连续子数组的最大和，因此，可能最大值是在dp表中间存着，也可能是在开头或者结尾... 所以，最后遍历一次dp表（或者在填表的时候记录最大值最终返回）即可得到最终结果。

上述就是整个解决此道动态规划的分析流程，编写代码如下：
class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        // 1.创建dp表
        // 多开1个空间
        int[] dp = new int[n+1];
        // 2.初始化
        // 无需初始化
        // 3.填表
        // 从左到右，从1下标开始填（注意下标映射）
        for (int i = 1; i <= n;i++) {
            dp[i] = Math.max(nums[i-1],dp[i-1] + nums[i-1]);
        }
        // 4.返回值
        // 需要遍历dp表,还是从1下标开始
        int ret = Integer.MIN_VALUE;
        for(int i = 1;i <= n;i++) {
            ret = Math.max(ret,dp[i]);
        }
        return ret;
    }
}
以上就是子数组系列问题一道比较经典的例题解法。

4.子序列问题

子序列问题也是比较经典的动态规划题型，这里需要区分子序列和子数组的，组成子序列的一些元素的下标是可以不连续的，而组成子数组的一些元素的下标要求是连续的。

例题：300. 最长递增子序列 - 力扣（LeetCode）

1.状态表示

“经验 + 题目要求”

根据题目分析问题：要求找到给定数组中“最长严格递增子序列的长度”，也就是找到所有递增子序列中最长的长度。那么，dp表中就存的是：以某个位置为结尾的所有子序列中，最长递增子序列的长度，所以，状态表示（dp[i]）:以i位置结尾的所有子序列中，最长递增子序列长度。

2.状态转移方程

“找dp[i] 等于什么”

对于子序列问题，处理方式和子数组问题相似，都是以 i 位置为结尾分情况讨论：

i 位置自己的长度为1是一种情况，让 i 位置元素跟在 [0,i-1] 这个区间内的子序列的后面又是一种情况，因此dp[i] 就有两种情况：

对于长度大于1这种情况，有一个前提：

必须保证 i 位置选择要比前面的子序列的值要大。假设 j 是[0,i-1] 区间某个下标(0 <= j <= i-1)，那么想要 i 位置的元素跟在 j 位置的元素后面，就要求 nums[j] < nums[i]。由于[0,i-1] 这个范围内有很多个递增子序列，因此，需要找到dp[j] 的最大值，然后 +1，得到dp[i]的值。

根据上述情况可以分析出有两层循环，最外层需要记录当前是哪个位置i，最里面的循环需要记录[0,i-1] 这个范围内的位置，然后每次更新dp[i]为最大值。

因此，状态转移方程为： dp[i] = Math.max(dp[i],dp[j] + 1)

3.初始化

“为了避免越界”。

对于这道题来说，在创建dp表的时候，将里面的长度全部更新为1，填表的时候，从1下标开始填，这样就可以很好的避免越界，并且可以直接表示dp[i] 长度为1这种情况。创建的dp表的规模是和原数组一样大的。

4.填表顺序

显而易见，填表顺序是：从左往右

5.返回值

由于dp表中每个位置记录的都是以当前位置为结尾的所有子序列中，最长递增子序列的长度，所以，需要遍历dp表来找到最大值，最后返回即可。

上述就是整个解决此道动态规划的分析流程，编写代码如下：
class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        if (n == 0) return 0;
        // 1.创建dp表
        // n规模大小的即可
        int[] dp = new int[n];
        // 2.初始化
        // 全部初始化为1
        Arrays.fill(dp,1);
        // 3.填表
        // 从左往右，下标为1开始填
        for (int i = 1; i < n;i++) {
            // 遍历[0,i-1]这个范围 找到最大值+1和dp[i]进行比较 
            for (int j = 0; j < i;j++) {
               // 必须要有这个前提
               if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i],dp[j] + 1);
               }
            }
        }
        // 4.返回值
        // 遍历一遍dp表，找到最大值
        int ret = 0;
        for (int i = 0; i < n;i++) {
            ret = Math.max(dp[i],ret);
        }
        return ret;
    }
}
以上就是子序列问题一道比较经典的例题解法。

小技巧 √ ：

遇到子序列的问题，分析状态转移方程的时候，一般是分为长度为1（自己）和长度大于1（0~i-1和i组合的多种情况的最大值）两种情况

5.回文串问题

例题：LCR 020. 回文子串 - 力扣（LeetCode）647. 回文子串 - 力扣（LeetCode）LCR 020. 回文子串 - 力扣（LeetCode）

1.状态表示

根据题目分析：首先要明确什么是回文字符串。使用动态规划来解决回文子串问题，需要保证能将所有的子串是否是回文的信息保存在dp表中，可以通过两层for循环来表示某个字符串的所有子串，i 位置表示起始位置，j 表示结尾位置，i ~ j 这个区间就是子字符串，因此，可以看出，再创建dp表的时候就可以创建一个二维的dp表。假设如下图是创建出的dp表：

让 i 表示起点，j 表示结尾，[0,0] 表示以0下标开始，以0下标结尾，[0,1] 表示以0开始，以1结尾，[0,2] 表示以0开始，以2结尾。[1,0] 表示以1开始，以0结尾，这种情况其实已经记录过了，就是[0,1] 这种情况，因此，dp表的主对角线下方数据都不用填，只需要填主对角线及其上方的。

dp 表中记录的是子串是否是回文的信息，因此就可以推导出状态表示(dp[i,j]) : s 字符串[i,j] 的子串，是否是回文串。

2.状态转移方程

状态转移方程就是找dp[i,j] 等于什么，对于这道题而言，[i,j] 表示的是这个区间的子字符串是不是回文字符串，因此dp表是一个boolean类型的二维数组，想要知道一个区间的字符串是不是回文字符串，首先判断i 和 j 位置的字符是不是相等，根据是否相等划分出两种情况：

当s[i] !=s[j] 时，dp[i,j] = false，当s[i] == s[j] 时，又根据i 和 j 的位置划分出三种不同的情况，当 i == j (指向同一个字符)或者 i+1 = j 时，dp[i,j] = true, 最后一种情况是:[i,j] 这个区间有很多个字符，此时就需要根据[i+1,j-1] 这个区间的boolean值来判断[i,j] 这个区间是不是回文串。

以上就是状态转移方程的分析过程。

3.初始化

避免填表的时候越界，根据状态转移方程来进行初始化，在状态转移方程中出现了 i+1 和 j-1可能越界，在第一步的时候已经说过，dp表中用到的数据都是主对角线及其上面的部分，因此i <= j，但是当 i == j 这种特殊情况已经特殊处理了，因此就不用初始化。

4.填表顺序

假设要填dp[2,5]，根据状态转移方程，需要保证dp[3,4] 已经填过了，所以填表顺序是从下往上填。

5.返回值

由于dp表中存的是所有子串是不是回文，因此，就可以找dp表中true的数量来得到回文串的数量，所以，返回值就是dp表中true的个数。

上述就是整个解决此道动态规划的分析流程，编写代码如下：
class Solution {
    public int countSubstrings(String ss) {
        int n = ss.length();
        if (n == 0) return 0;
        char[] s = ss.toCharArray();
        // 1.创建dp表
        boolean[][] dp = new boolean[n][n];
        //2.初始化
        // 无需初始化
        // 3.填表，从下往上填
        // 最外层确定起点
        for (int i = n-1; i >= 0;i--) {
            // 最里层确定重点
            for (int j = i; j < n;j++) {
                if (s[i] == s[j]) {
                    if (i == j || i+1 == j) {
                        dp[i][j] = true;
                    }else {
                        dp[i][j] = dp[i+1][j-1];
                    }
                } 
            }
        }
        // 4.返回值
        int ret = 0;
        for (int i = 0;i < n;i++) {
            for (int j = 0; j < n;j++) {
                if (dp[i][j]) {
                    ret++;
                }
            }
        }
        return ret;
    }
}
以上就是回文串问题一道比较经典的例题解法。

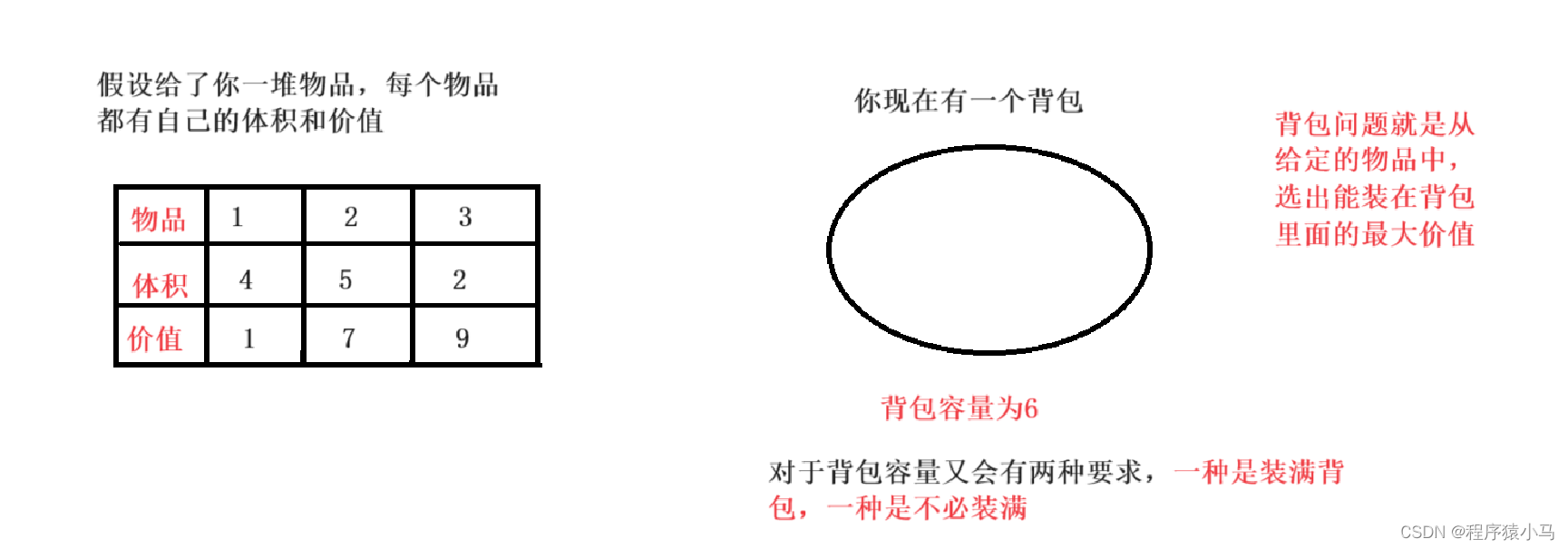
接下来两道例题都是背包问题比较经典的动态规划问题，在介绍之前补充一下什么是背包问题：

背包问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

根据给定物品的个数，可以分为如下几类：

01背包问题：每个物品只有一个

完全背包问题：每个物品有无限多个

........

背包问题如下图：

6.01背包问题

对于01背包来说，每个物品的数量都是固定的，只有一个。

例题：【模板】01背包_牛客题霸_牛客网 (nowcoder.com)

先分析题目：第一问实际上就是在问不必装满背包时，可以获得的最大价值。先来解决第一问，背包不必装满的情况。依旧是使用解决动态规划问题的五步：

1.状态表示

根据经验+题目要求来分析：题目要求最终要返回最大价值，因此dp表中需要存已挑选出的物品的最大价值，由此可以得出：dp[i] 表示从前 i 个物品中选，所有选法中，能挑选出来的最大价值。先来思考一下，这个状态转移方程是否正确？显而易见，不正确，因为这个dp表无法保证背包的容量是多少，不知道什么时候装满或者超过容量，因此，dp表还需要记录当前背包的容量，所以，将这个dp表创建成一个二维数组，横坐标表示物品的编号，纵坐标表示背包的容量。因此：dp[i][j] 表示：从前 i 个物品中挑选，总体积不超过 j，所有选法中，能挑选出来的最大价值。

2.状态转移方程

找dp[i][j] 等于什么。

对于每个位置的物品来说，都有自己的体积和价值，并且该物品有两种选择，选或者不选，因此，如果不选择 i 位置的物品，那么dp[i][j] 的最大价值就是前 i -1个物品所有选法，体积不超过 j 的最大价值，也就是 dp[i][j] = dp[i-1][j]; 如果选择 i 位置的物品,w[i] 表示 i 物品的价值，v[i] 表示 i 物品的体积，dp[i][j] = w[i] + dp[i-1][j-v[i]] (w[i] 是i物品的价值，选择 i 物品的话，就加上 i 的价值，dp[i-1][j-v[i]] 表示前 i -1 个物品中挑选，总体积不超过 j - v[i]，所有选法中的最大价值，因为 i 物品要选择，所以要保证从前往后选择物品时，有空间装下v[i],因此，从前 i-1 个物品中挑选时，体积不超过 j-v[i] 这样就保证一定能装下v[i],但是需要注意，j - v[i] >=0,必须确保能够装下i物品 )。

综上,选择两种选法中的最大值，dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-v[i]] + w[i])

3.初始化

根据状态转移方程来初始化，避免填表越界。

物品编号是从 1 开始，创建dp表时多开一行和一列，假设给的物品种类是3，背包容量是4，那么创建出的dp表就是dp[4][5]:

第一行表示：从前0个物品中挑选，体积不超过j，不选物品，那么最大价值就是0，因此第一行都是0。

第一列表示：从前i个物品中挑选，体积不超过0，每个物品都是有体积的，所有没有选法，因此第一列都是0。

状态转移方程出现了i -1，但是第一行和第一列都是0，不必初始化，从第二行开始填，就可以避免越界。由于物品下标是从1开始的，对应到物品的价值数组w 和物品的体积数组v时，需要注意下标映射。

4.填表顺序

填dp[i][j] 时，依赖前一个位置dp[i-1][j] 以及左上方位置dp[i-1][j-v[i]]，因此，填表顺序是：

从上往下。

5.返回值

在第一问中，题目要求返回的是：n个物品，总体积不超过v，所有选法中的最大价值，返回dp[n][v]即可。

以上就是01背包的第一问解题思路。

接下来解决第二问，第二问题目要求刚好装满背包，此时的最大价值

1.状态表示

状态表示分析过程和第一问的相似，直接得出结论：

dp[i][j]表示：从前 i 个物品中挑选，体积刚好等于 j，所有选法中，能挑选出来的最大价值。

2.状态转移方程

状态转移方程与第一问的一样，但是有几个小细节。

首先，如果不选择 i 物品的话，此时dp[i][j] = dp[i-1][j], 但是，可能不选择i物品且刚好从i-1个物品中挑选出体积 j 这种情况不存在，因此，将dp表中的一些值设置成 -1 ,表示当前这种情况不存在。不选择 i 物品的话，需要保证 dp[i-1][j] != -1,但是，可以直接让dp[i][j] = dp[i-1][j],即使此时这种情况不存在，也无所谓，因为dp[i][j] 也不存在。

其次，如果选择 i 物品的话，此时就要再加一个条件,和之前一样先要保证有足够背包空间装当前 i 物品的体积，也就是 j -v[i] >= 0,另一个条件就是：必须保证从前 i - 1 个物品中挑选的时候，dp[i-1][j-v[i]] 这种情况存在，也就是 dp[i-1][j-v[i]] != -1。

然后从上述两种情况取最大值：dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-v[i]] + w[i])

3.初始化

此时的初始化，由于dp表中要存 -1这种情况，因此，重新分析：

还是多开一行和一列来避免越界，此时要考虑多开的这一行和这一列的初始值。

对于第一行来说，当 i 为0时，想要前0个物品中挑选出体积为j，这种情况显然不可能，因此第一行除了dp[0][0] 其余的值均为 -1。

对于第一列来说，当 j 为0时，想要前 i 个物品中挑选出体积为0，这种情况不选即可，dp[i][0] 均为0.

如下图:

4.填表顺序

和第一问一样：从左到右

5.返回值

和第一问一样，最终返回结果应该是dp[n][v],但是需要注意，对于背包恰好装满这种情况，可能不存在，所以需要判断最终结果是不是等于 -1,然后再进行返回。

以上就是所有分析流程，详细代码如下：
import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int n = in.nextInt(); // 物品数量
            int V = in.nextInt(); // 背包体积
            int[] v = new int[n]; // 物品体积数组
            int[] w = new int[n]; // 物品价值数组
            for (int i = 0; i < n; i++) {
                v[i] = in.nextInt();
                w[i] = in.nextInt();
            }
            // 第一问结果
            int ret1 = func1(n, V, v, w);
            // 第二问结果
            int ret2 = func2(n, V, v, w);
            System.out.println(ret1);
            System.out.println(ret2);

        }
    }
    // 第一问
    public static int func1(int n, int V, int[] v, int[] w) {
        // 1.创建dp表
        int[][] dp = new int[n + 1][V + 1];
        // 2.初始化
        // 无需初始化
        // 3.填表
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= V; j++) {
                // 不选当前物品
                dp[i][j] = dp[i - 1][j];
                // 如果体积可以装当前物品，那么选当前物品 然后求最大值
                // 注意下标映射
                if (j - v[i - 1] >= 0) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i - 1]] + w[i - 1]);
                }
            }
        }
        // 4.返回值
        return dp[n][V];
    }
    // 第二问
    public static int func2(int n, int V, int[] v, int[] w) {
        // 1.创建dp表
        int[][] dp = new int[n + 1][V + 1];
        // 2.初始化
        // 第一行后续都为-1
        for (int j = 1; j <= V;j++) {
            dp[0][j] = -1;
        }
        // 3.填表
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= V; j++) {
                // 不选当前物品
                dp[i][j] = dp[i - 1][j];
                // 如果体积可以装当前物品并且dp[i-1][j-v[i]]这种情况存在，那么选当前物品 然后求最大值
                // 注意下标映射
                if (j - v[i - 1] >= 0 && dp[i-1][j-v[i-1]] != -1) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i - 1]] + w[i - 1]);
                }
            }
        }
        // 4.返回值
        return dp[n][V] == -1?0:dp[n][V];
    }
}

7.完全背包

对于完全背包来说，每个物品的数量都是无穷的。

例题：【模板】完全背包_牛客题霸_牛客网 (nowcoder.com)

该题目与01背包问题几乎相同，只是物品数量不同，因此，对题目的分析和上述基本类似，此处不过多赘述，先来求解第一问。

1.状态表示

和01背包的状态表示相同：

dp[i][j] 表示：从前 i 个物品中挑选，总体积不超过 j，所有选法中，能挑选出来的最大价值。

2.状态转移方程

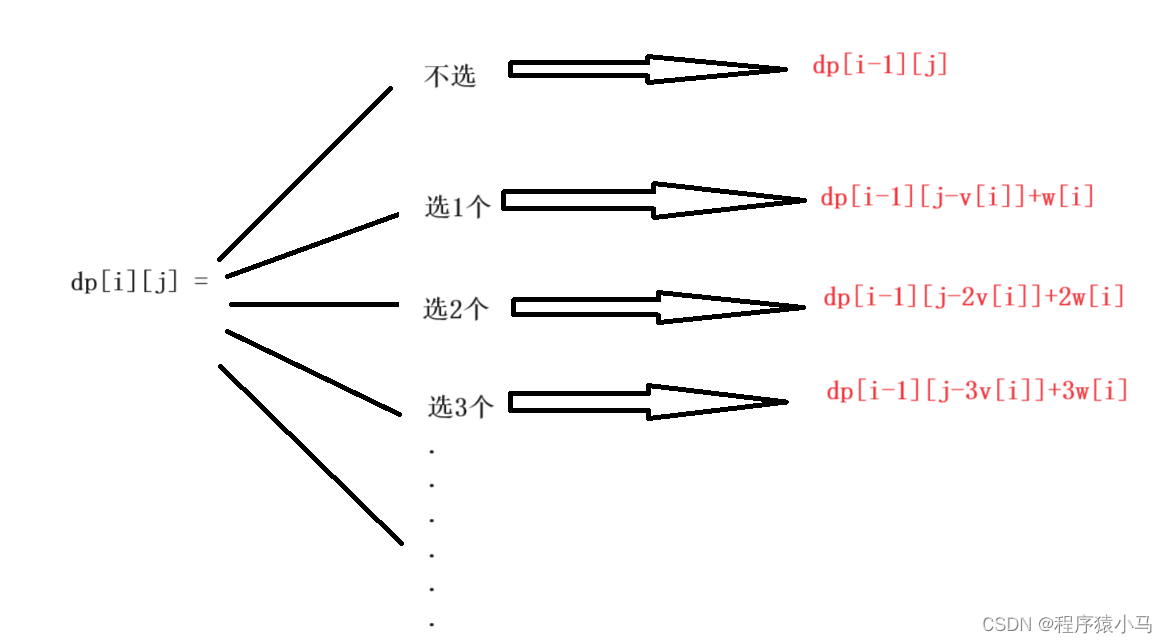
对于01背包来说，由于物品只有一个，因此每个物品只有选和不选两种情况，但是完全对于完全背包而言，由于物品个数有无穷个，因此，每个物品有很多种选择，包括不选、选一个、选两个、选三个...... 对于不选当前物品来说，其状态转移方程dp[i][j] = dp[i-1][j]，对于选1个物品来说，其状态转移方程dp[i][j] = dp[i-1][j-v[i]] + w[i],也就是01背包的另一个状态转移方程，对于选2个物品来说，其状态转移方程dp[i][j] = dp[i-1][j-2v[i]] + 2w[i](也就是当前 i 物品选两次，其价值就是2w[i],然后从前面i-1个物品中挑选，体积不超过j-2v[i]),对于选3个物品来说，其状态转移方程dp[i][j] = dp[i-1][j-3v[i]] + 3w[i]......

对于dp[i][j] 而言，是从上面的所有情况中找最大值，因此：

上图就是状态转移方程的推导过程。

3.初始化

根据状态转移方程来初始化，避免填表越界。

物品编号是从 1 开始，创建dp表时多开一行和一列，假设给的物品种类是3，背包容量是4，那么创建出的dp表就是dp[4][5]:

第一行表示：从前0个物品中挑选，体积不超过j，不选物品，那么最大价值就是0，因此第一行都是0。

第一列表示：从前i个物品中挑选，体积不超过0，每个物品都是有体积的，所有没有选法，因此第一列都是0。

状态转移方程出现了i -1，但是第一行和第一列都是0，不必初始化，从第二行开始填，就可以避免越界。由于物品下标是从1开始的，对应到物品的价值数组w 和物品的体积数组v时，需要注意下标映射。

对于dp[i-1][j-v[i]]+w[i],这种情况来说，可能会存在j-v[i] 不存在，也就是 j-v[i] < 0,因此，在使用的时候需要注意判断。

4.填表顺序

想要填dp[i][j] 位置，依赖dp[i-1][j],说明从上往下填，又依赖dp[i][j-v[i]] + w[i],说明只能从左往右填，综上，填表顺序：从上往下并且从左到右

5.返回值

第一问题目要求背包最多能装下的最大价值，因此，返回dp[n][v]

以上就是01背包的第一问解题思路。

接下来解决第二问，第二问题目要求刚好装满背包，此时的最大价值

1.状态表示

状态表示分析过程和第一问的相似，直接得出结论：

dp[i][j]表示：从前 i 个物品中挑选，体积刚好等于 j，所有选法中，能挑选出来的最大价值

2.状态转移方程

状态转移方程与第一问的一样：dp[i][j] = max(dp[i-1][j],dp[i][j-v[i]]+w[i])

但是有几个小细节。

首先，如果不选择 i 物品的话，此时dp[i][j] = dp[i-1][j], 但是，可能不选择i物品且刚好从i-1个物品中挑选出体积 j 这种情况不存在，因此，将dp表中的一些值设置成 -1 ,表示当前这种情况不存在。不选择 i 物品的话，需要保证 dp[i-1][j] != -1,但是，可以直接让dp[i][j] = dp[i-1][j],即使此时这种情况不存在，也无所谓，因为dp[i][j] 也不存在。

其次，如果选择 i 物品(1个、2个、3个......)的话，此时就要再加一个条件,和之前一样先要保证有足够背包空间装当前 i 物品的体积，也就是 j -v[i] >= 0,另一个条件就是：必须保证

dp[i][j-v[i]] 这种情况存在，也就是 dp[i][j-v[i]] != -1。

3.初始化

此时的初始化，由于dp表中要存 -1这种情况，因此，重新分析：

还是多开一行和一列来避免越界，此时要考虑多开的这一行和这一列的初始值。

对于第一行来说，当 i 为0时，想要前0个物品中挑选出体积为j，这种情况显然不可能，因此第一行除了dp[0][0] 其余的值均为 -1。

对于第一列来说，当 j 为0时，想要前 i 个物品中挑选出体积为0，这种情况不选即可，dp[i][0] 均为0.

如下图:

4.填表顺序

和第一问相同，从上到下并且从左到右

5.返回值

在返回之前，需要判断dp[n][v] 这种情况是否存在，因为对于背包恰好装满这种情况可能不存在。

以上就是所有分析流程，详细代码如下：
import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int n = in.nextInt();// 物品个数
            int bagV = in.nextInt();// 背包体积
            int[] v = new int[n];// 物品体积
            int[] w = new int[n];// 物品价值
            for (int i = 0; i < n; i++) {
                v[i] = in.nextInt();
                w[i] = in.nextInt();
            }
            // 第一问
            int ret1 = func1(n, bagV, v, w);
            System.out.println(ret1);
            // 第二问
            int ret2 = func2(n, bagV, v, w);
            System.out.println(ret2);
        }
    }
    // 第一问
    public static int func1(int n, int bagV, int[] v, int[] w) {
        // 1.创建dp表
        //多开一行一列
        int[][] dp = new int[n + 1][bagV + 1];
        // 2.初始化
        // 不用初始化
        // 3.填表
        // 从上往下并且从左到右
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= bagV; j++) {
                // 不选该物品
                dp[i][j] = dp[i - 1][j];
                // 和另外的状态转移方程对于求最大值
                // 注意下标映射
                if (j - v[i - 1] >= 0) {
                    dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);
                }
            }
        }
        // 4.返回值
        return dp[n][bagV];
    }
    // 第二问
    public static int func2(int n, int bagV, int[] v, int[] w) {
        // 1.创建dp表
        //多开一行一列
        int[][] dp = new int[n + 1][bagV + 1];
        // 2.初始化
        for (int j = 1;j <= bagV;j++) {
            dp[0][j] = -1;
        }
        // 3.填表
        // 从上往下并且从左到右
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= bagV; j++) {
                // 不选该物品
                dp[i][j] = dp[i - 1][j];
                // 和另外的状态转移方程对于求最大值
                // 注意下标映射
                if (j - v[i - 1] >= 0 && dp[i][j-v[i-1]] != -1) {
                    dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);
                }
            }
        }
        // 4.返回值
        // 返回之前判断是否可以装满
        return dp[n][bagV] == -1?0:dp[n][bagV];
    }
}