数据结构OJ实验9-图存储结构和遍历

news2024/11/26 21:43:01

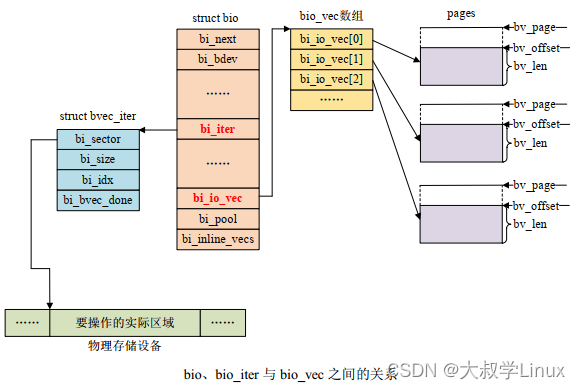
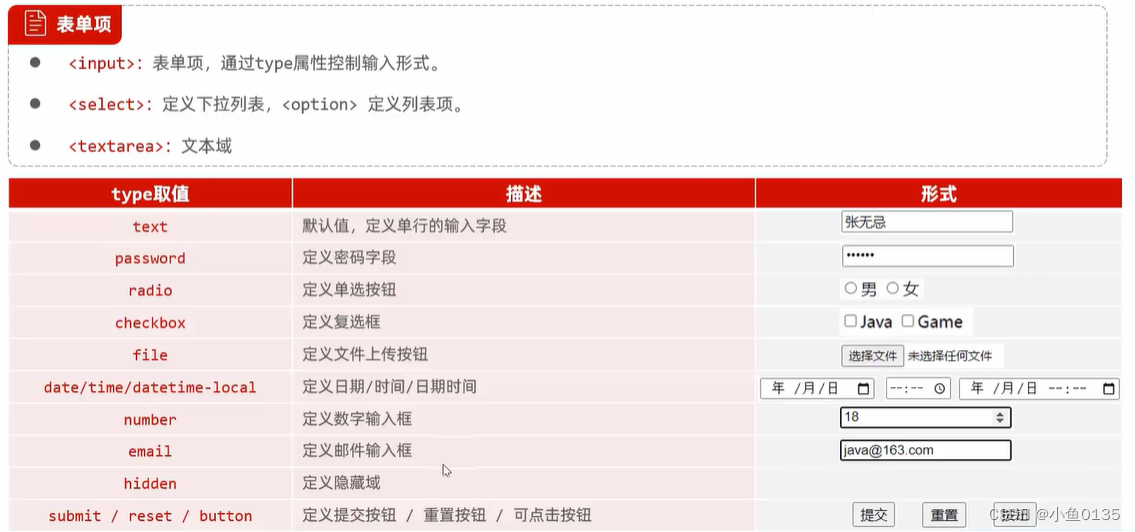
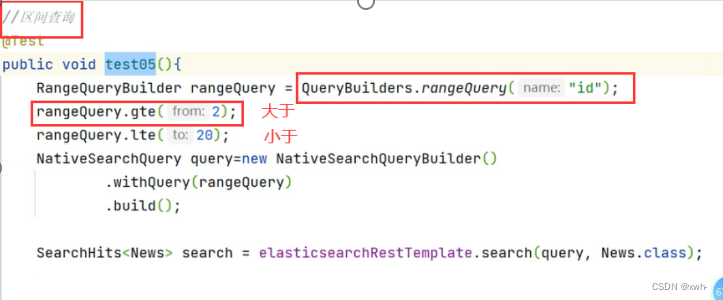
A. 图综合练习--构建邻接表

题目描述

已知一有向图，构建该图对应的邻接表。

邻接表包含数组和单链表两种数据结构，其中每个数组元素也是单链表的头结点，数组元素包含两个属性，属性一是顶点编号info，属性二是指针域next指向与它相连的顶点信息。

单链表的每个结点也包含两个属性，属性一是顶点在数组的位置下标，属性二是指针域next指向下一个结点。

输入

第1行输入整数t，表示有t个图

第2行输入n和k，表示该图有n个顶点和k条弧。

第3行输入n个顶点。

第4行起输入k条弧的起点和终点，连续输入k行

以此类推输入下一个图

输出

输出每个图的邻接表，每行输出格式：数组下标 顶点编号-连接顶点下标-......-^，数组下标从0开始。

具体格式请参考样例数据，每行最后加入“^”表示NULL。

样例查看模式 

正常显示查看格式

输入样例1 

1\n
5 7\n
A B C D E\n
A B\n
A D\n
A E\n
B D\n
C B\n
C E\n
E D\n

输出样例1

0 A-1-3-4-^\n
1 B-3-^\n
2 C-1-4-^\n
3 D-^\n
4 E-3-^\n

AC代码

#include<iostream>
#include<vector>
#include<map>
using namespace std;
class graph
{
	int n, k;
	vector<int>h;
	vector<int>ne;
	vector<int>e;
	int idx;
	map<char, int>id;
	vector<char>value;
public:
	graph()
	{
		idx = 0;
		cin >> n >> k;
		h.resize(2 * n, -1);
		ne.resize(2 * n);
		e.resize(2 * n);
		for (int i = 0; i < n; i++)
		{
			char c;
			cin >> c;
		    id[c] = i;
			value.push_back(c);
		}
		for (int i = 0; i < k; i++)
		{
			char u, v;
			cin >> u >> v;
			add(id[u], id[v]);
		}
	}
	void add(int a, int b)
	{
		e[idx] = b;
		ne[idx] = h[a];
		h[a] = idx++;
	}
	void show()
	{
		for (int i = 0; i < n; i++)
		{
			cout << i << " " << value[i] << "-";
			vector<int>ans;
			for (int j = h[i]; ~j; j = ne[j])
			{
				int k = e[j];
				ans.push_back(id[value[k]]);
			}
			//由于本题使用头插法，而此方法是尾插法，故要逆转
			for (int i=ans.size()-1;i>=0;i--)
			{
				cout << ans[i] << "-";
			}
			cout << "^" << endl;
		}
	}
};
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		graph g;
		g.show();
	}
	return 0;
}

B. DS图—图的邻接矩阵存储及度计算

题目描述

假设图用邻接矩阵存储。输入图的顶点信息和边信息，完成邻接矩阵的设置，并计算各顶点的入度、出度和度，并输出图中的孤立点（度为0的顶点）

--程序要求--

若使用C++只能include一个头文件iostream；若使用C语言只能include一个头文件stdio

程序中若include多过一个头文件，不看代码，作0分处理

不允许使用第三方对象或函数实现本题的要求

输入

测试次数T，每组测试数据格式如下：

图类型  顶点数 （D—有向图，U—无向图）

顶点信息

边数

每行一条边（顶点1 顶点2）或弧（弧尾 弧头）信息

输出

每组测试数据输出如下信息（具体输出格式见样例）：

图的邻接矩阵

按顶点信息输出各顶点的度（无向图）或各顶点的出度  入度  度（有向图）。孤立点的度信息不输出。

图的孤立点。若没有孤立点，不输出任何信息。

样例查看模式 

正常显示查看格式

输入样例1 

2\n
D 5\n
V1 V2 V3 V4 V5\n
7\n
V1 V2\n
V1 V4\n
V2 V3\n
V3 V1\n
V3 V5\n
V4 V3\n
V4 V5\n
U 5\n
A B C D E\n
5\n
A B\n
A C\n
B D\n
D C\n
A D

输出样例1

0 1 0 1 0\n
0 0 1 0 0\n
1 0 0 0 1\n
0 0 1 0 1\n
0 0 0 0 0\n
V1: 2 1 3\n
V2: 1 1 2\n
V3: 2 2 4\n
V4: 2 1 3\n
V5: 0 2 2\n
0 1 1 1 0\n
1 0 0 1 0\n
1 0 0 1 0\n
1 1 1 0 0\n
0 0 0 0 0\n
A: 3\n
B: 2\n
C: 2\n
D: 3\n
E

AC代码

#include<iostream>
using namespace std;
//输入测试次数，每组测试：
//图类型，顶点数
//顶点信息，边数，每条边的头尾
//输出每个点的出度和入度，单独输出孤立点
class Map
{
    int vertexnum;
    string* vertex;
    int** adjmatrix;
    char kind;
public:
    Map()
    {
        cin >> kind >> vertexnum;
        vertex = new string[vertexnum];
        for (int i = 0; i < vertexnum; i++)
        {
            cin >> vertex[i];
        }
        adjmatrix = new int* [vertexnum];
        for (int i = 0; i < vertexnum; i++)
        {
            adjmatrix[i] = new int[vertexnum];
            for (int j = 0; j < vertexnum; j++)
            {
                adjmatrix[i][j] = 0;
            }
        }
        int n;
        cin >> n;
        for (int i = 0; i < n; i++)
        {
            string s1, s2;
            cin >> s1 >> s2;
            int index1 = 0;
            int index2 = 0;
            for (int j = 0; j < vertexnum; j++)
            {
                if (vertex[j] == s1)
                {
                    index1 = j;
                    break;
                }
            }
            for (int j = 0; j < vertexnum; j++)
            {
                if (vertex[j] == s2)
                {
                    index2 = j;
                    break;
                }
            }
            switch (kind)
            {
            case 'U':
                adjmatrix[index2][index1] = 1;
            case 'D':
                adjmatrix[index1][index2] = 1;
            default:
                break;
            }
        }
    }
    void display_array()
    {
        for (int i = 0; i < vertexnum; i++)
        {
            cout << adjmatrix[i][0];
            for (int j = 1; j < vertexnum; j++)
            {
                cout << " " << adjmatrix[i][j];
            }
            cout << endl;
        }
    }
    void display_node()
    {
        if (kind == 'U')
        {
            for (int i = 0; i < vertexnum; i++)
            {
                int cnt = 0;
                for (int j = 0; j < vertexnum; j++)
                {
                    if (adjmatrix[i][j] != 0)
                    {
                        cnt++;
                    }
                }
                if (cnt)
                {
                    cout << vertex[i] << ": " << cnt << endl;
                }
                else
                {
                    cout << vertex[i] << endl;
                }
            }
        }
        else if (kind == 'D')
        {
            for (int i = 0; i < vertexnum; i++)
            {
                int cnt1 = 0;
                for (int j = 0; j < vertexnum; j++)
                {
                    if (adjmatrix[i][j] != 0)
                    {
                        cnt1++;
                    }
                }
                int cnt2 = 0;
                for (int j = 0; j < vertexnum; j++)
                {
                    if (adjmatrix[j][i] != 0)
                    {
                        cnt2++;
                    }
                }
                if (cnt1 || cnt2)//存在其中一个就不是孤立点
                {
                    cout << vertex[i] << ": " << cnt1 << " " << cnt2 << " " << cnt1 + cnt2 << endl;
                }
                else
                {
                    cout << vertex[i] << endl;
                }
            }
        }
    }
    ~Map()
    {
        delete[]vertex;
        for (int i = 0; i < vertexnum; i++)
        {
            delete[]adjmatrix[i];
        }
        delete[]adjmatrix;
    }
};
int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        Map m;
        m.display_array();
        m.display_node();
    }
    return 0;
}

C. DS图遍历--深度优先搜索

题目描述

给出一个图的邻接矩阵，对图进行深度优先搜索，从顶点0开始

代码框架参考课本P169算法7.4和7.5，同学们可在理解的基础上自行设计算法，不强制要求完全相同

注意：图n个顶点编号从0到n-1

输入

第一行输入t，表示有t个测试实例

第二行输入n，表示第1个图有n个结点

第三行起，每行输入邻接矩阵的一行，以此类推输入n行

第i个结点与其他结点如果相连则为1，无连接则为0，数据之间用空格隔开

以此类推输入下一个示例

输出

每行输出一个图的深度优先搜索结果，结点编号之间用空格隔开

样例查看模式 

正常显示查看格式

输入样例1 

2\n
4\n
0 0 1 1\n
0 0 1 1\n
1 1 0 1\n
1 1 1 0\n
5\n
0 0 0 1 1\n
0 0 1 0 0\n
0 1 0 1 1\n
1 0 1 0 0\n
1 0 1 0 0\n

输出样例1

0 2 1 3 \n
0 3 2 1 4 \n

AC代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        vector<vector<int>>v(n);
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                int x;
                cin >> x;
                v[i].push_back(x);
            }
        }
        vector<int>st(n);//标记是否已经走过
        stack<int>s;//深度优先搜索使用栈
        for (int i = 0; i < n; i++)//每个结点都要搜一次，确定每个都走过
        {
            if (st[i])continue;
            s.push(i);
            while (!s.empty())//每个点开始搜
            {
                auto t = s.top();
                s.pop();
                if (st[t])continue;
                st[t] = 1;
                cout << t << " ";//满足条件可以搜
                //注意逆序枚举连接点
                //因为是栈，先进去后出来
                for (int j = n - 1; j >= 0; j--)
                {
                    if (v[t][j] && !st[j])
                    {
                        s.push(j);
                    }
                }
            }
        }
        cout << endl;
    }
    return 0;
}

D. DS图遍历--广度优先搜索

题目描述

给出一个图的邻接矩阵，对图进行广度优先搜索，从顶点0开始

注意：图n个顶点编号从0到n-1

输入

第一行输入t，表示有t个测试实例

第二行输入n，表示第1个图有n个结点

第三行起，每行输入邻接矩阵的一行，以此类推输入n行

第i个结点与其他结点如果相连则为1，无连接则为0，数据之间用空格隔开

以此类推输入下一个示例

输出

每行输出一个图的广度优先搜索结果，结点编号之间用空格隔开

样例查看模式 

正常显示查看格式

输入样例1 

2\n
4\n
0 0 1 1\n
0 0 1 1\n
1 1 0 1\n
1 1 1 0\n
5\n
0 0 0 1 1\n
0 0 1 0 0\n
0 1 0 1 1\n
1 0 1 0 0\n
1 0 1 0 0\n

输出样例1

0 2 3 1 \n
0 3 4 2 1 \n

AC代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        vector<vector<int>>v(n);
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                int x;
                cin >> x;
                v[i].push_back(x);
            }
        }
        vector<int>st(n);//标记是否已经走过
        queue<int>s;//广度搜索使用队列
        for (int i = 0; i < n; i++)//每个结点都要搜一次，确定每个都走过
        {
            if (st[i])continue;
            s.push(i);
            while (!s.empty())//每个点开始搜
            {
                auto t = s.front();
                s.pop();
                if (st[t])continue;
                st[t] = 1;
                cout << t << " ";//满足条件可以搜
                //注意顺序枚举连接点
                //因为是队列，先进去先出来
                for (int j = 0; j<=n-1;j++)
                {
                    if (v[t][j] && !st[j])
                    {
                        s.push(j);
                    }
                }
            }
        }
        cout << endl;
    }
    return 0;
}

E. DS图—图非0面积

题目描述

编程计算由"1"围成的下列图形的面积。面积计算方法是统计"1"所围成的闭合曲线中"0"点的数目。如图所示，在10*10的二维数组中，"1"围住了15个点，因此面积为15。

提示：queue

输入

测试次数t

每组测试数据格式为：

数组大小m,n

一个由0和1组成的m*n的二维数组

输出

对每个二维数组，输出符号"1"围住的"0"的个数，即围成的面积。假设一定有1组成的闭合曲线，但不唯一。

样例查看模式 

正常显示查看格式

输入样例1 

2\n
10 10\n
0 0 0 0 0 0 0 0 0 0\n
0 0 0 0 1 1 1 0 0 0\n
0 0 0 0 1 0 0 1 0 0\n
0 0 0 0 0 1 0 0 1 0\n
0 0 1 0 0 0 1 0 1 0\n
0 1 0 1 0 1 0 0 1 0\n
0 1 0 0 1 1 0 1 1 0\n
0 0 1 0 0 0 0 1 0 0\n
0 0 0 1 1 1 1 1 0 0\n
0 0 0 0 0 0 0 0 0 0\n
5 8\n
0 1 1 0 0 1 1 0\n
1 0 1 0 1 0 0 1\n
0 1 0 1 0 0 1 0\n
0 1 0 0 1 1 1 0\n
0 0 0 0 0 0 0 0\n

输出样例1

15\n
5\n

#include<bits/stdc++.h>
using namespace std;
int n,m;
int dx[]={1,-1,0,0};
int dy[]={0,0,-1,1};
vector<vector<int>>v;
void dfsfind(int x,int y)
{
    if(x<0||y<0||x>=m||y>=n||v[x][y])
    return;
    v[x][y]=1;
    for(int i=0;i<4;i++)
    {
        dfsfind(x+dx[i],y+dy[i]);
    }
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        v.clear();
        cin>>m>>n;
        v.resize(m);
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int x;
                cin>>x;
                v[i].push_back(x);
            }
        }
        int ans=0;
        for(int i=0;i<m;i++)//先按行
        {
            dfsfind(i,0);
            dfsfind(i,n-1);
        }
        for(int i=0;i<n;i++)//后按列
        {
            dfsfind(0,i);
            dfsfind(m-1,i);
        }
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(v[i][j]==0)ans++;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

F. 社交网络图中结点的“重要性”计算

题目描述

在社交网络中，个人或单位（结点）之间通过某些关系（边）联系起来。他们受到这些关系的影响，这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用，可以增强也可以减弱。而结点根据其所处的位置不同，其在网络中体现的重要性也不尽相同。

“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标，即一个有较高中心性的结点比有较低中心性的结点能够更快地（平均意义下）到达网络中的其它结点，因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中，结点vi​的“紧密度中心性”Cc(vi​)数学上定义为vi​到其余所有结点vj​ (j=i) 的最短距离d(vi​,vj​)的平均值的倒数：

对于非连通图，所有结点的紧密度中心性都是0。

给定一个无权的无向图以及其中的一组结点，计算这组结点中每个结点的紧密度中心性。

输入

输入第一行给出两个正整数N和M，其中N（≤104）是图中结点个数，顺便假设结点从1到N编号；M（≤105）是边的条数。随后的M行中，每行给出一条边的信息，即该边连接的两个结点编号，中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K（≤100）以及K个结点编号，用空格分隔。

输出

按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性，每个输出占一行，结果保留到小数点后2位。

样例查看模式 

正常显示查看格式

输入样例1 

9 14\n
1 2\n
1 3\n
1 4\n
2 3\n
3 4\n
4 5\n
4 6\n
5 6\n
5 7\n
5 8\n
6 7\n
6 8\n
7 8\n
7 9\n
3 3 4 9

输出样例1

Cc(3)=0.47\n
Cc(4)=0.62\n
Cc(9)=0.35

AC代码

#include<bits/stdc++.h>
using namespace std;
//求一个点到其余各点的最短路->FLoyd
const int N = 1000, inf = 1e9;
long long res = 0;
int n, m, k;
int d[N][N];
void floyd()
{
    for (int k = 1; k <= n; k++)//中间点枚举放在首个循环
    {
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            }
        }
    }
}
int main()
{
    cin >> n >> m;
    //注意弗洛伊德的初始
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            if (i == j)d[i][j] = 0;
            else d[i][j] = inf;
        }
    }
    for (int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        d[a][b] = d[b][a] = 1;//无向图
    }
    floyd();
    bool flag = 0;
    cin >> k;
    for (int i = 0; i < k; i++) {
        res = 0;
        int x;
        cin >> x;
        if (!flag)
        {
            for (int j = 1; j <= n; j++)
            {
                if (x == j)continue;
                if (d[x][j] > inf / 2)//此时不连通
                {
                    flag = 1;
                    break;
                }
                res += d[x][j];
            }
        }
        if (flag)printf("Cc(%d)=0.00\n", x);//无法满足到其余所有点
        else
        {
            double ans = (double)(n - 1) / res;
            printf("Cc(%d)=%.2lf\n", x, ans);
        }
    }
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1349560.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数据结构期末复习（fengkao课堂）

数据结构期末复习（fengkao课堂）

学习数据结构时&#xff0c;以下建议可能对您有所帮助&#xff1a; 理解基本概念&#xff1a;首先&#xff0c;确保您理解数据结构的基本概念&#xff0c;例如数组、链表、栈、队列、树、图等。了解它们的定义、特点和基本操作。 学习时间复杂度和空间复杂度&#xff1a;了解如…
阅读更多...
【LeetCode:34. 在排序数组中查找元素的第一个和最后一个位置 | 二分】

【LeetCode:34. 在排序数组中查找元素的第一个和最后一个位置 | 二分】

&#x1f680; 算法题 &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;…
阅读更多...
simulink代码生成（八）——应用串口输入的16进制数

simulink代码生成（八）——应用串口输入的16进制数

1、串口输入的是16进制数&#xff0c;如何将其应用到算法中&#xff1f; 串口输入的数据是16进制数&#xff1b;要解决这个问题必须要理解matlab的数据类型&#xff1b;数据类型一般用来标明数据的系列参数&#xff0c;包含有精度、动态范围、性能和存储的资源。模型会默认使…
阅读更多...
你好2024！

你好2024！

大家好&#xff0c;我是小悟 2024年1月1日&#xff0c;新年的第一天&#xff0c;阳光明媚&#xff0c;空气中弥漫着希望和新的开始的气息。在这个特别的日子里&#xff0c;大家纷纷走出家门&#xff0c;迎接新年的到来。 街道上&#xff0c;熙熙攘攘的人群中&#xff0c;有孩…
阅读更多...
开放原子训练营（第四季）TobudOS——TobudOS内核移植（keil版）

开放原子训练营（第四季）TobudOS——TobudOS内核移植（keil版）

前言 12月份参加了开放原第四季线下活动&#xff0c;觉得很有意义。通过这篇博文&#xff0c;记录一下这次活动进行的移植TobudOS内核的过程&#xff0c;下面就让我们开始吧。 开发板介绍 本次使用的开发板型号为STM32H750&#xff0c;当然了&#xff0c;其他型号的开发版也…
阅读更多...
Django 实现Web便签

Django 实现Web便签

效果图 会用到的知识 目录结构与URL路由注册request与response对象模板基础与模板继承ORM查询后台管理 实现步骤 1. terminal 输入 django-admin startapp the_10回车 2. 注册&#xff0c; 在 tutorial子文件夹settings.py INSTALLED_APPS 中括号添加 "the_10" IN…
阅读更多...
C++日期类的实现

C++日期类的实现

前言&#xff1a;在类和对象比较熟悉的情况下&#xff0c;我们我们就可以开始制作日期表了&#xff0c;实现日期类所包含的知识点有构造函数&#xff0c;析构函数&#xff0c;函数重载&#xff0c;拷贝构造函数&#xff0c;运算符重载&#xff0c;const成员函数 1.日期类的加减…
阅读更多...
pyqt5用qtdesign设计页面时，去掉页面的空白界面、边框和标题栏

pyqt5用qtdesign设计页面时，去掉页面的空白界面、边框和标题栏

前言 Windows默认的标题栏有时候自己觉得不太美观&#xff0c;就想自己设计一个&#xff0c;然后把默认的去掉&#xff0c;并且把长方形的边框和多余的空表界面去掉&#xff0c;就是下图中圈出来的区域&#xff1a; 去掉之后的效果如图&#xff1a; 这样我们就可以自定义窗…
阅读更多...
SpringBoot + Vue 抖音全平台项目

SpringBoot + Vue 抖音全平台项目

简介 本项目是一个短视频平台&#xff0c;拥有热度排行榜&#xff0c;热门视频&#xff0c;兴趣推送&#xff0c;关注推送&#xff0c;内容审核等功能。 源码下载 网盘 (访问密码: 8418) 登录/注册 首页 创作中心 架构设计 上传视频业务流程 视频推送流程 1.用户订阅分类后…
阅读更多...
OSPFv2 LSA类型

OSPFv2 LSA类型

OSPFv2需要了解的6种LSA&#xff0c;分别是&#xff1a;1类LSA、2类LSA、3类LSA、4类LSA、5类LSA、7类LSA。 我们先了解一下LSA的组成&#xff0c;LSA由LSA头部和LSA内容组成&#xff0c;其中LSA头部是每一类LSA都相同的&#xff0c;有Type&#xff08;LSA的类型&#xff09;、…
阅读更多...
iMazing 2 .17.16最新官方中文版免费下载安装激活

iMazing 2 .17.16最新官方中文版免费下载安装激活

iMazing 2 .17.16最新版是一款帮助用户管理IOS手机的应用程序&#xff0c;iMazing2最新版能力远超iTunes提供的终极的iOS设备管理器。IMazing与你的iOS设备(iPhone、 iPad或iPod)相连&#xff0c;使用起来非常的方便。作为苹果指定的iOS设备同步工具。 mazing什么意思 iMazing…
阅读更多...
软件推荐：MobaXterm

软件推荐：MobaXterm

介绍 MobaXterm 是远程计算的终极工具箱&#xff0c;它提供了几乎所有重要的远程网络工具&#xff0c;SSH、RDP、FTP、VNC&#xff0c;只要你能想到的&#xff0c;都可以在MobaXterm中找到。除了海量协议外&#xff0c;MobaXterm 还支持安装额外的插件来扩展其功能。 软件官网…
阅读更多...
深度学习核心技术与实践之自然语言处理篇

深度学习核心技术与实践之自然语言处理篇

非书中全部内容&#xff0c;只是写了些自认为有收获的部分。 自然语言处理简介 NLP的难点 &#xff08;1&#xff09;语言有很多复杂的情况&#xff0c;比如歧义、省略、指代、重复、更正、倒序、反语等 &#xff08;2&#xff09;歧义至少有如下几种&#xff1a; …
阅读更多...
Linux学习第49天：Linux块设备驱动实验（一）：Linux三大驱动之一

Linux学习第49天：Linux块设备驱动实验（一）：Linux三大驱动之一

Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 本章学习Linux三大驱动之一的块设备驱动&#xff0c;主要应用场景为存储设备。 本章的思维导图如下&#xff1a; 一、什么是块设备 块设备---存储设备 以块为单位…
阅读更多...
经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现

经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现

经典目标检测YOLO系列(一)复现YOLOV1(3)正样本的匹配及损失函数的实现 之前&#xff0c;我们依据《YOLO目标检测》(ISBN:9787115627094)一书&#xff0c;提出了新的YOLOV1架构&#xff0c;并解决前向推理过程中的两个问题&#xff0c;继续按照此书进行YOLOV1的复现。 经典目标…
阅读更多...
数据结构OJ实验8-赫夫曼树编码及应用

数据结构OJ实验8-赫夫曼树编码及应用

A. DS二叉树--赫夫曼树的构建与编码 题目描述 给定n个权值&#xff0c;根据这些权值构造huffman树&#xff0c;并进行huffman编码 大家参考课本算法6.12为主&#xff0c;注意数组访问是从位置1开始 要求&#xff1a;赫夫曼的构建中&#xff0c;默认左孩子权值不大于右孩子权…
阅读更多...
webRTC实时通信demo

webRTC实时通信demo

参考文档&#xff1a; https://www.jianshu.com/p/f439ce5cc0be https://www.w3cschool.cn/socket demo流程示意图&#xff08;用户A向用户B推送视频&#xff09;&#xff1a; #mermaid-svg-0KZaDQ5DBl28zjmZ {font-family:"trebuchet ms",verdana,arial,sans-seri…
阅读更多...
JavaWeb——前端之HTMLCSS

JavaWeb——前端之HTMLCSS

学习视频链接&#xff1a;https://www.bilibili.com/video/BV1m84y1w7Tb/?spm_id_from333.999.0.0 一、Web开发 1. 概述 能通过浏览器访问的网站 2. Web网站的开发模式——主流是前后端分离 二、前端Web开发 1. 初识 前端编写的代码通过浏览器进行解析和渲染得到我们看到…
阅读更多...
elasticsearch+Kibana

elasticsearch+Kibana

什么是es(elasticsearch) Elasticsearch是一个开源的分布式搜索和分析引擎&#xff0c;它构建在Apache Lucene搜索引擎库之上。它提供了一个分布式多用户能力的实时搜索和分析引擎&#xff0c;能够处理大规模的数据。Elasticsearch被广泛用于构建全文搜索、日志分析、实时应用…
阅读更多...
灸哥问答：软件架构在软件研发中的作用

灸哥问答：软件架构在软件研发中的作用

软件架构在软件开发中扮演着至关重要的角色。我们在软件研发的过程中&#xff0c;类比于建造一座公寓楼&#xff0c;而软件架构就像是盖楼之前的设计图纸&#xff0c;如果没有设计图纸就直接盖楼&#xff0c;可想而知带来的后果是什么。我对软件架构的作用表现总结如下&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023