大家好我是苏麟, 今天继续聊图 .
与前面的链表、树等相比,图的存储和遍历要复杂非常多 .所以理解就好 , 面试基本不会让写代码的 .
图的类型多、表示方式多,相关算法也很多,实现又过于复杂,多语言实现难度太大了。这些算法一般理解就好,不需要面试的时候手写 .
图的实现方式
图的表示方式比前面学习的几种结构都复杂,常见的有两种 : 二维数组表示(邻接矩阵),链表表示(邻接表)。
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于 n 个顶点的图而言,矩阵是的 row 和 col 表示的是 1....n个点,矩阵中的1表示有连线,0表示没有连线。

在上图的邻接矩阵需要为每个顶点都分配n个边的空间,其实有很多边都是不存在,因此存储效率比较低。如果图比较稀疏的话,会造成大量的空间浪费,比如在地铁图中,一个站点多的也就与几个站相连少的只有一个,而使用邻接矩阵则需要为每个站点都分配N个空间。
邻接表的实现只关心存在的边,不关心不存在的边,因此没有空间浪费,邻接表由数组+链表组成。

图的遍历
与树一样,图有深度优先和层次遍历两种方式,但是图没有根,因此更多时候将层次遍历称为广度优先遍历BFS。
图的深度优先搜索
深度优先搜索(Depth First Search) 简称深搜或者 DFS,是遍历图存储结构的一种算法,既适用于无向图 (网),也适用于有向图 (网)。
所谓图的遍历,简单理解就是逐个访问图中的顶点,确保每个顶点都只访问一次.
首先通过一个样例,给大家讲解深度优先搜索算法是如何实现图的遍历的 .
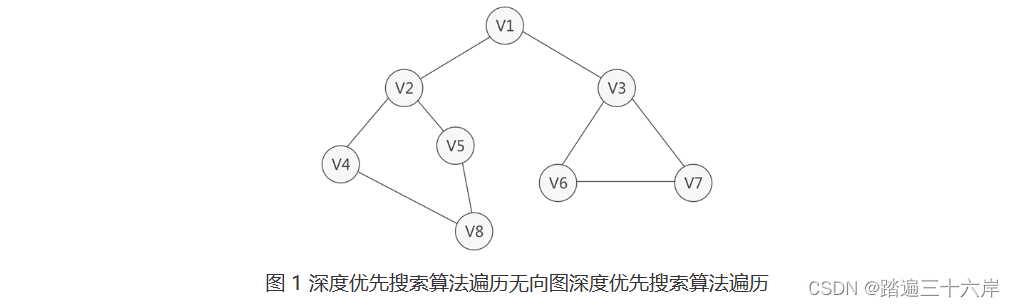
图 1无向图的整个过程是 :
1.初始状态下,无向图中的所有顶点都是没有被访问过的,因此可以任选一个顶点出发,遍历整个无向图。
假设从 V1 顶点开始,先访问 V1 顶点,如下图所示 :

2. 紧邻 V1 的顶点有两个,分别是 V2 和 V3,它们都没有被访问过,从它们中任选一个,比如访问 V2 ,. 如下图所示 :

3. 紧邻 V2 的顶点有三个,分别是 V1、V4和 V5,尚未被访问的有 V4 和 V5,从它们中任选一个,比如访问 V4,如下图所示:

4 . 紧邻 V4 的顶点有两个,分别是 V2 和 V8,只有 V8 尚未被访问,因此访问 V8,如下图所示 :

5 . 紧邻 V8 的顶点有两个,分别是 V4 和 V5,只有 V5 尚未被访问,因此访问 V5,如下图所示:

6 . 和 V5 相邻的顶点有两个,分别是 V2 和 V8,它们都已经访问过了。也就是说,此时从 V5 出发,找不到任何未被访问的顶点了。
这种情况下,深度优先搜索算法会回退到之前的顶点,查看先前有没有漏掉的、尚未访问的顶点:
- 从 V5 回退到 V8,找不到尚未访问的顶点
- 从 V8 回退到 V4,还是找不到尚未访问的顶点
- 从 V4 回退到 V2,也还是找不到尚未访问的顶点
- 从 V2 回退到 V1,发现 V3 还没有被访问。于是,下一个要访问的顶点就是 V3,如下图所示:
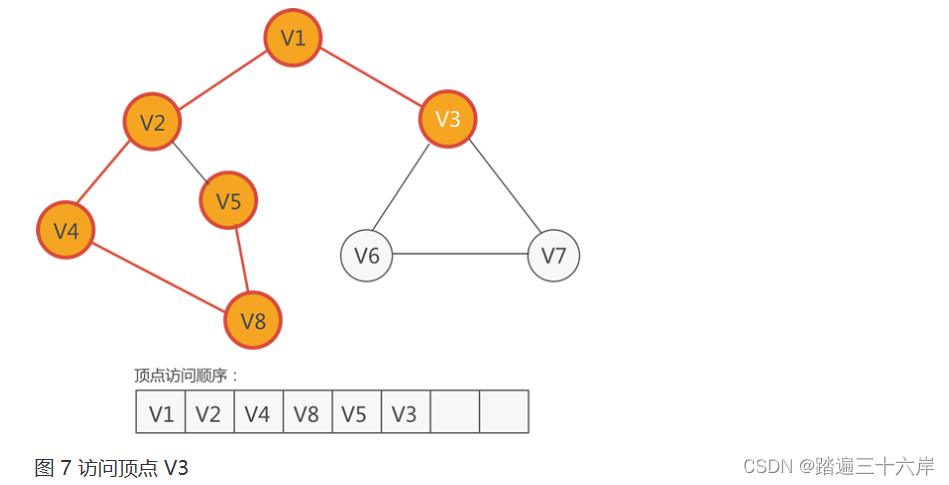
7 . 紧 V3 的顶点有三个,分别是 V1、V6 和 V7,尚未访问的有 V6 和 V7,因此从它们中任选一个,比如访问 V6,如下图所示:
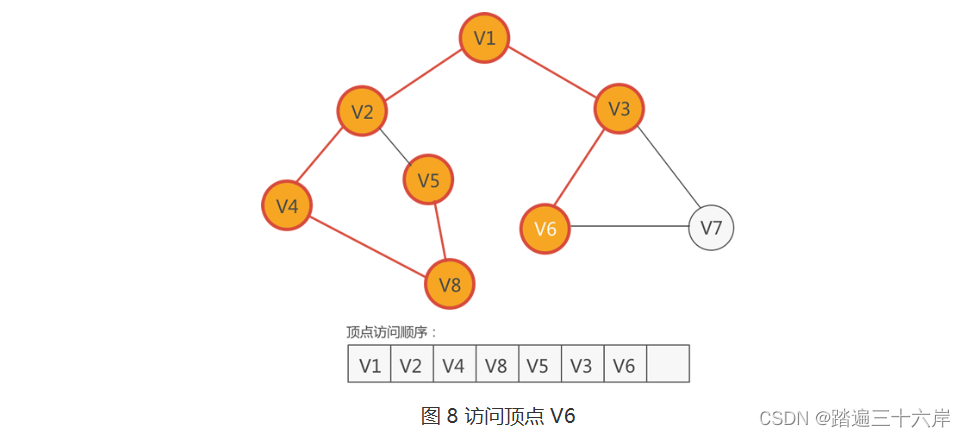
8 . 紧邻 V6 的顶点有两个,分别是 V3 和 V7,只有 V7 还没有访问,因此访问 V7,如下图所示:
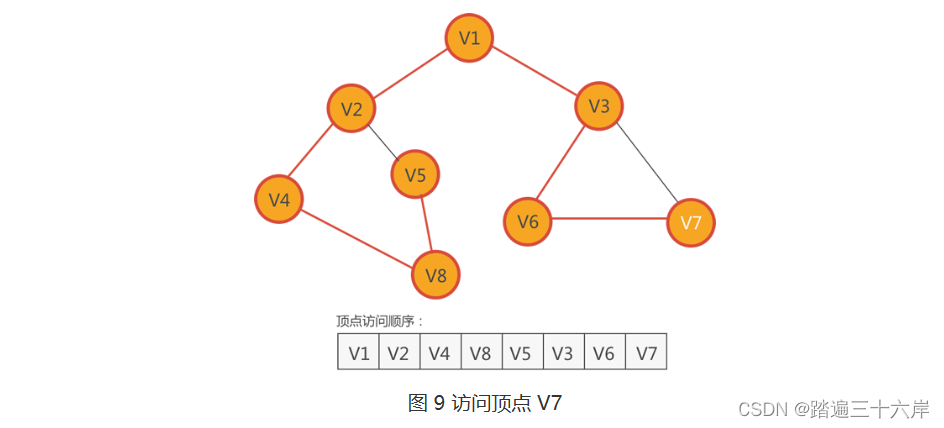
9 . 紧邻 V7 顶点有 V6 和 V3,但它们都已经访问过了,此时面临的情况和第 6 步完全一样,深度优先搜索算法的解决方法也是一样的:
- 从 V7 回退到 V6,依然找不到尚未访问的顶点
- 从 V6 回退到 V3,依然找不到尚未访问的顶点
- 从 V3 回退到 V1,依然找不到尚未访问的顶点
V1 是遍历图的起始顶点,回退到 V1 找不到尚未访问的顶点,意味着以 V1 顶点为突破口,能访问的顶点全部已经访问完了。这种情况下,深度优先搜索算法会从图的所有顶点中重新选择一个尚未访问的顶点,从该顶点出发查找尚未访问的其它顶点。
从图 9 可以看到,图中已经没有尚未访问的顶点了,此时深度优先搜索算法才执行结束
对于连通图来说,深度优先搜索算法从一个顶点出发就能访问图中所有的顶点。但是对于非连通图来说,深度优先搜索算法必须从各个连通分量中选择一个顶点出发,才能访问到所有的顶点。
所谓深度优先搜索,就是从图中的某个顶点出发,不停的寻找相邻的、尚未访问的顶点:
- 如果找到多个,则任选一个顶点,然后继续从该顶点出发
- 如果一个都没有找到,则回退到之前访问过的顶点,看看是否有漏掉的,假设从顶点 V 出发,则最终还会回退到顶点 V。此时,深度优先搜索算法会从所有顶点中重新找一个尚未访问的顶点,如果能找到,则以同样的方式继续寻找其它未访问的顶点;如果找不到,则算法执行结束。
通常情况下,深度优先搜索算法访问图中顶点的顺序是不唯一的,即顶点的访问序列可能有多种 ( >= 1)。
图的存储结构有很多种,大体上可以分为顺序存储和链式存储 (又细分为邻接表结构、十字链表结构和邻接多重表结构),各个存储结构有自己的特点。选用不同的存储结构,深度优先搜索算法的具体实现不同,但算法的思想是不变的。
图的广度优先遍历
广度优先搜索(Breadth First Search) 简称广搜或者 BFS,是遍历图存储结构的一种算法,既适用于无向图 (网),也适用于有向图 (网)。
所谓图的遍历,简单理解就是逐个访问图中的顶点,确保每个顶点都只访问一次。
首先通过一个样例,给大家讲解广度优先搜索算法是如何实现图的遍历的 .

使用广度优先搜索算法,遍历图 1 中无向图的过程是
1 . 初始状态下,图中所有顶点都是尚未访问的,因此任选一个顶点出发,开始遍历整张图。
比如从 V1 顶点出发,先访问 V1:

2 . 从 V1 出发,可以找到 V2 和 V3,它们都没有被访问,所以访问它们:

注意:本图中先访问的是 V2,也可以先访问 V3。当可以访问的顶点有多个时,访问的顺序是不唯一的可以根据找到各个顶点的先后次序依次访问它们。后续过程也会遇到类似情况,不再重复赘述。
3 . 根据图 3 中的顶点访问顺序,紧邻 V1 的顶点已经访问过,接下来访问紧邻 V2 的顶点从 V2 顶点出发,可以找到 V1、V4 和 V5,尚未访问的有 V4 和 V5,因此访问它们:
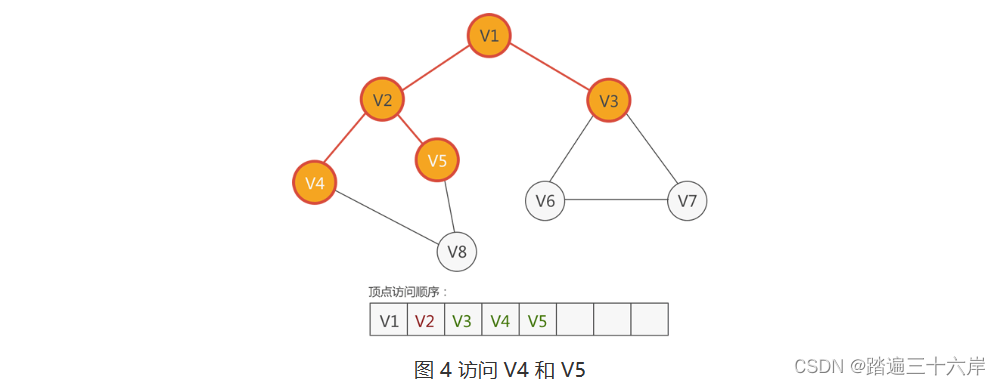
4 . 根据图 4 中的顶点访问顺序,接下来访问紧邻 V3 的顶点从 V3 顶点出发,可以找到 V1、V6 和 V7,尚未访问的有 V6 和 V7,因此访问它们:
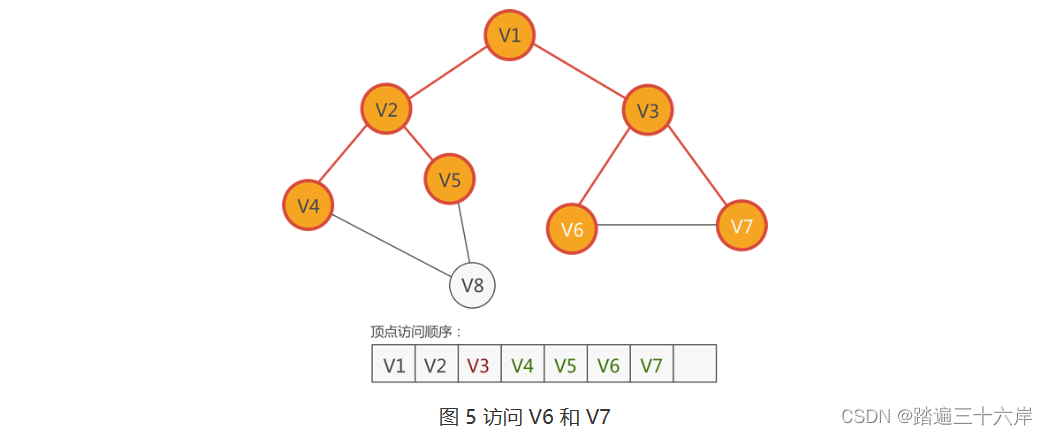
5 . 根据图 5 中的顶点访问顺序,接下来访问紧邻 V4 的顶点从 V4 顶点出发,可以找到 V2 和 V8,只有 V8 尚未访问,因此访问它:
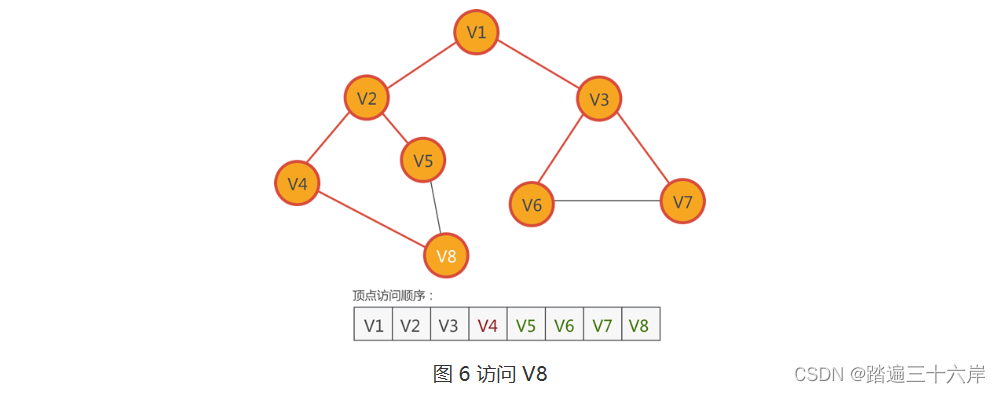
6 . 根据图 6 的顶点访问顺序,接下来访问紧邻 V5 的顶点
观察图 6 中的无向图不难发现,与 V5 紧的 V2 和 V8 都已经访问过,无法再找到尚未访问的顶点。此时,广度优先搜索算法会直接跳过 V5,继续从其它的顶点出发。
7 . 广度优先搜索算法先后从 V6、V7、V8 出发,寻找和它们紧邻、尚未访问的顶点,但寻找的结果都和 V5 一样,找不到符合要求的顶点。
8 . 自 V8 之后,访问序列中再无其它顶点,意味着从 V1 顶点出发,无法再找到尚未访问的顶点。这种情况下,广度优先搜索算法会从图的所有顶点中重新选择一个尚未访问的顶点,然后从此顶点出发,以同样的思路继续寻找其它尚未访问的顶点。
所谓广度优先搜索,就是从图中的某个顶点出发,寻找紧邻的、尚未访问的顶点,找到多少就访问多少然后分别从找到的这些顶点出发,继续寻找紧邻的、尚未访问的顶点。
当从某个顶点出发,所有和它连通的顶点都访问完之后,广度优先搜索算法会重新选择一个尚未访问的顶点(非连通图中就存在这样的顶点),继续以同样的思路寻找未访问的其它顶点。直到图中所有顶点都被访问,广度优先搜索算法才会结束执行。
这期就到这里 , 下期见!







![[python]matplotlib](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=matplotlib_files%2Fmatplotlib_86_2.png&pos_id=img-dQqTqhVb-1704115208460)


![[Mac软件]ColorWell For Mac 7.4.0调色板生成器](https://img-blog.csdnimg.cn/direct/b250db8b254a45ada7f4829020b819ff.png)