目录
437. 路径总和 III
深度优先遍历
前缀和优化
124. 二叉树中的最大路径和
437. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
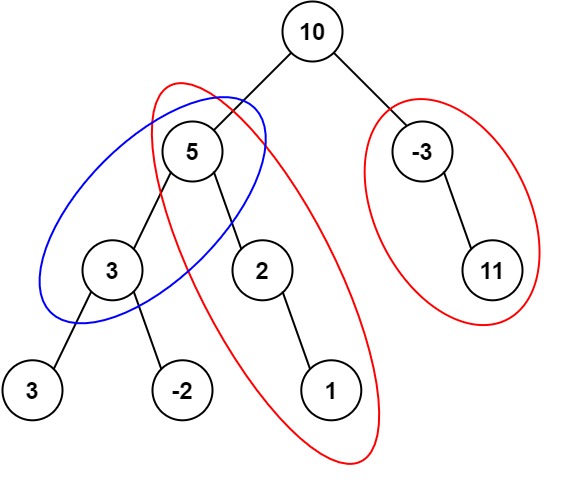
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -109 <= Node.val <= 109-1000 <= targetSum <= 1000
深度优先遍历
遍历每个节点,以每个节点为根节点统计所有路径和为targetSum情况
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if (root == null) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
}
public int rootSum(TreeNode root, int targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
if (val == targetSum) {
ret++;
}
ret += rootSum(root.left, targetSum - val);
ret += rootSum(root.right, targetSum - val);
return ret;
}
}前缀和优化
解法一中应该存在许多重复计算,我们现在定义:前缀和是一个数列的每一项索引从0开始,表示从第0项到当前项的和。在这个问题中,我们将前缀和应用于二叉树的路径上,即从根节点到当前节点的所有节点值的和。
-
初始化:创建一个哈希表
prefix来保存前缀和及其出现次数。为了处理从根节点开始的路径,我们提前在哈希表中设置前缀和0的计数为1。 -
递归遍历:使用深度优先搜索遍历二叉树。在每个节点处,计算从根节点到当前节点的前缀和。
-
查找当前路径和:检查当前的前缀和减去
targetSum的结果是否在之前的路径中已经出现过,也就是检查curr - targetSum是否在哈希表prefix中。如果是,说明存在一个子路径的和等于targetSum,将对应的次数添加到结果中。 -
更新哈希表:在访问节点之前,将当前前缀和的计数增加1,以表示这个前缀和现在被包含在路径中。
-
递归子节点:继续对左右子节点进行相同的处理。
-
回溯:在返回之前,需要将当前节点的前缀和的计数减1,因为当前节点即将被回溯,不应该计入其他路径(不存在以某个节点为根节点的路径所以要回溯避免影响其他路径)。
class Solution {
// 主函数
public int pathSum(TreeNode root, int targetSum) {
// 哈希表用于存储所有前缀和及其出现次数
Map<Long, Integer> prefix = new HashMap<Long, Integer>();
// 初始化:前缀和为0的路径有1条(空路径)
prefix.put(0L, 1);
// 开始深度优先搜索
return dfs(root, prefix, 0, targetSum);
}
// 辅助函数:深度优先搜索
public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
// 如果当前节点为空,则返回0,表示没有路径
if (root == null) {
return 0;
}
int ret = 0; // 用于记录路径数
curr += root.val; // 更新当前路径和
// 查找当前路径和减去目标值的结果是否在前缀和中出现过
// 出现过则表示找到了一条路径
ret = prefix.getOrDefault(curr - targetSum, 0);
// 更新前缀和中当前路径和的计数
prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);
// 递归地搜索左子树和右子树,并累加路径数
ret += dfs(root.left, prefix, curr, targetSum);
ret += dfs(root.right, prefix, curr, targetSum);
// 回溯:在返回之前,将当前节点的路径和的计数减1
// 因为当前节点即将被回溯,不应该计入其他路径
prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);
// 返回找到的路径总数
return ret;
}
}让我们通过一个具体的例子来说明回溯在前缀和算法中的应用。假设有以下二叉树:
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
并且我们要找的 targetSum 是8。我们将按照前缀和算法遍历这棵树。
-
开始于根节点 (10):
- 当前前缀和:
curr = 10 prefix = { (0,1) }(初始化,路径和为0出现了1次)
- 当前前缀和:
-
移动到左子节点 (5):
- 当前前缀和:
curr = 15 - 更新前缀和计数:
prefix = { (0,1), (15,1) }
- 当前前缀和:
-
继续到该节点的左子节点 (3):
- 当前前缀和:
curr = 18 - 更新前缀和计数:
prefix = { (0,1), (15,1), (18,1) }
- 当前前缀和:
-
进一步到该节点的左子节点 (3):
- 当前前缀和:
curr = 21 - 更新前缀和计数:
prefix = { (0,1), (15,1), (18,1), (21,1) }
- 当前前缀和:
-
回溯到节点 (3) 父节点 (3):
- 我们完成了节点 (3) 的所有子节点的遍历
- 当前前缀和:
curr = 18 - 回溯:
prefix = { (0,1), (15,1), (18,1) },移除之前节点 (3) 的前缀和
-
遍历节点 (3) 的右子节点 (-2):
- 当前前缀和:
curr = 16 - 更新前缀和计数:
prefix = { (0,1), (15,1), (18,1), (16,1) } - 回溯:
prefix = { (0,1), (15,1), (18,1) },完成节点 (-2) 的遍历,移除它的前缀和
- 当前前缀和:
-
回溯到节点 (5) 并转向它的右子节点 (2):
- 我们完成了节点 (5) 的左子树的遍历
- 当前前缀和:
curr = 15 - 回溯:
prefix = { (0,1), (15,1) },移除之前节点 (3) 和 (-2) 的前缀和 - 当前前缀和:
curr = 17(添加节点 (2)) - 更新前缀和计数:
prefix = { (0,1), (15,1), (17,1) } - 检查:
17 (当前前缀和) - 8 (targetSum) = 9,在prefix中没有9,所以没有发现新路径 - 遍历节点 (2) 的左子节点 (1)
- 当前前缀和:
curr = 18(添加节点 (1)) - 更新前缀和计数:
prefix = { (0,1), (15,1), (17,1), (18,1) } - 检查:
18 (当前前缀和) - 8 (targetSum) = 10,在prefix中有10(根节点的值),所以我们找到了一条路径: 10 → 5 → 2 → 1 - 回溯:完成节点 (1) 的遍历,回溯节点 (2)
-
最终回溯到根节点 (10) 并转向它的右子节点 (-3):
- 当前前缀和:
curr = 10 - 回溯:
prefix = { (0,1) },移除左子树的前
- 当前前缀和:
124. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
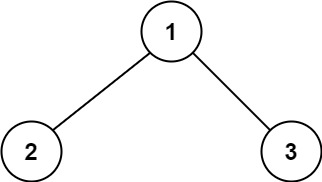
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
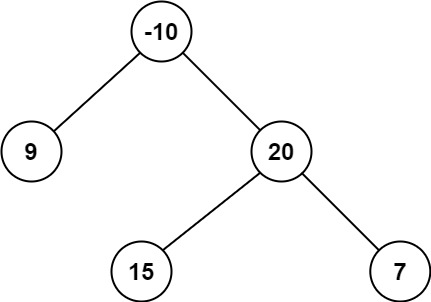
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
class Solution {
int maxSum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
maxGain(root);
return maxSum;
}
public int maxGain(TreeNode node) {
if (node == null) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时,才会选取对应子节点
int leftGain = Math.max(maxGain(node.left), 0);
int rightGain = Math.max(maxGain(node.right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node.val + leftGain + rightGain;
// 更新答案
maxSum = Math.max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node.val + Math.max(leftGain, rightGain);
}
}





![[Angular] 笔记 22:ElementRef](https://img-blog.csdnimg.cn/direct/bc4db18f90794a43a6b75909b76b37be.png)