【题目来源】
https://www.luogu.com.cn/problem/P1086
https://www.acwing.com/problem/content/description/420/

【题目描述】
在告示牌背后，路边真的有一块花生田，花生植株整齐地排列成矩形网格（如图 1）。
有经验的多多一眼就能看出，每棵花生植株下的花生有多少。
为了训练多多的算术，鲁宾逊先生说：“你先找出花生最多的植株，去采摘它的花生；然后再找 出剩下的植株里花生最多的，去采摘它的花生；依此类推，不过你一定要在我限定的时间内回到路边。”

我们假定多多在每个单位时间内，可以做下列四件事情中的一件：
（1）从路边跳到最靠近路边（即第一行）的某棵花生植株；
（2）从一棵植株跳到前后左右与之相邻的另一棵植株；
（3）采摘一棵植株下的花生；
（4）从最靠近路边（即第一行）的某棵花生植株跳回路边。

现在给定一块花生田的大小和花生的分布，请问在限定时间内，多多最多可以采到多少个花生？
注意：可能只有部分植株下面长有花生，假设这些植株下的花生个数各不相同。
例如在图 2 所示的花生田里，只有位于 (2,5),(3,7),(4,2),(5,4) 的植株下长有花生，个数分别为 13,7,15,9。
沿着图示的路线，多多在 21 个单位时间内，最多可以采到 37 个花生。

【输入格式】
输入文件的第一行包括三个整数，M,N 和 K，用空格隔开；表示花生田的大小为 M×N，多多采花生的限定时间为 K 个单位时间。
接下来的 M 行，每行包括 N 个非负整数，也用空格隔开；第 i+1 行的第 j 个整数 Pij 表示花生田里植株 (i,j) 下花生的数目，0 表示该植株下没有花生。

【输出格式】
输出文件包括一行，这一行只包含一个整数，即在限定时间内，多多最多可以采到花生的个数。

【数据范围】
1≤M,N≤20,
0≤K≤1000,
0≤Pij≤500

【输入样例】
6 7 21
0 0 0 0 0 0 0
0 0 0 0 13 0 0
0 0 0 0 0 0 7
0 15 0 0 0 0 0
0 0 0 9 0 0 0
0 0 0 0 0 0 0

【输出样例】
37

【算法分析】
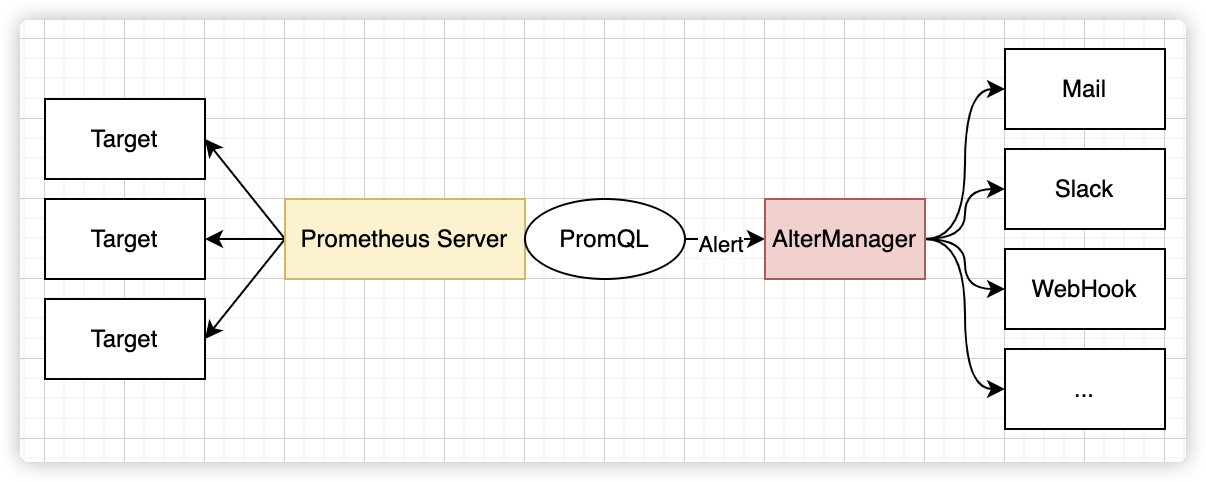
本题的一种实现方法需要按结构体某一字段对结构体数组进行排序，详见：
https://blog.csdn.net/hnjzsyjyj/article/details/120184972
例如，若自定义的结构体 Person 的内容如下：

struct Person {
    string name;
    int age;
    float height;
};

则可自定义的递增函数 up()、递减函数 down() 的内容如下：

int up(Person u,Person v) { //ascending by height
    if(u.height==v.height) return u.name<v.name; //If equal,ascending by name
    return u.height<v.height;
}
 
int down(Person u,Person v) { //descending by height
    if(u.height==v.height) return u.name>v.name; //If equal,descending by name
    return u.height>v.height;
}

若 p 为结构体数组，则在主函数中调用递增函数 up()、递减函数 down() 的代码如下：

sort(p,p+n,up); //Sort the structured array p by ascending field height
 
sort(p,p+n,down); //Sort the structured array p by descending field height

【算法代码】

#include <bits/stdc++.h>
using namespace std;

const int maxn=500;

struct Node {
    int x,y,num;
} a[maxn];

bool down(Node u,Node v) {
    return u.num>v.num;
}

int cnt,dis,ans;

int main() {
    int m,n,k;
    cin>>m>>n>>k;
    for(int i=1; i<=m; i++) {
        for(int j=1; j<=n; j++) {
            a[cnt].x=i;
            a[cnt].y=j;
            cin>>a[cnt].num;
            if(a[cnt].num) cnt++;
        }
    }

    sort(a,a+cnt,down);

    for(int i=0; i<cnt; i++) {
        if(i==0) dis+=a[i].x+1;
        else dis+=abs(a[i].x-a[i-1].x)+abs(a[i].y-a[i-1].y)+1;
        if(dis+a[i].x<=k) ans+=a[i].num;
    }
    cout<<ans<<endl;

    return 0;
}


/*
in:
6 7 21
0 0 0 0 0 0 0
0 0 0 0 13 0 0
0 0 0 0 0 0 7
0 15 0 0 0 0 0
0 0 0 9 0 0 0
0 0 0 0 0 0 0

out:
37
*/

【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/120184972
https://blog.csdn.net/hnjzsyjyj/article/details/134920069