文章目录
- 1 好的关系设计的特征
- 2 函数依赖关系
- 3 Normal Forms 规范形式
- 3.1 一二三范式
- 3.1.1 基本概念
- 3.1.2 判断是否满足3NF
- 3.2 BCNF
- 3.2.1 基本概念
- 3.2.2 判断是否满足BCNF
- 3.2.3 分解得到BCNF
- 4 属性集闭包和正则覆盖
- 4.1 属性集闭包求法
- 4.2 属性集闭包应用
- 4.2.1 测试某个属性集是否为超键
- 4.2.2 测试一个属性是否无关属性
- 4.3正则覆盖Canonical Cover
1 好的关系设计的特征
好的设计
要避免冗余
要避免更新、删除或者插入异常
那么为了在设计中进行好的设计
就应该合理的分解表格
但是有些时候分解会造成一些不好的影响——会产生有损分解或者无损分解
所什么是无损分解,什么是有损分解?
判断方式一
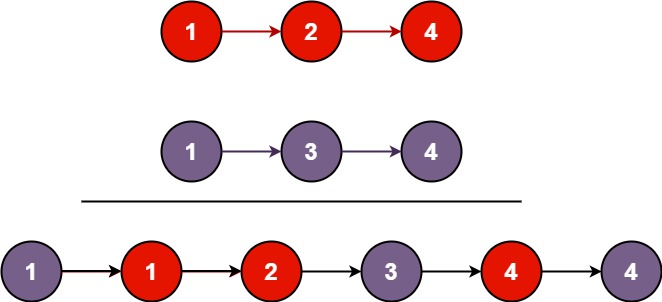
对于关系R,分解为R1和R2
讲两个分解后的表R1,R2做自然连接,如连接后和原来表R相等,则是无损分解。
如果自然连接后产生了原理表R没有的元组,则为有损分解
判断方式二
对于关系R,分解为R1和R2
如果R1和R2的交集是R1或者R2其中之一的超键则为无损分解,否则为有损分解
2 函数依赖关系
函数依赖 Functional Dependencies,就是初中高中学习的判断一个对应关系是否为函数
很简单,就是一个x对应唯一一个y
需要先着重理解两个概念
平凡函数依赖 Trivial Functional Dependencies
如果x->y,即y是x的函数,同时y又是x的子集,那么就说x到y是平凡函数依赖
平凡的含义就是显而易见的,为什么叫显而易见呢?子集我们可以理解为信息的一部分,信息相对原来变少了,那么因为知道更多的信息肯定可以推出更少的信息的,所以这个x-》y的函数依赖关系是显而存在的
举这样一个例子
(学生ID,姓名)->(姓名)
其中x是(学生ID,姓名),y是(姓名)
那么如果知道了学生ID,姓名,肯定可以得到唯一的姓名
非平凡函数依赖
而如果y不是x的子集,那么就不那么明显了,所以是非平凡函数依赖
再理解两个概念,部分函数依赖和完全函数依赖
理解部分函数依赖和完全函数依赖
部分函数依赖(Partial Functional Dependency)(候选码): 部分函数依赖是指在关系中,
比如x->y的函数依赖,y只依赖x的一部分,那么则是部分函数依赖,x还可以再拆分
举个例子,假设有一个包含以下属性的关系表:
- 学生ID(StudentID)
- 课程号(CourseID)
- 学生姓名(StudentName)
(学生ID,课程号)是可以推出学生姓名的
而只有学生ID也可以推出决定学生姓名,所以可以继续拆分,为部分函数依赖,换句话说x的子集也能推出决定右边
完全函数依赖(Full Functional Dependency)(超码):完全函数依赖是指在关系中,
比如x->y的函数依赖,y依赖x的全部,那么则是全部函数依赖,x不可以再拆分
换句话说x的子集不能推出决定右边
包含在任何一个候选码中的属性 ,称为主属性(Prime attribute)
不包含在任何候选码中的属性称为非主属性(Nonprime attribute)

总结来看:我们更期望非平凡函数依赖和完全函数依赖
函数依赖的闭包 Closure of Functional Dependencies
函数依赖闭包表示为 F + F^+ F+
函数依赖的闭包是一个属性集合,它包含了一个给定的属性集合关于另一个属性集合的所有可能依赖,所有的可能的函数关系
如何求函数依赖的闭包
利用
Armstrong’s Axioms 阿姆斯特朗公理
阿姆斯特公理有三条
- 自反率(Reflexivity Axiom): 如果X是一个属性集合,那么X的任何子集都可以推出X,表示为X → X。这意味着一个属性集合的所有子集都具有相同的函数依赖。
- 扩展律(Augmentation Axiom): 如果X → Y,并且Z是一个属性集合,那么XZ → YZ。这个公理表示如果一个属性集合X决定另一个属性集合Y,那么在X的基础上添加属性Z也会决定Y。
- 传递律(Transitivity Axiom): 如果X → Y和Y → Z,那么X → Z。这个公理表示如果一个属性集合X决定另一个属性集合Y,同时Y又决定另一个属性集合Z,那么X也会决定Z。
另外的
-
Union Rule(并集规则): Union Rule 允许我们将两个函数依赖合并成一个更大的函数依赖。规则表述如下:
如果 X → Y1 和 X → Y2,那么 X → (Y1 ∪ Y2)。
这意味着如果属性集合 X 决定属性集合 Y1,同时 X 也决定属性集合 Y2,那么 X 也决定属性集合 (Y1 ∪ Y2),也就是 Y1 和 Y2 的并集。
-
Splitting Rule(拆分规则): Splitting Rule 允许我们拆分函数依赖,将一个函数依赖分成两个更小的函数依赖。规则表述如下:
如果 X → (Y1 ∪ Y2),那么 X → Y1 和 X → Y2。
这意味着如果属性集合 X 决定属性集合 (Y1 ∪ Y2),那么 X 也分别决定属性集合 Y1 和属性集合 Y2。这可以用于将一个大的函数依赖分解成多个小的函数依赖。
-
Pseudotransitivity Rule(伪传递规则): Pseudotransitivity Rule 允许我们在两个已知的函数依赖关系之间推导出一个新的函数依赖。规则表述如下:
如果 X → Y1 和 Y1Z → Y2,那么 XZ → Y2。
这意味着如果属性集合 X 决定属性集合 Y1,同时 Y1Z 决定属性集合 Y2,那么属性集合 XZ 也决定属性集合 Y2。这个规则有点类似于传递性,但不完全相同,因此称为伪传递规则。
通过上面的,我们可以求得一个函数依赖关系的闭包,我从网上找到了一道题,但感觉求这个意义不大

3 Normal Forms 规范形式
3.1 一二三范式
3.1.1 基本概念
规范形式(Normalization Forms,通常缩写为NF)是数据库设计中的一组标准,用于确保数据库表的结构满足一定的标准,以提高数据的一致性、避免数据冗余,并提高数据库性能。最常见的规范形式包括第一范式(1NF)、第二范式(2NF)和第三范式(3NF)。
- 第一范式(1NF):
- 第一范式要求数据库表中的每个列都包含不可分割的、原子的数据,也就是每个单元格只包含一个值。此外,表中的每个行都应具有唯一的标识,通常通过一个主键来实现。1NF消除了重复的列和组合列。
- 第二范式(2NF):
- 第二范式要求在1NF的基础上,确保非主键属性完全依赖于主键。这意味着非主键属性不会部分依赖主键,也就是没有部分函数依赖。如果存在部分函数依赖,需要将表进行拆分,以确保每个非主键属性都依赖于整个主键。通常,2NF适用于具有复合主键的表。
- 第三范式(3NF):
- 第三范式要求在2NF的基础上,消除传递依赖。传递依赖指的是非主键属性依赖于主键以外的非主键属性。如果一个非主键属性依赖于另一个非主键属性,而这个属性又依赖于主键,就存在传递依赖。为了满足3NF,需要将数据库表进行拆分,以确保每个非主键属性只依赖于主键。
实际上3NF达到的效果就是 尽可能保证 非主键属性完全依赖于主建且只依赖于主键
规范形式的目标是减少数据冗余、提高数据一致性,并简化数据库结构,以便更容易维护和查询数据。虽然1NF、2NF和3NF是最常见的规范形式,但还有更高级别的规范形式,如巴斯-科德范式(BCNF)和第四范式(4NF),它们进一步强化了数据库设计的要求。
总结
第一范式:简单说 列不能再分
第二范式:简单说 建立在第一范式基础上,消除部分依赖
第三范式:简单说 建立在第二范式基础上,消除传递依赖。
BCNF是对3NF的改进,消除了对主键子集的依赖
3.1.2 判断是否满足3NF
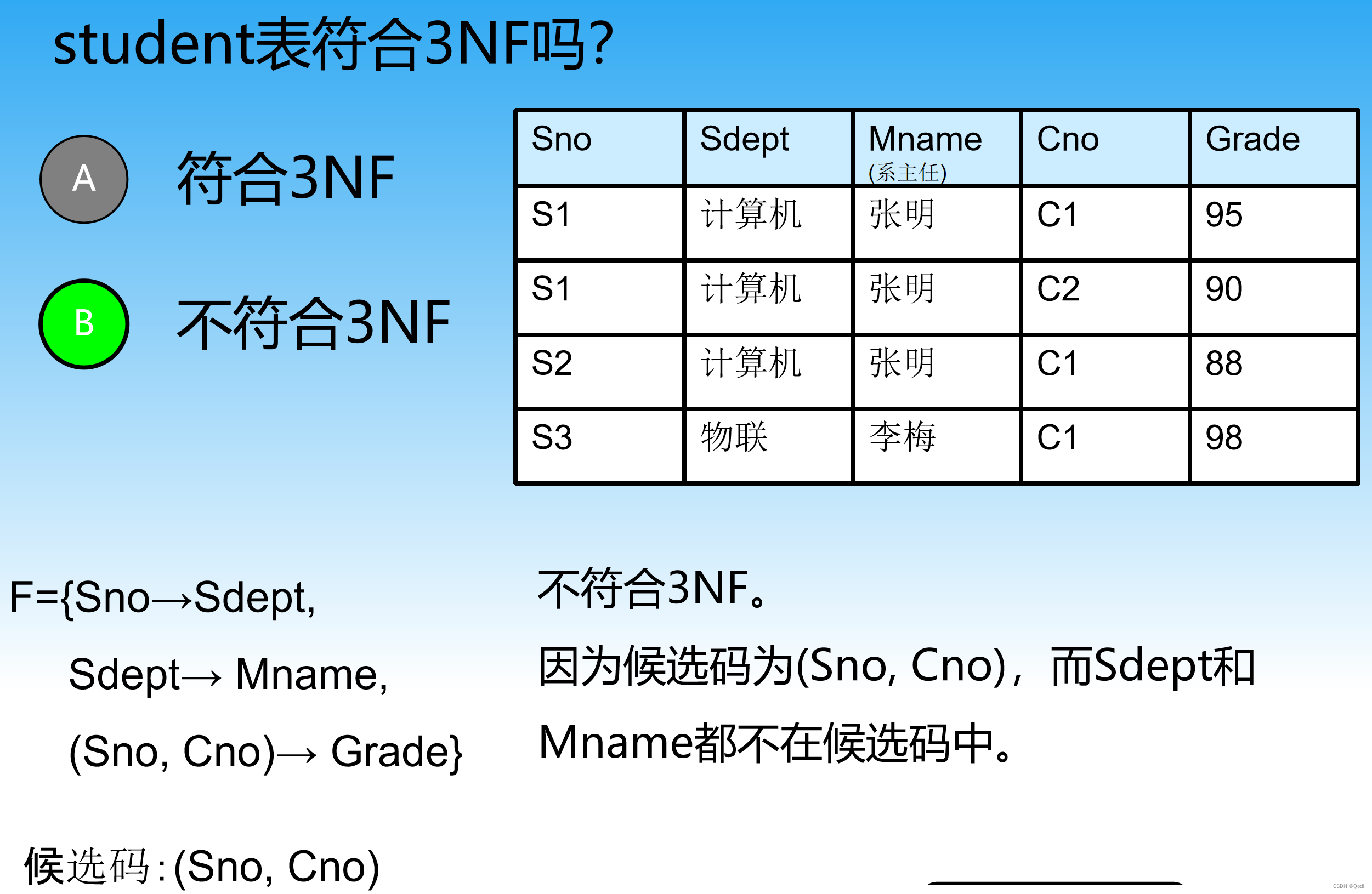
3.2 BCNF
3.2.1 基本概念
Boyce-Codd Normal Form(巴斯-科德范式(BCNF))是Third Normal Form 的一种扩展,因此有时候也被称为3.5范式。
- Boyce-Codd Normal Form(巴斯-科德范式)
- 在3NF基础上,任何非主属性不能对主键子集依赖(在3NF基础上消除对主码子集的依赖)
- 巴斯-科德范式(BCNF)是第三范式(3NF)的一个子集,即满足巴斯-科德范式(BCNF)必须满足第三范式(3NF)。通常情况下,巴斯-科德范式被认为没有新的设计规范加入,只是对第二范式与第三范式中设计规范要求更强,因而被认为是修正第三范式,也就是说,它事实上是对第三范式的修正,使数据库冗余度更小。这也是BCNF不被称为第四范式的原因。某些书上,根据范式要求的递增性将其称之为第四范式是不规范,也是更让人不容易理解的地方。
3.2.2 判断是否满足BCNF
判断每一个是否是超码,有一个不是就不是
a is a superkey for R
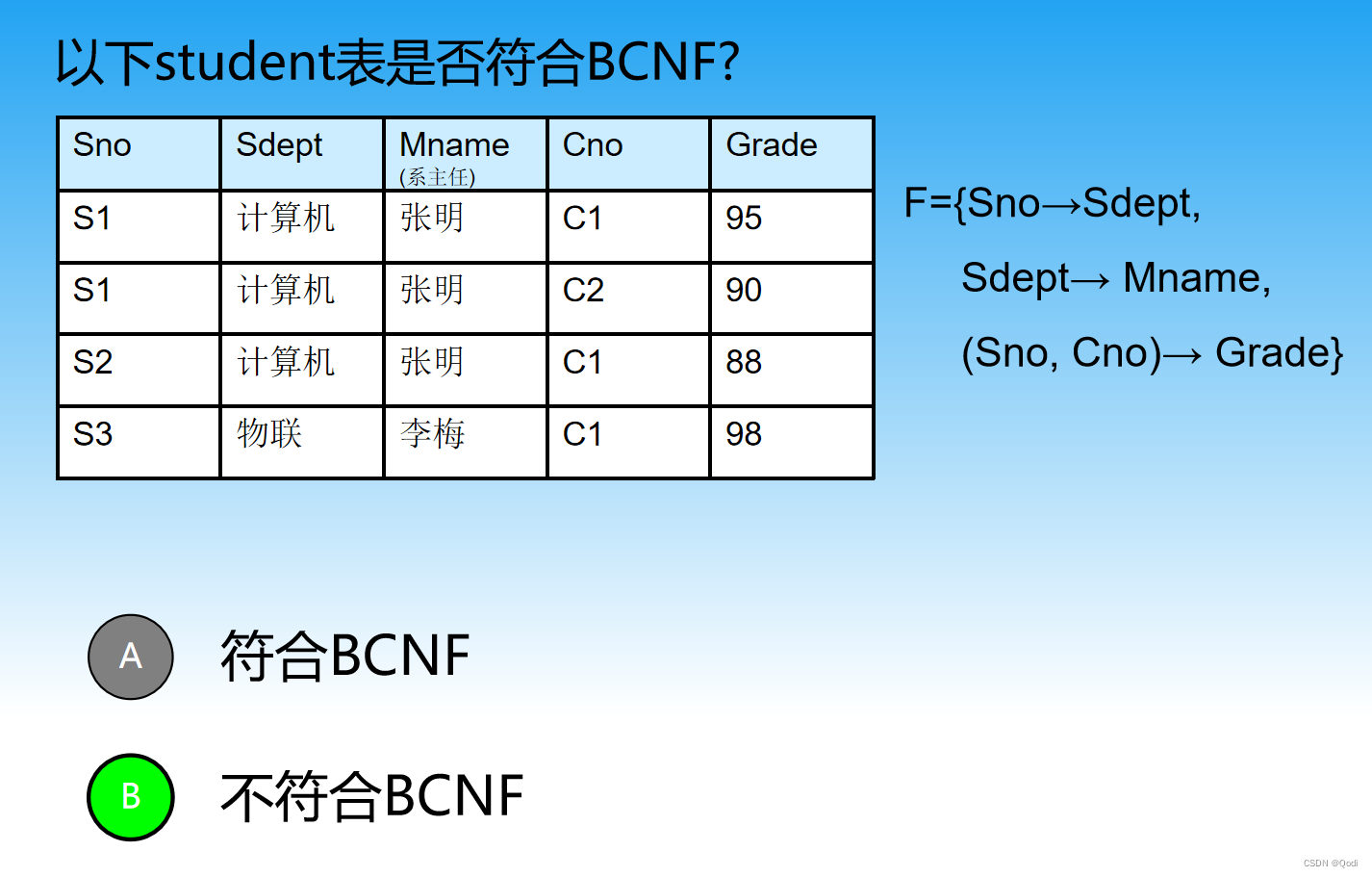
因为Sno→Sdept中Sno不是超码
Sdept→Mname中Sdept不是超码
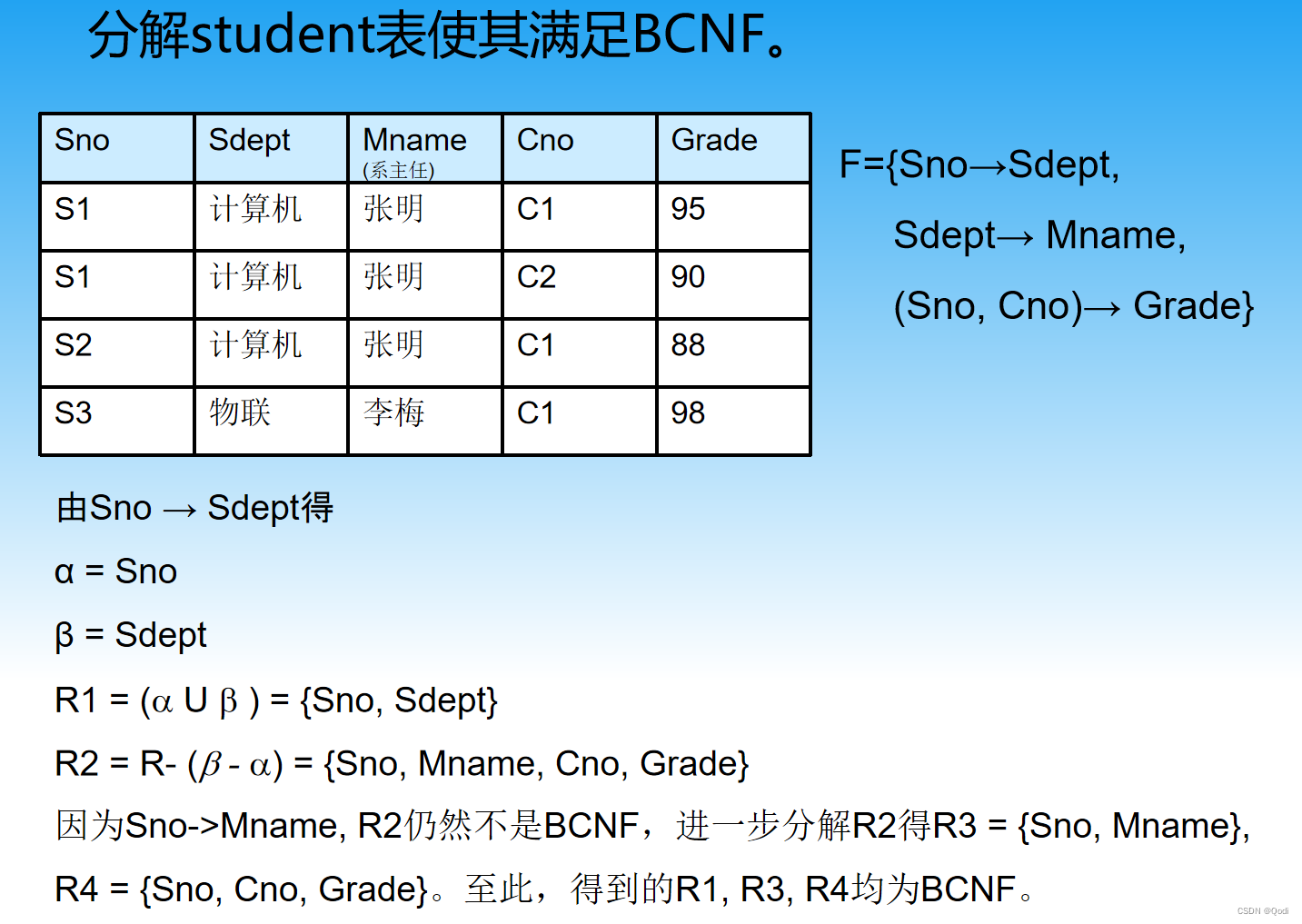
3.2.3 分解得到BCNF
怎么分解得到呢?
对于x->y
分解为x并y和R-(y-x)
4 属性集闭包和正则覆盖
4.1 属性集闭包求法
ps:可以理解为X+表示所有X可以决定的属性
求取属性集闭包的步骤:
设要求的闭包属性集是Y,把Y初始化为X.
检查函数依赖集F中的每个函数依赖A->B,如果属性集A中的所有属性都在Y中,而B中有属性不在Y中,则将其加入到Y中。
重复第二步,直到没有属性可以添加到Y中为止。最后得出的Y就是X+。
*例子:*设有关系模式R(M,N,X,Y,Z)其依赖集F={M->H,H->Z,Y->Z,N->Y,Z->M}。求M+,MH+
第一步:设要求的闭包属性集是Y,把Y初始化为X.
令X={M},我们先看M->H,由于函数依赖M->H左边的所有属性都在X中,而右边H不在X中,所以可以把H添加到X 中,此时X={M,H}
然后按照顺序我们再看H->Z,我们不难发现函数依赖H->Z左边的所有属性都在X中,右边的属性Z又不在X中,仍旧添加,这时X={M,H,Z}
下一个
Y->Z,可以发现Y属性不在X中,条件不满足
N->Y,可以发现N属性不在X中,条件不满足
Z->M,Z属性在X中条件满足,但右边M也在X中条件不满足。
属性判断完 ,那么属性M的闭包:M+=MHZ。
4.2 属性集闭包应用
4.2.1 测试某个属性集是否为超键
他的闭包如果包含所有属性,则为超集
4.2.2 测试一个属性是否无关属性
右边多余
如果前面的属性集闭包可以包括后面的,即可以删除无关的

左边多余
还可以计算函数依赖闭包,测试函数依赖是否成立
范式判断的三个步骤以及各个范式标准(1NF,2NF,3NF,BCNF,4NF)_如何判断1nf2nf3nf和bcnf-CSDN博客
4.3正则覆盖Canonical Cover
一.使用合并律将所有左部相同的函数依赖合并成一个
设有一函数依赖集F,其中有{A→B,A→E,……},则将这两个函数依赖合并为{A→BE,……}
二.在合并后的函数依赖集中寻找一个无关属性,将它删除
重复一二,直到每个元素都不是无关元素,无法再删,故解得正则覆盖
例题可以参考
正则覆盖的求法与判断属性是否冗余-CSDN博客