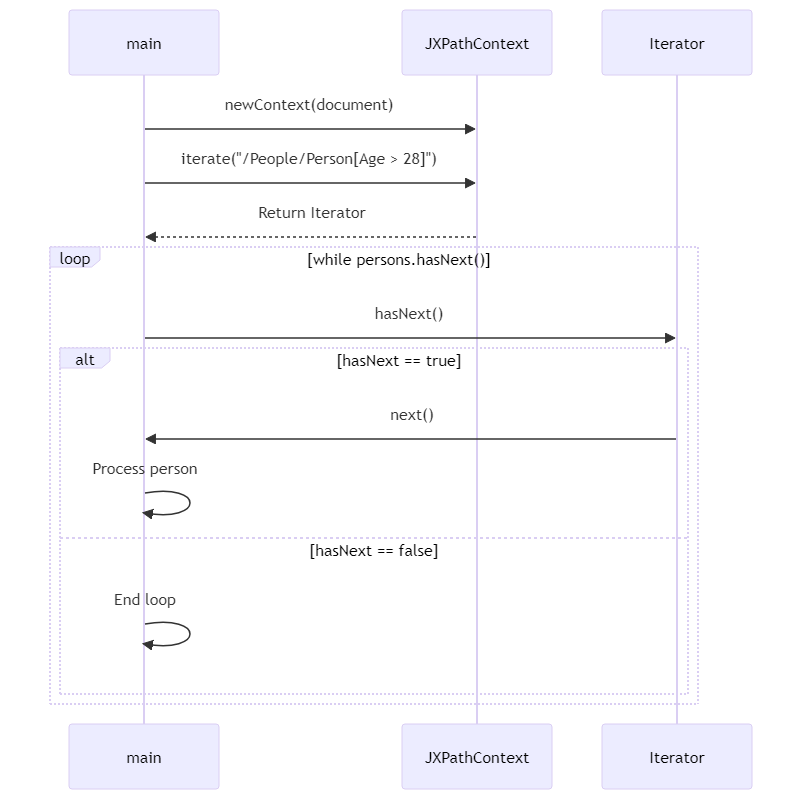
校课程的简单实验报告。
算法设计与分析实验报告-递归与分治策略
算法设计与分析实验报告-动态规划算法
算法设计与分析实验报告-贪心算法
dijkstra迪杰斯特拉算法(邻接表法)
算法设计与分析实验报告-回溯法
算法设计与分析实验报告-分支限界法
算法设计与分析实验报告-分治法相关练题
北京大学出版社-算法设计与分析
一、实验目的
1.理解贪心算法的概念;
2.掌握贪心算法的基本要素;
3.掌握设计贪心算法的步骤和策略。
二、实验内容
使用贪心法求解以下问题,要求给出程序代码,并编译运行程序:
1.P118习题2。
2.P118习题5。
三、实验环境
1. 使用的操作系统及版本:
Windows 10
2. 使用的编译系统及版本:
CLion 2022.2.4
四、实验步骤及说明
1、P118习题2
对于用邻接链表表示的有向无环图,设计一个解单起点最短路径问题的线性算法。
dijkstra迪杰斯特拉算法(邻接表法)
代码如下:
//
// Created by GiperHsiue on 2022/11/27.
//
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
#define INFINE 99999 // 定义最大
// 邻接表
struct ArcNode // 边信息
{
int adjvex; //有向边的 目标顶点 下标(从1开始)
int weight; //边的权值
struct ArcNode *next; //邻接表, 指向下一个邻接边信息
};
struct VertexNode // 顶点
{
int vertex; //顶点下标(1 ~)
ArcNode *firstedge; // 有向边信息节点指针(源为vertex)
};
struct AdjList // 图
{
vector<VertexNode> adjlist; //顶点数组
int vexnum; //顶点数
int arcnum; //边数
};
// 图的初始化
void createGraph(AdjList& G){
cout << "输入顶点数 边数: " << endl;
cin >> G. vexnum >> G. arcnum;
// 初始化G的顶点数组
for(int i = 0; i <= G. vexnum; i ++){ // 下标从1开始, 所以初始化vexnum + 1个顶点(0无作用)
VertexNode* tmp = new VertexNode;
tmp->vertex = i, tmp->firstedge = nullptr;
G. adjlist. emplace_back(*tmp);
}
//边信息
// n1: 源顶点 n2: 目标顶点 we: 权重(距离)
int n1, n2, we;
cout << "输入边信息: (a b we): " << endl; // a -> b weight: we
for(int i = 0; i < G. arcnum; i ++){
cin >> n1 >> n2 >> we;
// 初始化一个边节点, 目标顶点为n2
ArcNode* tmp = new ArcNode;
tmp->adjvex = n2, tmp->weight = we;
// 头插法 将边信息节点插入
// 节约时间(尾插要一直遍历到尾部插入)
tmp->next = G. adjlist[n1]. firstedge;
G. adjlist[n1]. firstedge = tmp;
}
}
// 获取两顶点之间权重weight(距离)
int getWeight(AdjList& G, int n1, int n2){
if(n1 == n2) return 0;
ArcNode* tmp = G. adjlist[n1]. firstedge;
while(tmp){
if(tmp->adjvex == n2) return tmp->weight;
tmp = tmp->next;
}
// 两点之间没有边, 返回INFINE
return INFINE;
}
void Dijkstra(AdjList& G, int ear, vector<int>& prev, vector<int>& dist){
// 初始化
// flag数组记录 某点是否纳入已找到点集合
// prev数组记录 前驱顶点下标
// dist数组记录 从源顶点ear 到 i顶点的最短路径
vector<bool> flag (G. adjlist. size() + 1, false);
for(int i = 1; i <= G. vexnum; i ++) dist[i] = getWeight(G, ear, i), prev[i] = ear;
flag[ear] = true, prev[ear] = 0;
// 开始
for(int i = 2; i <= G. vexnum; i ++){
int pos = 1; // 未纳入的距离最小的顶点
int weiMin = INFINE;
for(int j = 1; j <= G. vexnum; j ++){
if(!flag[j] && dist[j] < weiMin){
weiMin = dist[j], pos = j;
}
}
flag[pos] = true;
for(int j = 1; j <= G. vexnum; j ++){
if(!flag[j]){ // 未纳入点集中, 找到pos到这些点的距离, 与dist数组比较是否更新
int tmpWei = getWeight(G, pos, j);
if(tmpWei != INFINE) tmpWei = tmpWei + weiMin; // 两点距离应该为ear -> pos -> j
if(tmpWei < dist[j]) {
dist[j] = tmpWei; // 距离更小则更新dist
prev[j] = pos; // 前顶点更新为pos
}
}
}
}
}
// 找路径
void pathDist(vector<int>& prev, vector<int>& dist, int ear){
// prev数组中为1有2种情况(djikstra初始化过程的时候全赋值为1, 后续一直未改变):
// 1: 从ear到 顶点 只有 ear -> 顶点 这一条路最短
// 2: 无法从ear到达的顶点
for(int i = 1; i <= prev. size() - 1; i ++){
stack<int> trace;
if(ear == i) continue;
cout << ear << " 到 " << i ;
// 无连通
if(dist[i] == INFINE) {
cout << "无连通" << endl;
continue;
}
cout << "最短距离: " << dist[i] << " 最短路径: ";
int tmp = i;
while(tmp){ // 源顶点prev是0
trace. push(tmp);
tmp = prev[tmp];
}
// 开始出栈, 栈顶一定是ear源顶点
cout << trace. top();
trace. pop();
while(!trace. empty()){
cout << " -> " << trace. top();
trace. pop();
}
cout << endl;
}
}
int main(){
AdjList G;
createGraph(G);
// prev数组记录 前驱顶点下标
vector<int> prev (G. vexnum + 1, 0);
// dist数组记录 从源顶点ear 到 i顶点的最短路径
vector<int> dist (G. vexnum + 1, INFINE);
// 从源点ear 出发, 到达其余所有点的最短路径
cout << "输入源顶点ear: ";
int ear;
cin >> ear;
Dijkstra(G, ear, prev, dist);
pathDist(prev, dist, ear);
return 0;
}测试如下:
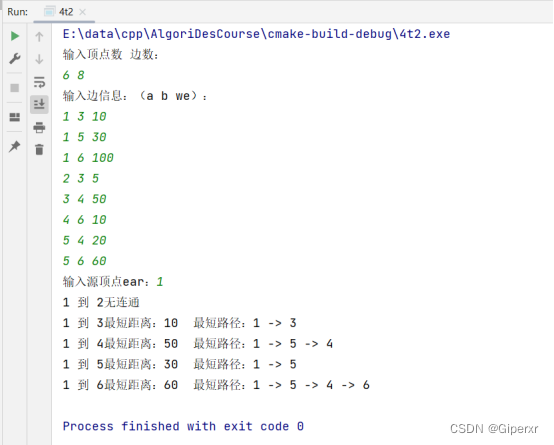
- P118习题5 小船过河问题
一群人划船过河,河边只有一条船,这条船可以容纳两个人,船过河后需要一人将船开回,以便所有人都可以过河,每个人过河速度不一样,两个人过河速度取决于慢的那个人,请问最少需要多久让所有人过河?
//
// Created by GiperHsiue on 2022/11/27.
//
// 小船过河问题
#include <iostream>
#include <vector>
using namespace std;
// 归并排序
void mergeSort(vector<int>& num, int l, int r){
if(l >= r) return;
int mid = l + (r - l) / 2;
mergeSort(num, l, mid), mergeSort(num, mid + 1, r);
int a = l, b = mid + 1, k = 0;
vector<int> tmp (r - l + 1, 0);
while(a <= mid && b <= r){
if(num[a] <= num[b]) tmp[k++] = num[a++];
else tmp[k++] = num[b++];
}
while(a <= mid) tmp[k++] = num[a++];
while (b <= r) tmp[k++] = num[b++];
for(int i = 0, j = l; j <= r; i ++, j ++) num[j] = tmp[i];
}
int calTime(vector<int>& num){
int cnt = num. size(), res = 0;
while(cnt > 3){
int tmp1 = num + 2 * num + num[cnt - 1];
int tmp2 = 2 * num + num[cnt - 1] + num[cnt - 2];
res += min(tmp1, tmp2);
cnt -= 2;
}
if(cnt == 2) res += num;
if(cnt == 3) res += num + num + num;
return res;
}
int main(){
int n;
cin >> n;
vector<int> people(n, 0);
for(auto &x: people) cin >> x;
mergeSort(people, 0, n - 1);
cout << "过河最少时间: " << calTime(people) << endl;
return 0;
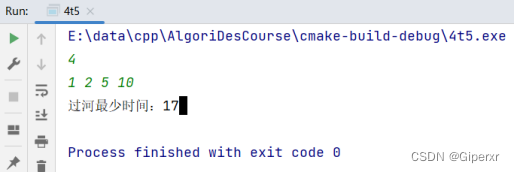
}代码如下:
测试如下:
五、实验小结及思考
通过本次实验对于贪心算法有了进一步的认识与理解,并运用贪心思维解决实际问题,理解贪心算法的概念,掌握贪心算法的基本要素,掌握设计贪心算法的步骤和策略。