前言
数学规划是一种数学优化方法,主要是寻找变量的取值在特定的约束情况下,使我们的决策目标得到一个最大或者最小值的决策。
使用数学规划的方法我们需要确定问题的目标、约束、变量的取值范围,然后进行数学建模,将数学公式转化为代码进行求解,得到的结果就是我们的最优决策。而优化求解器可以帮助我们求解大规模数据的数学规划问题。
数学规划的类型
数学规划的种类繁多,常见的有线性规划、整数规划、非线性规划、动态规划等。不同类型的规划适用于不同的实际问题,选择合适的规划方法可以提高问题求解的效率和准确性。
MindOpt优化求解器是阿里巴巴达摩院决策智能实验室研发的一款国产求解器,目前求解线性规划的能力十分强大,混合整数线性规划在第五届电力调度AI大赛中斩获冠军,还支持非线性规划中的凸二次规划、半定规划。
实际生活中我们遇到的问题种类更加丰富,例如非线性规划、混合整数非线性规划、约束规划、二次规划等。这些问题MindOpt就无法求解了吗?让我们接着看下文
实际应用
MAPL建模语言调用其他求解器
虽然MindOpt优化求解器当前还不支持这些功能,但MindOpt Studio 云上建模求解平台上可以使用MindOpt APL建模语言一行代码调用其他求解器进行求解。
MAPL支持调用多种优化求解器,包含商用求解器和开源求解器。
建模后可一行代码就切换求解器,如下,求解器名称均采用小写字母:
option solver mindopt; # (可选)指定求解用的求解器,默认是MindOpt
solve;
支持的调用的求解器如下:
| 开源求解器 | 描述 | 适合问题 |
|---|---|---|
| Ipopt | 来自COIN-OR, Eclipse Public License,可获取源码 https://github.com/coin-or/Ipopt | Nonlinear optimization (NLP) |
| Cbc | 来自COIN-OR, Eclipse Public License,可获取源码 https://github.com/coin-or/Cbc | Mixed integer linear programming(MILP) |
| Gecode | https://www.gecode.org/,MIT license,可获取源码https://github.com/Gecode/gecode | Constraint solver (约束规划) |
| Bonmin | 来自COIN-OR, Eclipse Public License,可获取源码:https://github.com/coin-or/Bonmin | Mixed-Integer Nonlinear Programming(MINLP) |
| HiGHS | https://highs.dev,MIT license,可获取源码https://github.com/ERGO-Code/HiGHS | large-scale sparse linear programming (LP), mixed-integer programming (MIP), and quadratic programming (QP) |
| Couenne | https://www.coin-or.org/Couenne/,来自COIN-OR, Eclipse Public License,可获取源码https://www.coin-or.org/download/source/ | Mixed-Integer Nonlinear Programming(MINLP) |
| JaCoP | GNU Affero General Public License,可获取源码:https://github.com/radsz/jacop | Constraint Programming(约束规划) |
支持的其他求解器可以查看文档
命令行模式调用
建模语言,又是一个新的知识!无论是否简单,都需要进行学习,那么有什么好的方法,或者更大众方法解决呢?MindOpt Studio 云上建模求解平台还提供了命令行调用其他求解器的功能,只需要将nl文件或者mps文件上传至平台的Notebook,然后输入求解器的名字以及文件名即可求解非线性规划、混合整数非线性规划等问题。
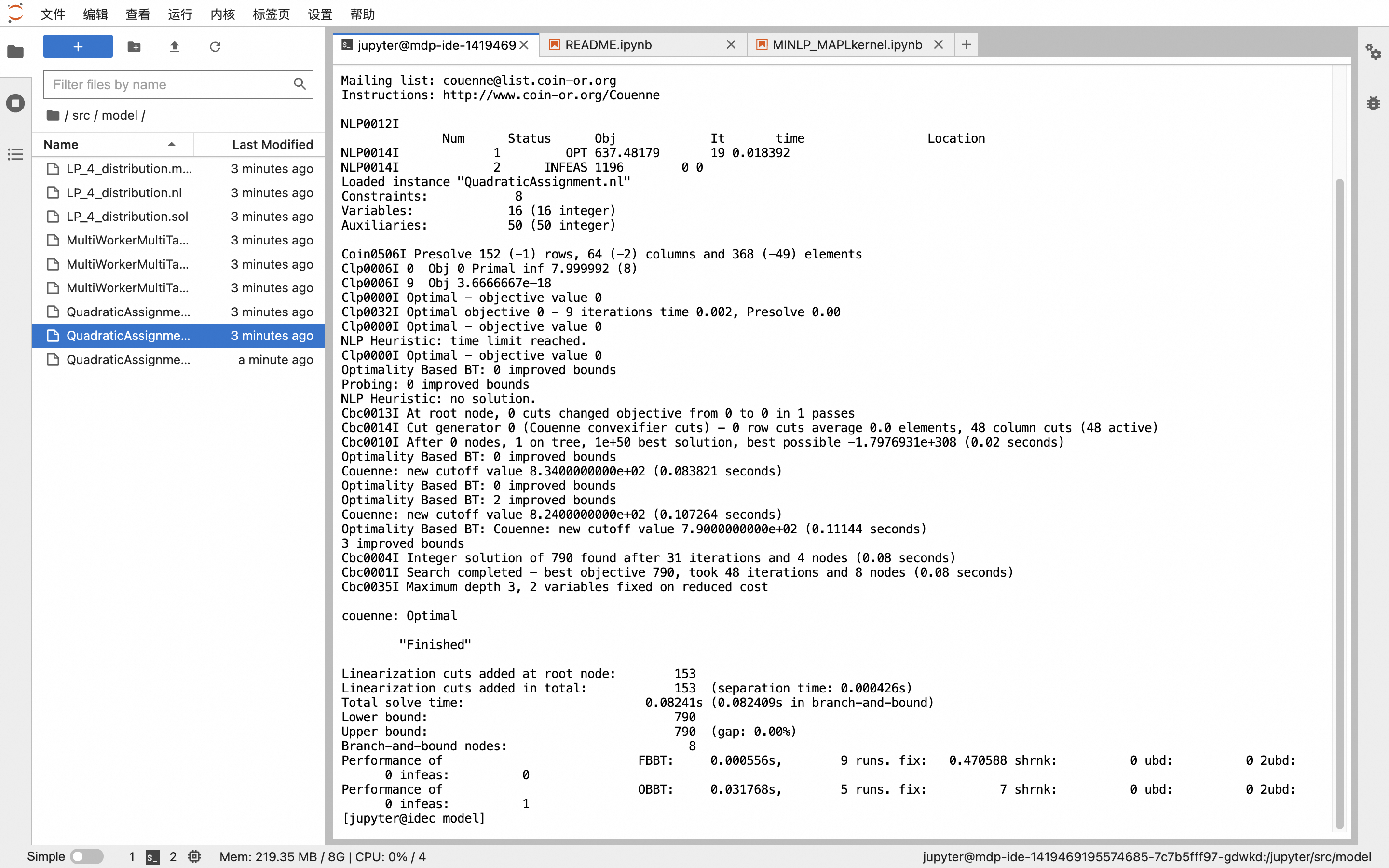
此外,对于建模语言,平台提供了丰富的案例于用户参考学习,例如虚拟电厂智能调度、排产排程等

![[AI编程]AI辅助编程助手-亚马逊AI 编程助手 Amazon CodeWhisperer](https://img-blog.csdnimg.cn/direct/e6d10767d004460c8e79f8604f76bdfc.png)