朋友们,问一个简单的问题:0.1+0.2=?
你肯定会说:中国人不骗中国人,0.1+0.2=0.3。
但是在Python里,0.1+0.2≠0.3 ,我们今天一起来看看这个,并且看一下解决办法。
离奇的错误
在python里编写下列代码,这个代码的含义我就不解释了,我相信即使不懂编程你也能看懂。
编写完成后,运行这个代码,你得到的结果是多少?
a=0.1
b=0.2
c=a+b
print(c) # 在屏幕上,输出这个结果
我运行这个程序的输出结果,如下图所示,👇
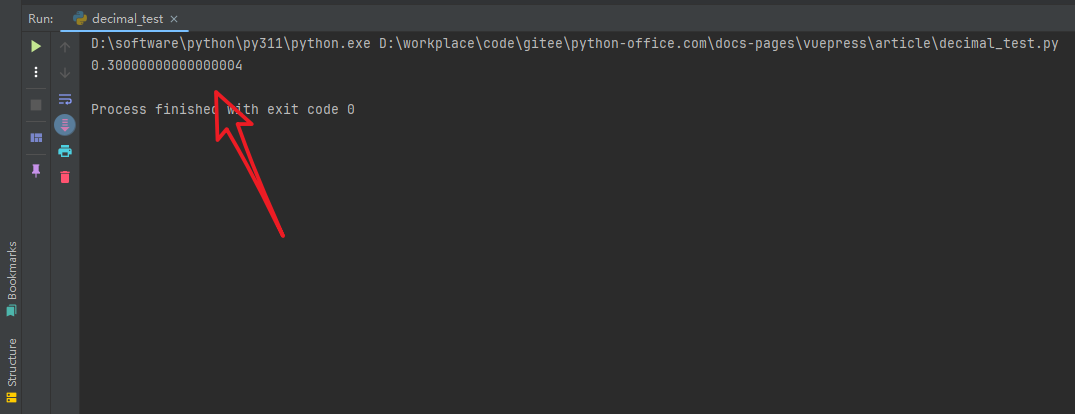
为什么会出现这个结果呢?
这和浮点数在计算机里的表示方法有关,不只是Python有这个问题,其实其它编程语言也这样。
感兴趣的朋友可以点赞本文,点赞满20个,我就专门写一篇文章来解释这一现象的原因。
今天我们先来看一下,出现这种问题,应该如何解决。
有点复杂的解决方法。
这种小数点计算的误差,平时我们可能也察觉不出来,但是这种微小的误差,对于金融类对数字敏感的程序,影响就很大了。
比如我之前写了一个开源项目pofinance,可以通过一行代码计算量化交易中的做T盈亏,如下图所示,👇
# pip install pofinance
import pofinance
good = pofinance.t0(11.2, 11.4, 10000) # 针对10000股,11.2买入,11.4卖出,能赚多少钱?
print(good)
其中t0的函数作用,是进行股票买入卖出的价格计算,经常会涉及到分甚至毫厘的价格计算,必须保证结果100%正确。
我是如何保证结果100%正确的呢?
使用Python里自带的库:decimal和内置函数str,比如上面0.1+0.2的代码,如果想得到正确的结果,代码可以这么写。👇
from decimal import Decimal
a = Decimal(str(0.1)) # 先把0.1转成字符串,再把字符串转成数字
b = Decimal(str(0.2)) # 同上
c = a + b
print(c)
以上代码,运行后的结果,如下图所示,👇
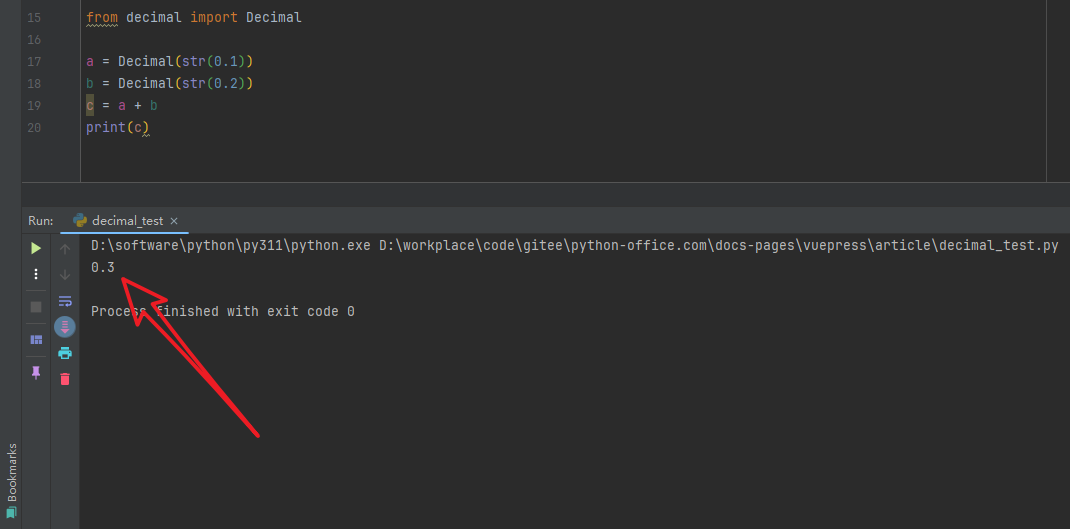
这个解决方法是不是有点复杂,我也觉得太复杂了。
但你还有没有更好的办法呢?欢迎在评论区交流一下~👇



![[Angular] 笔记 11:可观察对象(Observable)](https://img-blog.csdnimg.cn/direct/1ddde1a6f1f747a5bd3a6f1def55ea1d.png)