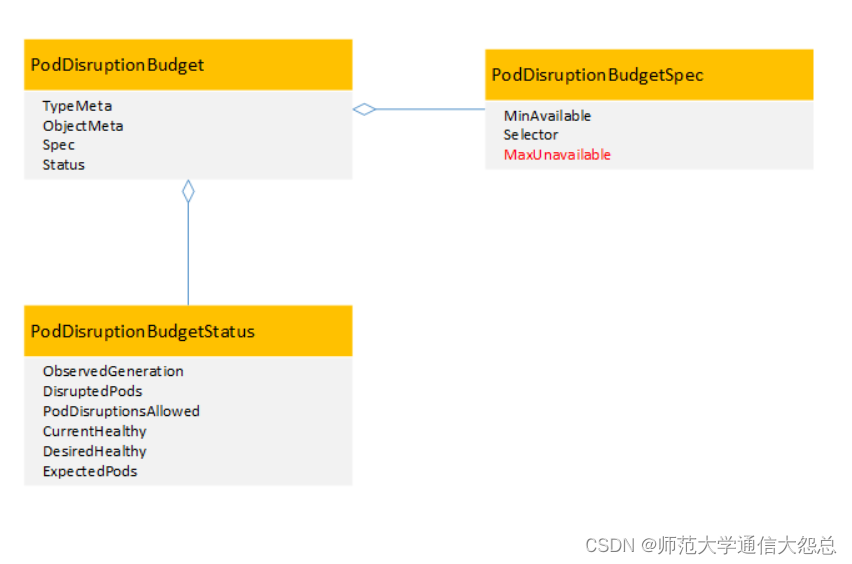
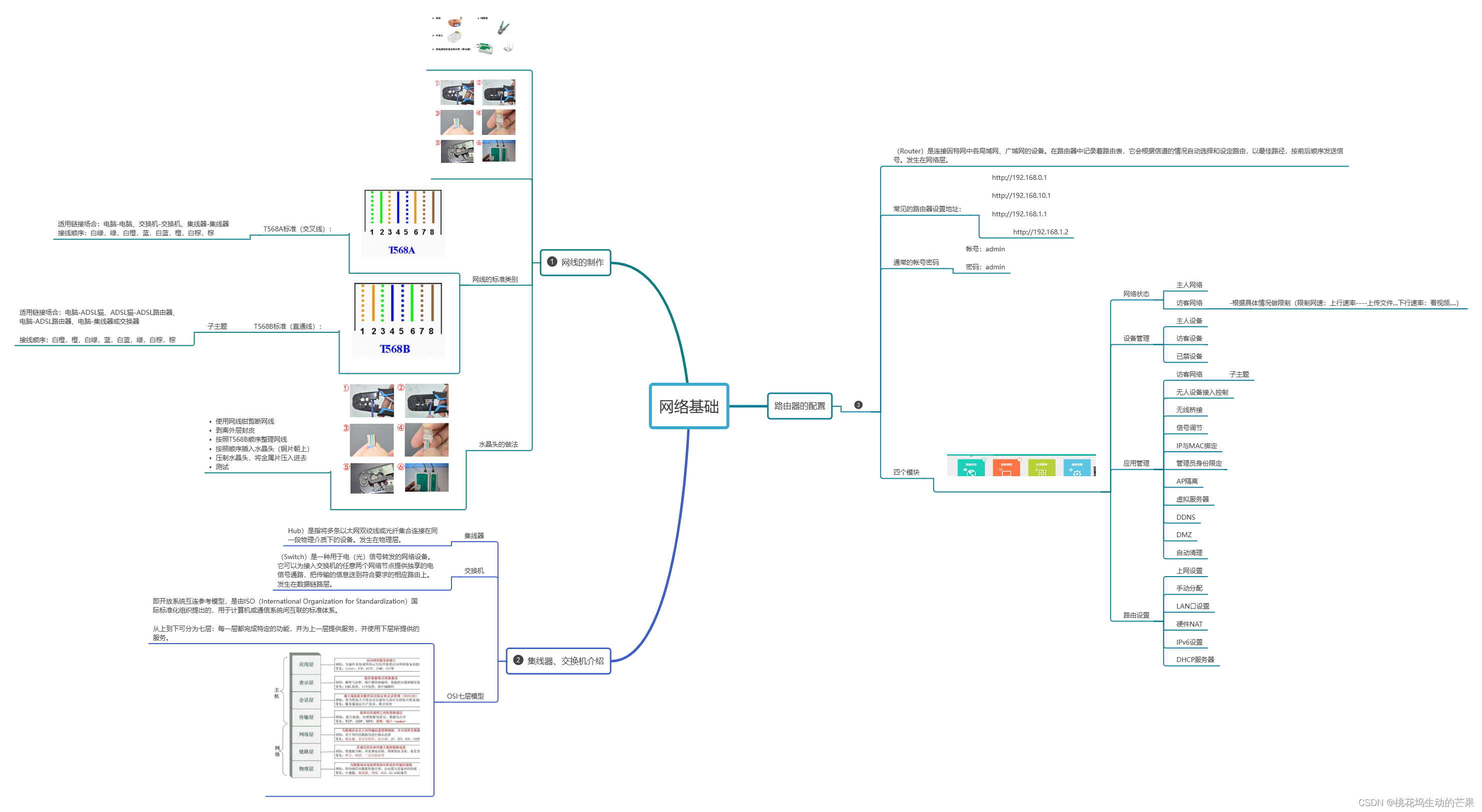
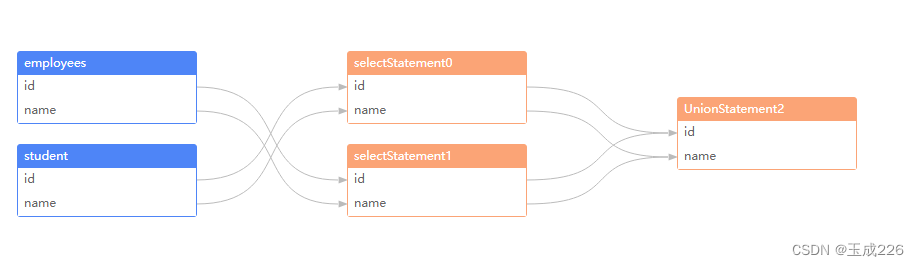
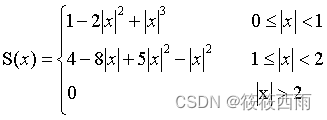针对连续动作空间,策略函数没法预测出每个动作选择的概率。因此使用确定性策略梯度方法。
0 概览
- 1 actor输出确定动作
- 2 模型目标:
actor目标:使critic值最大
critic目标: 使TD error最大 - 3 改进:
使用两个target 网络减少TD error自举估计。
1 actor 和 critic 网络
- 确定性策略网络
actor: a= π ( s ; θ ) \pi(s;\theta) π(s;θ) 输出为确定性的动作a - 动作价值网络
critic Q=q(s,a;w) ,用于评估动作a的好坏
2 critic网络训练
- 观察一组数据
(
s
t
,
a
t
,
r
t
,
s
t
+
1
)
(s_t,a_t,r_t,s_{t+1})
(st,at,rt,st+1)
即在状态 s t s_t st时,执行动作 a t a_t at,得到奖励 r t r_t rt,和下一状态 s t + 1 s_{t+1} st+1 - a t 时刻 Q 值 : q t = q ( s t , a t , w ) a_t时刻Q值: q_t=q(s_t,a_t,w) at时刻Q值:qt=q(st,at,w)
-
a
t
+
1
时刻
Q
值
:
q
t
+
1
=
q
(
s
t
+
1
,
a
t
+
1
,
w
)
a_{t+1}时刻Q值: q_{t+1}=q(s_{t+1},a_{t+1},w)
at+1时刻Q值:qt+1=q(st+1,at+1,w) ,其中
a
t
+
1
=
π
(
s
t
+
1
;
θ
)
a_{t+1}=\pi(s_{t+1};\theta)
at+1=π(st+1;θ)
即TD Target = r t + γ ∗ q t + 1 r_t+\gamma * q_{t+1} rt+γ∗qt+1 - 目标:使t时刻的TD error最小
TD error: δ t = q t − ( r t + γ ∗ q t + 1 ) \delta_t=q_t-(r_t+\gamma * q_{t+1}) δt=qt−(rt+γ∗qt+1)
w = w − α ∗ δ t ∗ ∂ q ( s t , a t ; w ) ∂ w w=w-\alpha *\delta_t* \frac{\partial q(s_t,a_t;w)}{\partial w} w=w−α∗δt∗∂w∂q(st,at;w)
3 actor 网络训练
actor 网络目标是时critic值最大,所以要借助critic网络,将actor值带入critic网络,使critic最大。
- a=
π
(
s
;
θ
)
\pi(s;\theta)
π(s;θ) ,带入q(s,a;w)中 得到 q(s,
π
(
s
;
θ
)
\pi(s;\theta)
π(s;θ) ;w)
即使 q(s, π ( s ; θ ) \pi(s;\theta) π(s;θ) ;w) 最大
对 θ \theta θ求导:
g = ∂ q ( s , π ( s ; θ ) ; w ) ∂ θ = ∂ a ∂ θ ∗ ∂ q ( s , a ; w ) ∂ a g=\frac{\partial q(s,\pi(s;\theta);w)}{\partial \theta}=\frac{\partial a }{\partial \theta} *\frac{\partial q(s,a;w) }{\partial a} g=∂θ∂q(s,π(s;θ);w)=∂θ∂a∗∂a∂q(s,a;w) - 参数更新
θ = θ + β ∗ g \theta=\theta + \beta* g θ=θ+β∗g
4 训练改进
4.1 主网络actor和critic更新
critic 网络更新时,在计算TD error时,使用了自举,会导致数据过高估计或者过低估计。
关键在于
t
+
1
t+1
t+1时刻的
a
t
+
1
和
q
t
+
1
怎么生成
a_{t+1}和q_{t+1}怎么生成
at+1和qt+1怎么生成
和其他方法一样,可以使用两个actor和两个critic网络,减少自举带来的估计。
- t+1 时的
a
t
+
1
a_{t+1}
at+1使用另一个target 策略网络actor生成
a t + 1 = π ( s t + 1 ; θ ˉ ) a_{t+1}=\pi(s_{t+1};\bar\theta) at+1=π(st+1;θˉ) - 同样t+1时
q
t
+
1
q_{t+1}
qt+1使用另一个target critic网络生成
q t + 1 = q ( s t + 1 , a t + 1 ; w ˉ ) q_{t+1}=q(s_{t+1},a_{t+1};\bar w) qt+1=q(st+1,at+1;wˉ)
actor 参数更新方式不变。
critic更新方式变化,使用了target网络产生的
a
t
+
1
和
q
t
+
1
a_{t+1}和q_{t+1}
at+1和qt+1

4.2 target网络actor和critic更新
target 网络初始时来自主网络,后期更新时,部分来自主网络,部分来自自己。
w
ˉ
=
τ
∗
w
+
(
1
−
τ
)
∗
w
ˉ
\bar w= \tau *w +(1-\tau) * \bar w
wˉ=τ∗w+(1−τ)∗wˉ
θ
ˉ
=
τ
∗
θ
+
(
1
−
τ
)
∗
θ
ˉ
\bar \theta= \tau *\theta +(1-\tau) * \bar \theta
θˉ=τ∗θ+(1−τ)∗θˉ
5 其他改进措施
- 添加经验回放, Experience replay buffer
- 多步TD target
- target networks