01背包详解，状态设计，滚动数组优化，通用问题求解

文章目录

0/1背包
- 前言
- 一、0/1背包的状态设计
- - 1、状态设计
  - 2、状态转移方程
  - 3、初始状态
  - 4、代码实现
  - 5、滚动数组优化
  - - 二维优化为两个一维
    - 二维优化为一个一维，倒序递推
- 二、0/1背包的通用问题
- - 求最大值
  - 求最小值
  - 求方案数

0/1背包

前言

0/1包问题，作为动态规划问题的经典问题，可以帮助捋顺思维。核心就是有一堆物品,有两个维度的限制，在保证一个维度限制的情况下，使得另一个维度最优。

一、0/1背包的状态设计

有n(n≤100)个物品和一个容量为m(m≤10000)的背包。
第i个物品的容量是c[i]，价值是w[i]。现在需要选择一些物品放入包, 总容不能超过背包容量，求能够达到的物品的最大总价值。

以上就是0/1背包问题的完整描述,之所以叫0/1背包，因为每种物品只有一个,可以选择
放入背包或者不放，而0代表不放，1 代表放。

1、状态设计

状态(i, j)表示前i个物品恰好放入容量为j的背包(0≤i<n，0≤j≤m);
令dp表[][]示状态(i, j)下该背包得到的最大价值，即前i个物品恰好放入容量为j的背包所得
到的最大总价值;

2、状态转移方程

列出状态转移方程如下:
$d p [i] [j] = ma x (d p [i - 1] [j], d p [i - 1] [j - c [i]] + w [i])$
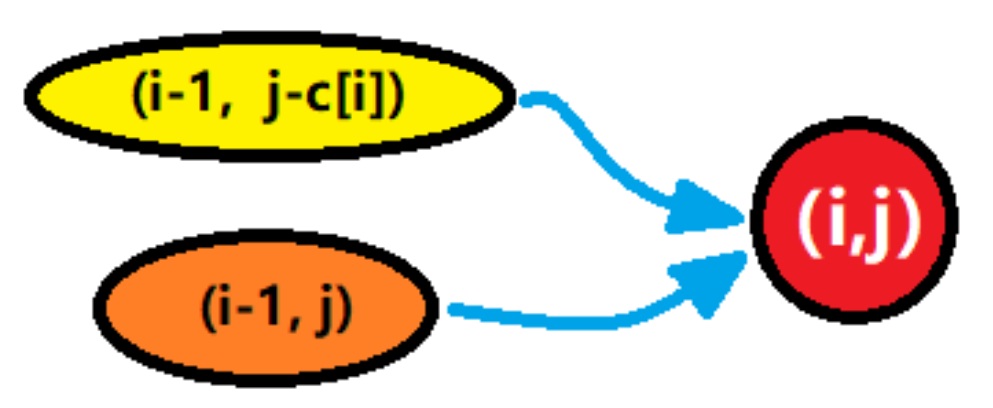
因为每个物品要么放,要么不放,所以只需要考虑第i个物品放或不放的情况:

1)不放:如果第i个物品不放入容量为j的背包",那么问题转化成求"前i-1 个物品放入容为j的背包"的问题;于不放,所以最大价值就等于"前i-1个物品放入容量为j的背包"的最大价值，即dp[i-1][j];

2)放:如果"第i个物品放入容为j的背包"，那么问题转化成求"前i-1个物品放入容量为j-c[j]的背包"的问题;那么此时最大价值就等于"前i-1个物品放入容为j-c[i] 的背包"的最大价值加上放入第i个物品的价值,即dp[i-1][j - c[i]] + w[i]
将以上两种情况取大者,就是我们所求的“前i个物品恰好放入容量为j的背包"的最大价值了。

在这里插入图片描述

3、初始状态

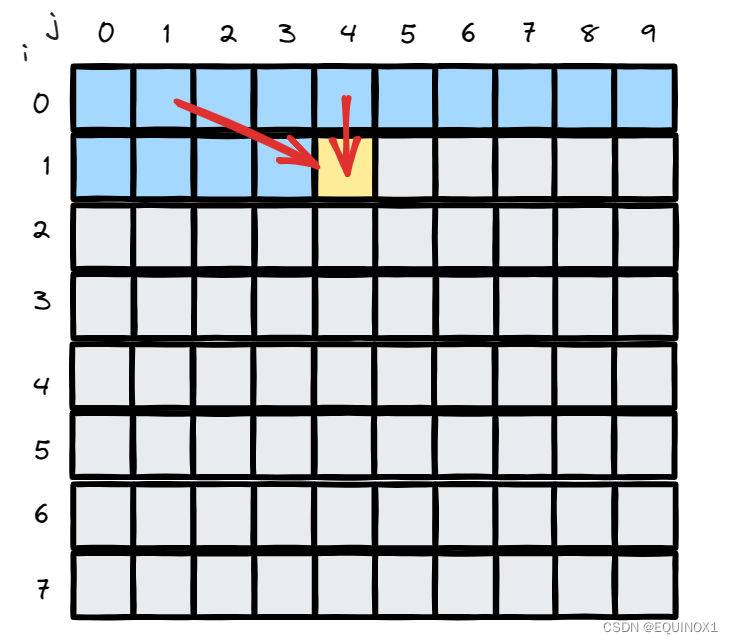
我们发现，当状态在进行转移的时候，dp(i, j)不是来自dp(i - 1 , j),就是来自dp(i - 1 , j - c[i])，所以必然有一个初始状态，而这个初始状态就是(0, i)，含义是"前i个物品放入一个容量为0的背包"，这个状态下的最大价值为0,即dp[0][i] = 0;

4、代码实现

铺垫了那么多，我们来实现一下0/1背包的板子。

//#define N 110
//#define M 1010
//int dp[N][M]{0}, c[N]{0}, w[N]{0}, n, m;
//c[i]为第i个物品的重量，w[i]为第i个物品的价值。n、m分别为物品数和背包容量
for (int i = 1; i <= n; i++)
    for (int j = 0; j <= m; j++)
        if (j < c[i])
            dp[i][j] = dp[i - 1][j];
        else
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i]);

5、滚动数组优化

滚动数组优化为递推问题中的常用空间优化手段，如果每次递推都由上一次状态转移那么我们可以将空间降低一个维度。

我们再看状态转移图

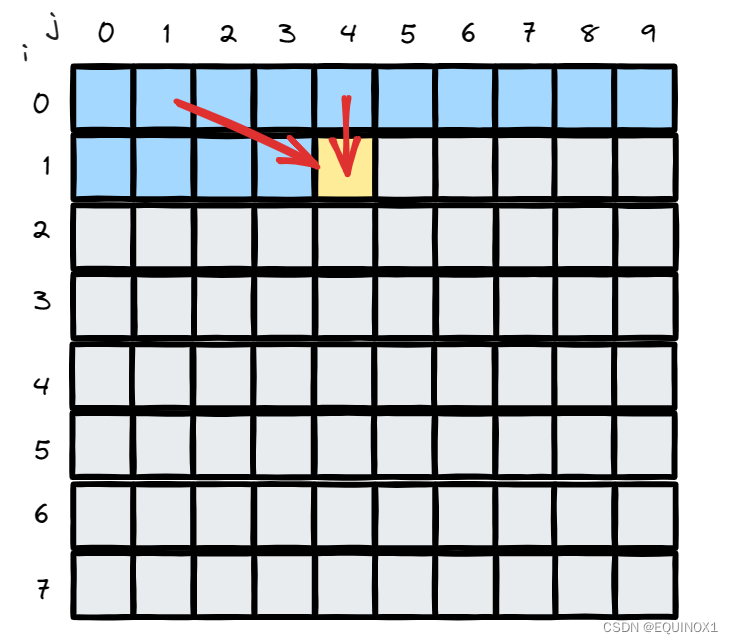
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

发现每个状态都只跟上一行同一列和上一行左边的状态有关，我们可以开两个一维数组，分别保存上一行和当前行的状态，当然也可以只用一个一维数组然后倒序递推来实现。

二维优化为两个一维

两个一维数组一个保存上一行的状态一个保存当前行状态即可。

#define N 110
#define M 1010
int dp1[M]{0}, dp2[M]{0}, c[N]{0}, w[N]{0}, n, m;
for (int i = 1; i <= n; i++)
    cin >> c[i] >> w[i];
for (int i = 1; i <= n; i++)
{
    for (int j = 0; j <= m; j++)
        if (j < c[i])
            dp2[j] = dp1[j];
        else
            dp2[j] = max(dp1[j], dp1[j - c[i]] + w[i]);
    memcpy(dp1, dp2, sizeof(dp1));
}
cout << dp2[m];

二维优化为一个一维，倒序递推

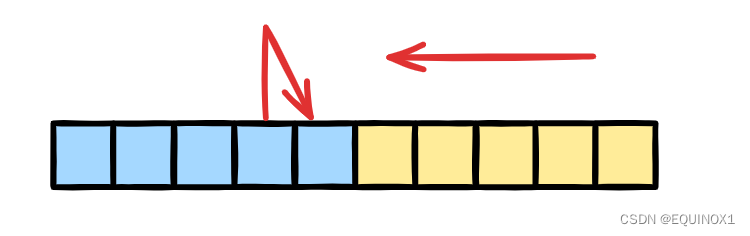
即然每次状态都只由上一行当前列和当前行左侧列转移，我们发现两个一维优化方案中，dp1其实是也可以优化掉的，假如只剩下一个一维数组dp，如果我们正序递推会怎样？

初始时dp中存储上一次状态转移的数据，如果正序递推则导致我们状态转移需要上一次状态但是由于正序递推覆盖了左侧内容，就无法获取上一次状态了，所以我们选择逆序递推：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

#define N 110
#define M 1010
int dp[M]{0}, dp2[M]{0}, c[N]{0}, w[N]{0}, n, m;
for (int i = 1; i <= n; i++)
    cin >> c[i] >> w[i];
for (int i = 1; i <= n; i++)
{
    for (int j = m; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
}
cout << dp[m];

二、0/1背包的通用问题

求最大值

原题链接

[P1048 NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

01背包板子题，读完数据跑一遍板子，输出数据即可。

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 110
#define M 1010
int dp[M]{0}, c[N]{0}, w[N]{0}, n, m;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> m >> n;
    for (int i = 1; i <= n; i++)
        cin >> c[i] >> w[i];
    for (int i = 1; i <= n; i++)
    {
        for (int j = m; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    }
    cout << dp[m];
    return 0;
}

[P1060 NOIP2006 普及组] 开心的金明 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

同样是01板子题，只不过物品价值变成了重量乘价值

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 30010
#define M 100000000
int dp[M]{0}, c[N]{0}, w[N]{0}, n, m;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> m >> n;
    for (int i = 1; i <= n; i++)
        cin >> c[i] >> w[i], w[i] *= c[i];

    for (int i = 1; i <= n; i++)
    {
        for (int j = m; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    }
    cout << dp[m];
    return 0;
}

P3985 不开心的金明 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

在不考虑内存的情况下显然是一道01背包板子题，但是你这个1e9的背包内存肯定会爆，内存不爆你时间复杂度也会爆，但是金明妈妈限制了物品重量极差不超过3（感谢金明妈妈！！！！），我们就可以将物品重量离散化到1，2，3，4上，即我们记录最小重量mi，再令每个重量减去(mi - 1)，这样物品重量就变为了1，2，3，4

由于物品数目最多100，所以物品总重量最大也就400，我们离散化后再去跑01背包的板子即可

但是！！！

有一个问题，你怎么根据离散化后的重量计算离散化前的重量呢？看我们的板子

for (int i = 1; i <= n; i++)
{
    for (int j = sum; j >= c[i]; j--)
        dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
}

此时j为离散化后的重量了，你怎么确定你上面的状态方程就合法呢？如果一共给了m的空间，你此时的j对应实际重量为j + cnt * mi，cnt为装的物品数目，故而我们需要给dp增加一个维度来记录装入的物品数目

dp[i][j]就代表容量i装入了j个物品的最大价值，此时装入总重量不超过i + j * mi，（不超过是因为i可能大于j个物品的离散重量）

这样一来我们的空间复杂度只有1e2量级，时间复杂度只有1e6量级

代码如下：

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 110
#define M 550
int dp[M][N]{0}, c[N]{0}, w[N]{0}, n, m, mi = INT_MAX, sum = 0, ans = 0;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> c[i] >> w[i], mi = min(mi, c[i]);
    mi--;
    for (int i = 1; i <= n; i++)
        c[i] -= mi, sum += c[i];

    for (int i = 1; i <= n; i++)
    {
        for (int j = sum; j >= c[i]; j--)
            for (int k = (m - j) / mi ; k >= 1; k--)
                ans = max(ans, dp[j][k] = max(dp[j][k], dp[j - c[i]][k - 1] + w[i]));
    }
    cout << ans;
    return 0;
}

求最小值

原题链接

[P1049 NOIP2001 普及组] 装箱问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

本质还是求最大值。

在本题内，重量就是体积，价值也是体积，我们求出能装的最大体积，容量减去最大体积就是答案。

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 50
#define M 20010
int dp[M]{0}, c[N]{0}, w[N]{0}, n, m;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> m >> n;
    for (int i = 1; i <= n; i++)
        cin >> c[i];
    for (int i = 1; i <= n; i++)
    {
        for (int j = m; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + c[i]);
    }
    cout << m - dp[m];
    return 0;
}

求方案数

原题链接

P1164 小A点菜 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

对于本道题我们的dp[i][j]就变成了j元恰好买i道菜的方案数

对于初始状态即0元购0菜方案为1，其他0元购都是0

那么我们同样对于每道菜可以选择买或不买，可以选择用j元恰好买i - 1道菜也可以选择用j元恰好买i道菜，那么转移方程就变成了

dp[i][j] = dp[i - 1][j] + dp[i - 1][j - c[i]]

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 110
#define M 10010
int dp[M]{0}, c[N]{0}, w[N]{0}, n, m;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> c[i];
    dp[0] = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = m; j >= c[i]; j--)
            dp[j] += dp[j - c[i]];
    }
    cout << dp[m];
    return 0;
}