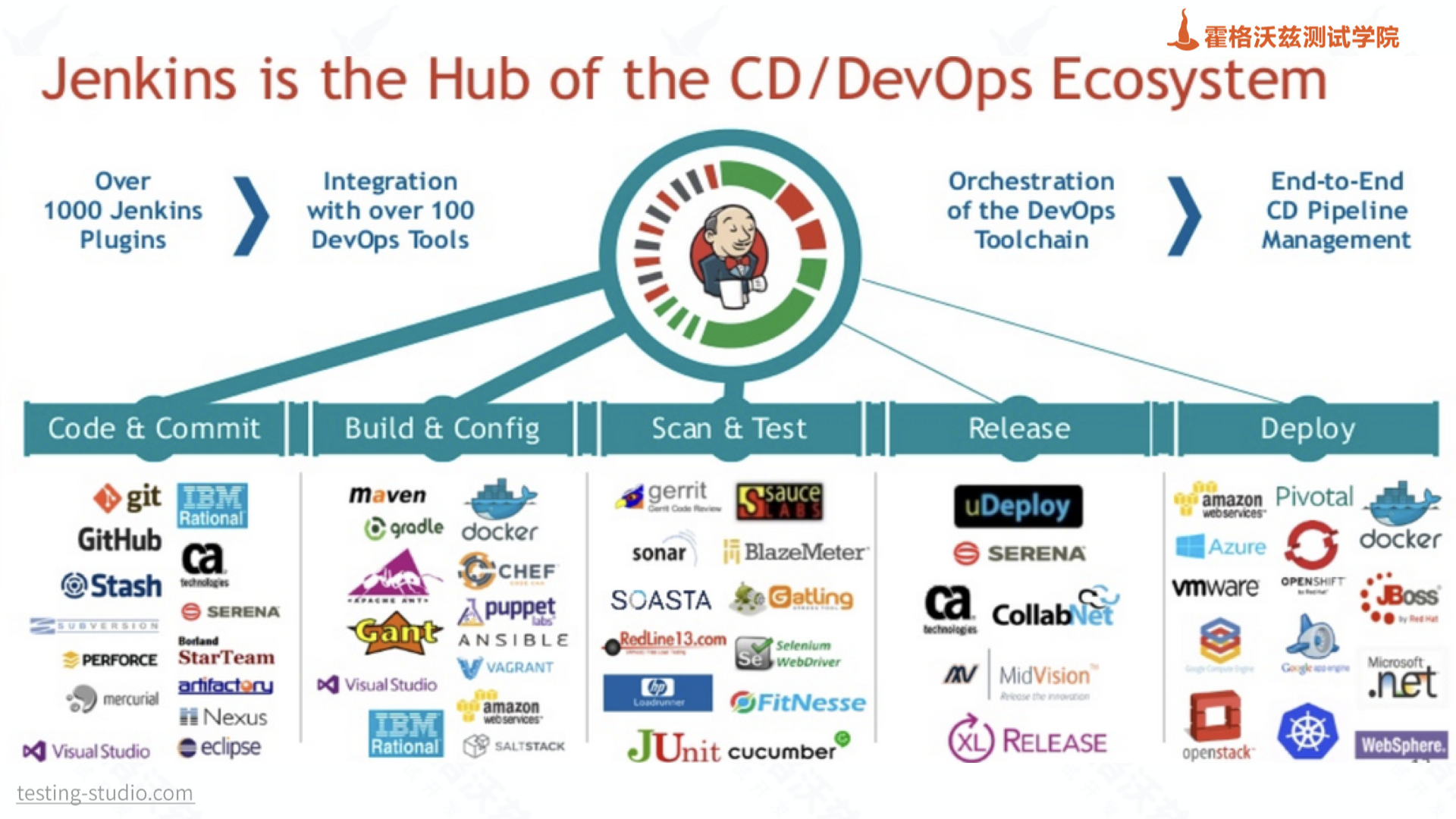
INS 会受到误差的扰动， INS 的误差方程进行推导。常用的误差模型有 PHI 角和 PSI 角误差
模型。PHI 角误差模型是基于平台坐标系与真实导航坐标系推导的，误差模型易于理解但形式较为复杂。PSI 角误差模型是基于平台坐标系和计算坐标系推导的，误差模型形式简单。

1、姿态微分方程

余弦矩阵微分

固定矢量r 在两坐标系 i 和b 下投影的转换关系，即坐标变换为

 方程左边r是固定的，所以求微分后为0，右边方程第一项：b系相对于i系的角速率wib, 上标是基准，那么rb的微分就是b系下看r的角速率是负wib，rb的微分就是-wib x rb；

所以微分方程就整理成

所以

在组合导航中，n系作为参考系，b是载体系

式中的角度是未知的，需要拆解，变换得到，

        将 角度拆解后代入上式的微分方程 ，

上面的红线用到了下面的公式

所以

四元数微分

改写

方向余弦、四元数更新算法式 两种算法都是假设在更新周期内动坐标系作定轴转动时才能严格成立的，如果不是定轴转动，由角增量直接求解变化矩阵或四元数，会引入转动不可交换误差。

2、速度微分方程

速度微分方程  加计在导航系下的加速度 不代表载体的运动状态，需要扣除有害加速度后得到的才是载体的加速度。

3、位置微方程