信号与线性系统翻转课堂笔记8—

信号与线性系统翻转课堂笔记8——周期信号的频谱

news2025/4/19 10:14:15

信号与线性系统翻转课堂笔记8——周期性信号的频谱

The Flipped Classroom8 of Signals and Linear Systems

对应教材：《信号与线性系统分析（第五版）》高等教育出版社，吴大正著

一、要点

（1，重点）周期信号频谱的概念及其物理意义；
（2，重点）周期矩形脉冲频谱的形状和特点，了解取样函数及其特点，掌握周期和脉冲宽度变化对周期矩形脉冲频谱的影响；
（3）频带宽度的概念及其在工程实际中的意义。

二、问题与解答

1、取样函数（也称为样本函数）是本课程中另外一个非常重要的信号。在MATLAB中，定义了一个sinc函数来表示取样函数，但是sinc函数的定义方式与教材对取样函数的定义方式略有区别。①请查阅资料以及MATLAB帮助文件，找出这两者定义的差别，并说明如果用sinc函数来求取样函数，应该怎么处理；②基于sinc函数，画出取样函数波形，并总结该函数波形的特点。
2、针对偶对称的周期矩形脉冲（教材图4.3-2），其中T和τ的值自定，利用MATLAB分别画出其单边和双边频谱（幅度谱和相位谱合二为一），单边谱的公式参见课件。①总结单边谱与双边谱的区别与联系，说明已知单边谱，如何画出双边谱；②如何理解双边谱中负频率的物理意义？③如果周期矩形脉冲左移或者右移（使得其不再偶对称），则分别会对其幅度频谱和相位频谱产生何种影响？此时能不能仍然采用幅度谱相位谱合二为一的方式绘制频谱图？
在这里插入图片描述

3、上一题中，改变周期矩形脉冲T和τ及其比值T/τ，会对频谱波形产生何种影响，利用MATLAB绘图举例进行分析，根据频谱的物理意义对所得结果进行解释（为什么会增大/减小信号中的高频/低频分量），并据此总结周期矩形脉冲时域脉宽与频谱带宽之间的关系、时域脉冲密度与频谱谱线密度之间的关系。
4、周期矩形脉冲信号的频带宽度是如何定义的？这种定义方式是否适用于任意的周期信号？脉冲宽度的变化对于周期矩形脉冲信号带宽有什么影响？这种影响对于分析和研究信号传输技术具有何种意义（信息是要依靠信号的变化来传输的，变化越快的信号，可以包含越大的信息量，从这个角度进行分析）？
5、
在这里插入图片描述
6、
傅里叶级数帕斯瓦尔恒等式的物理意义是什么？周期矩形脉冲信号频谱带宽范围内是否包含了全部的信号功率？

1、取样函数&sinc函数

取样函数（也称为样本函数）是本课程中另外一个非常重要的信号。在MATLAB中，定义了一个sinc函数来表示取样函数，但是sinc函数的定义方式与教材对取样函数的定义方式略有区别。①请查阅资料以及MATLAB帮助文件，找出这两者定义的差别，并说明如果用sinc函数来求取样函数，应该怎么处理；②基于sinc函数，画出取样函数波形，并总结该函数波形的特点。

区别：
1、sinc函数是正孩基函数的缩写，sinc(X)=sin(pix)/(pix)
2、Sa函数是采样函数的缩写，Sa（X）=sin（X）/X
sinc函数和Sa函数之间相互转换：sinc(X)=Sa(pi*x)。

t=-3*pi:pi/100:3*pi;
ft=sinc(t/pi);
plot (t,ft);
grid on;

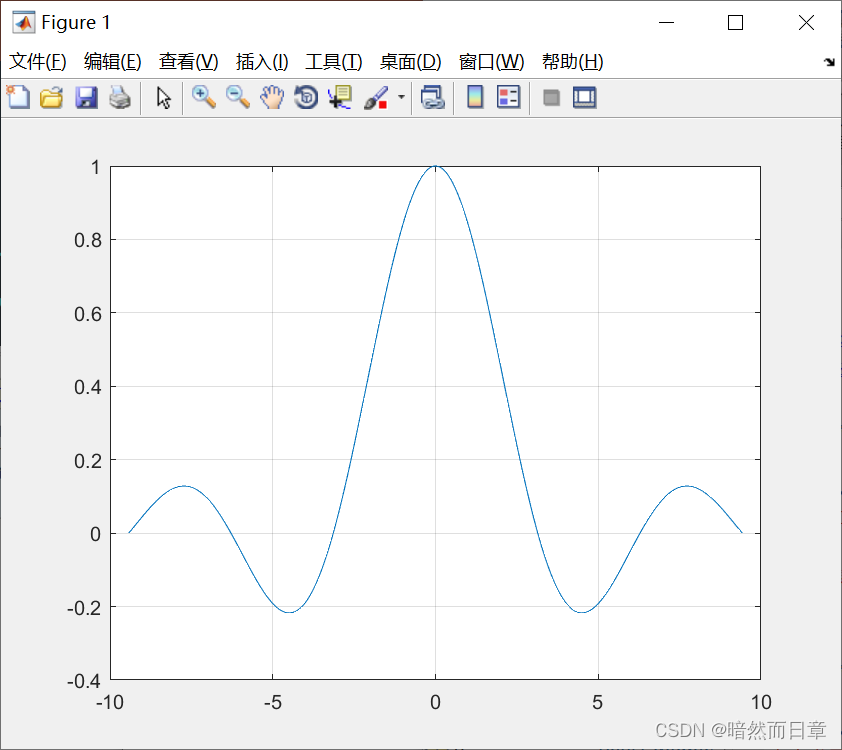
在这里插入图片描述
特点：这是一个偶函数图像，自变量为0时采样函数的值是1，在自变量取pi的非零整数倍时为0，抽样函数在自变量趋近于无穷时函数值趋近于0。

2、单边谱和双边谱

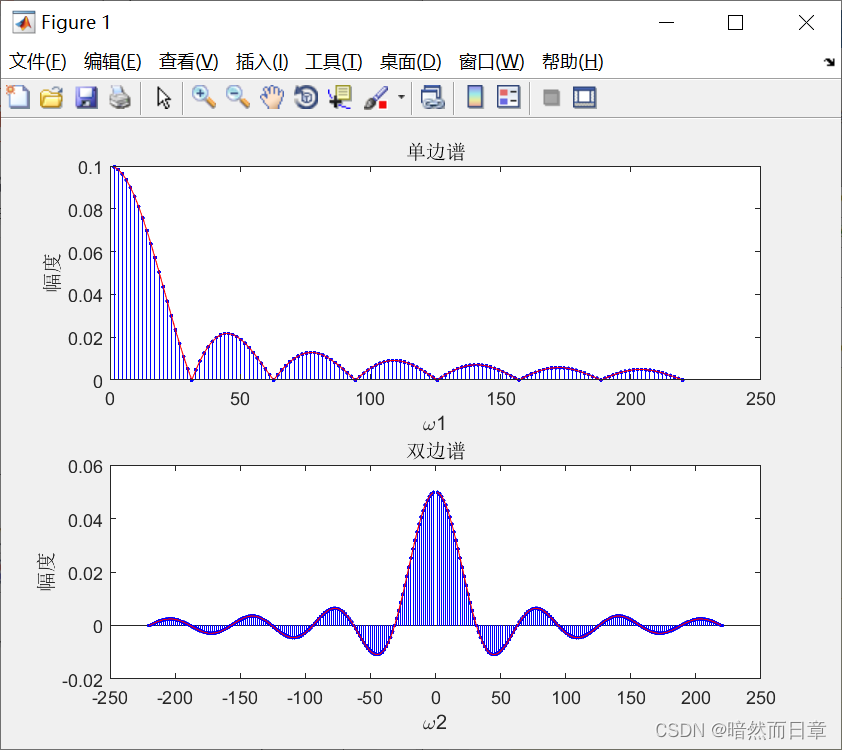
针对偶对称的周期矩形脉冲（教材图4.3-2），其中T和τ的值自定，利用MATLAB分别画出其单边和双边频谱（幅度谱和相位谱合二为一），单边谱的公式参见课件。①总结单边谱与双边谱的区别与联系，说明已知单边谱，如何画出双边谱；②如何理解双边谱中负频率的物理意义？③如果周期矩形脉冲左移或者右移（使得其不再偶对称），则分别会对其幅度频谱和相位频谱产生何种影响？此时能不能仍然采用幅度谱相位谱合二为一的方式绘制频谱图？
在这里插入图片描述

T=2;            %周期矩形脉冲周期为T
tao=1/5;        %脉宽为tao
E=1;            %脉冲高度为E
omega=2*pi/T;   %Ω=2π/T

omega1=0:omega:70*pi;
a=(2*E*tao/T).*sin(omega1*tao/2)./(omega1*tao/2);   %公式1见PPT
fudu1=abs(a);

omega2=-70*pi:omega:70*pi;
fudu2=(E*tao/T).*sin(omega2*tao/2)./(omega2*tao/2); %公式2见PPT

subplot(2,1,1)      %画图                  
stem(omega1,fudu1,'b.');
hold on
plot(omega1,fudu1,'r-');
hold off
xlabel('\omega1');
ylabel('幅度');
title('单边谱');
subplot(2,1,2)
stem(omega2,fudu2,'b.');
hold on
plot(omega2,fudu2,'r-');
hold off
xlabel('\omega2');
ylabel('幅度');
title('双边谱');

蓝色部分为公式1：
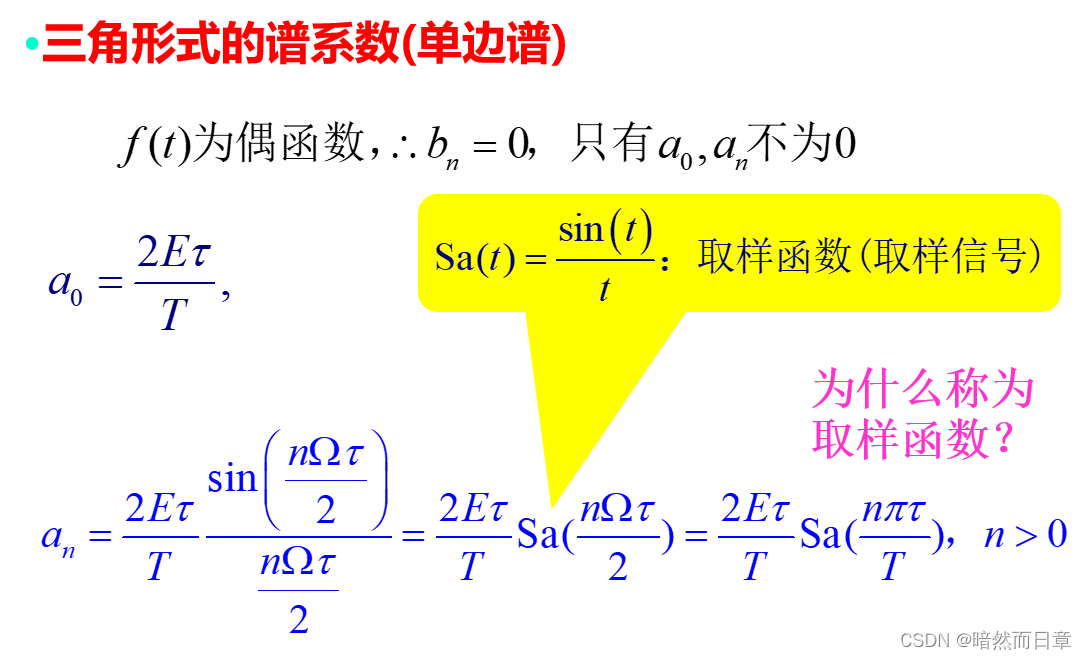
在这里插入图片描述
蓝色部分为公式2：

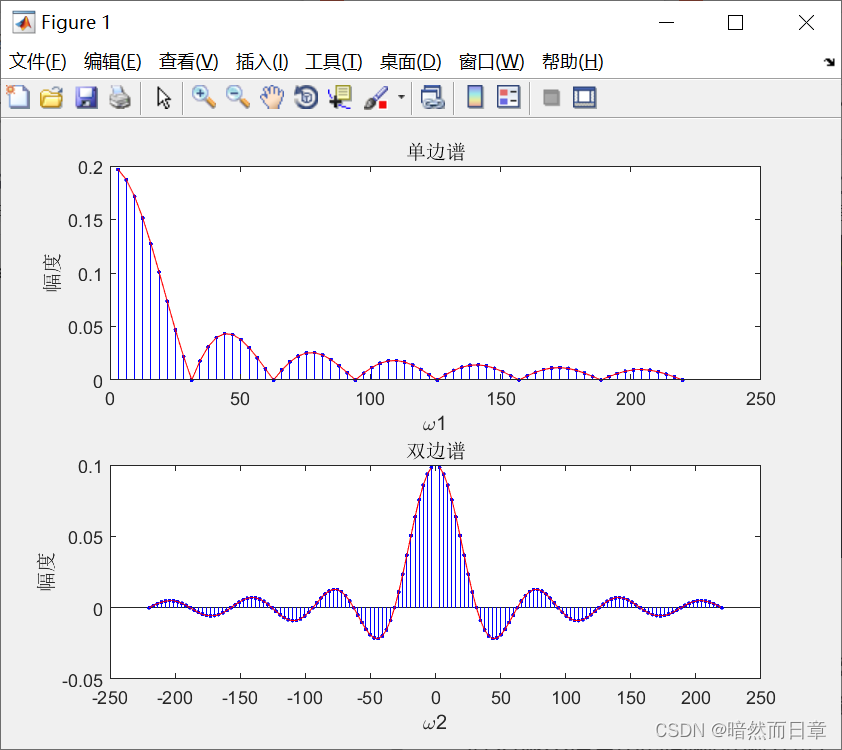
在这里插入图片描述
（1）
区别：
双边谱负频率只有数学意义没有物理意义；
双边谱为偶函数，单边谱非奇非偶；
双边谱幅度除了w=0时，是单边谱的二分之一。
联系：
频谱带宽相同；
谱线密度相同；
频谱都具有离散性、谐波性和收敛性。
已知单边谱，可将其幅度除了w=0时，其余缩小一半，并作其关于y轴的对称。
（2）
双边谱负频率只有数学意义没有物理意义，负频率的存在使得构成实信号。
（3）
平移后，脉冲不为偶对称波形，会产生正弦分量，Fn从实数变为复数，幅度谱不变，相位谱变化。因此，不能采用幅度谱相位谱二合一的方式绘制频谱图。

3、脉宽和脉冲密度对频谱的影响

上一题中，改变周期矩形脉冲T和τ及其比值T/τ，会对频谱波形产生何种影响，利用MATLAB绘图举例进行分析，根据频谱的物理意义对所得结果进行解释（为什么会增大/减小信号中的高频/低频分量），并据此总结周期矩形脉冲时域脉宽与频谱带宽之间的关系、时域脉冲密度与频谱谱线密度之间的关系。

T=2，tao=1/5，T/tao=10

在这里插入图片描述

T=2，tao=1/10，T/tao=20
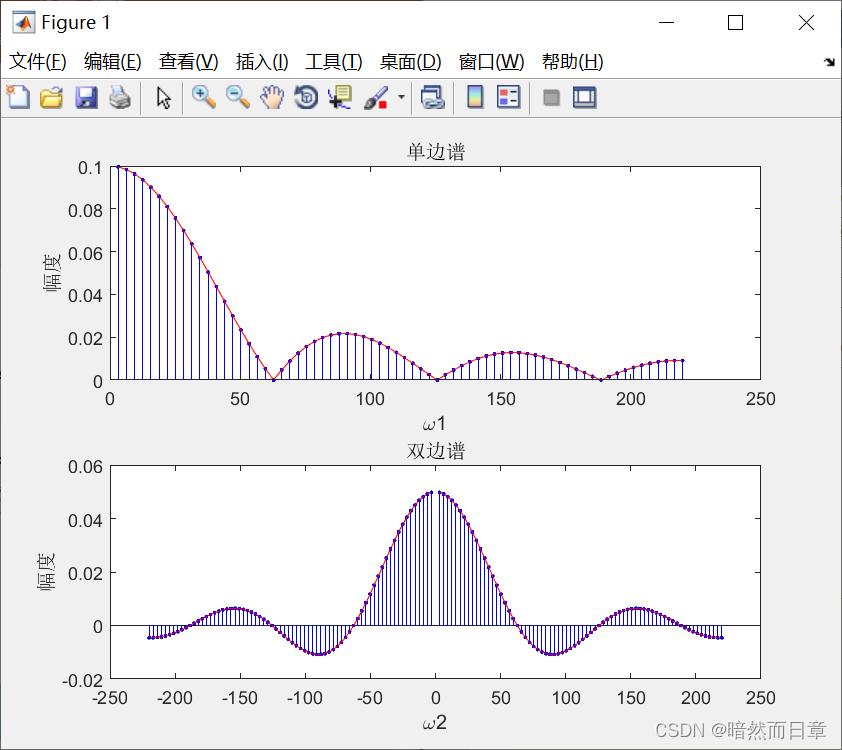
在这里插入图片描述
T=4，tao=1/5，T/tao=20

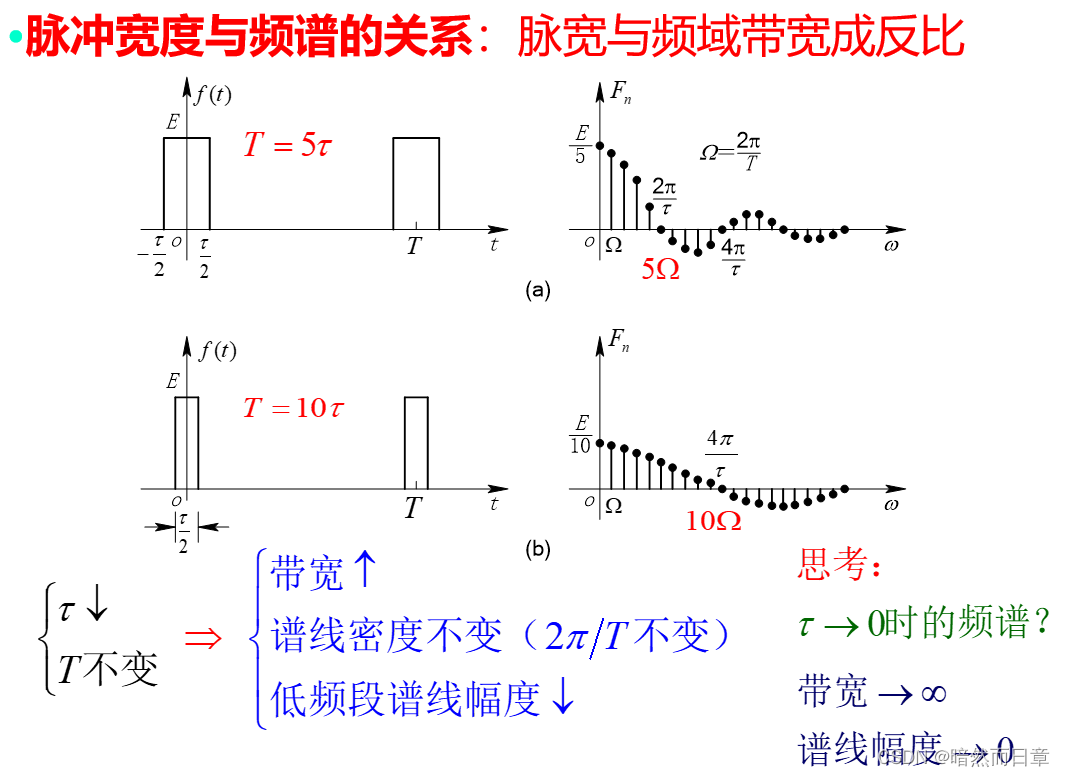
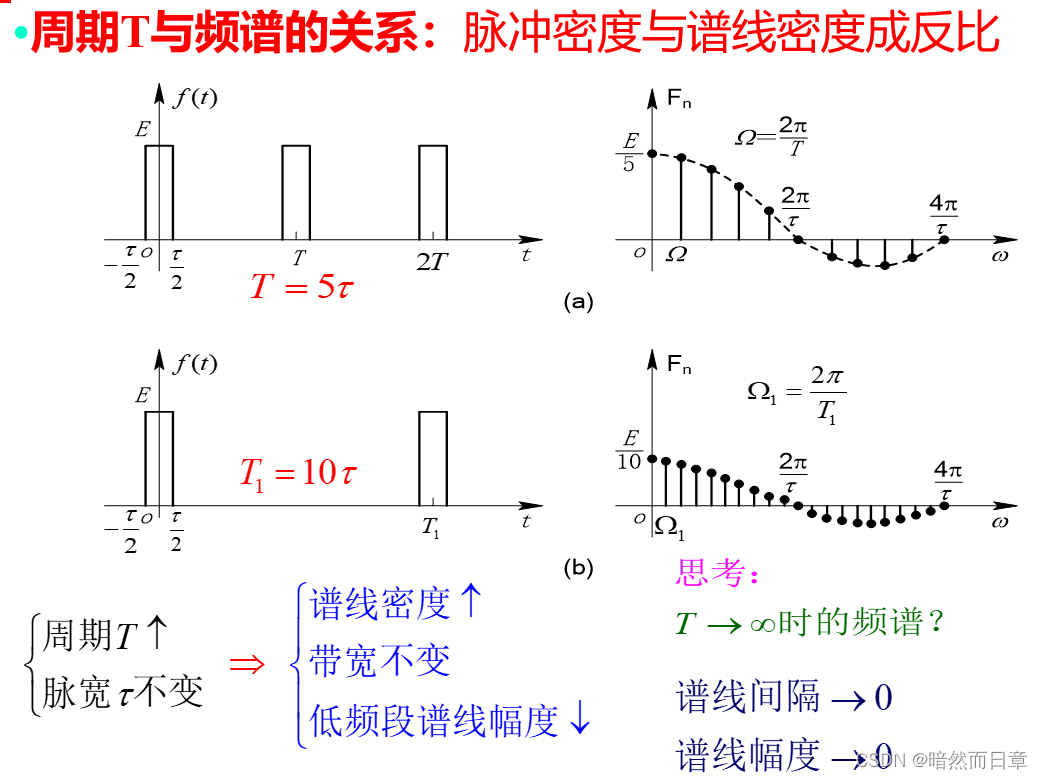
在这里插入图片描述

4、脉冲宽度和频带宽度

周期矩形脉冲信号的频带宽度是如何定义的？（第一问）这种定义方式是否适用于任意的周期信号？（第二问）脉冲宽度的变化对于周期矩形脉冲信号带宽有什么影响？（第三问）这种影响对于分析和研究信号传输技术具有何种意义（信息是要依靠信号的变化来传输的，变化越快的信号，可以包含越大的信息量，从这个角度进行分析）？（第四问）

在这里插入图片描述

5、周期单位冲激序列频谱

在这里插入图片描述

周期单位冲激序列：
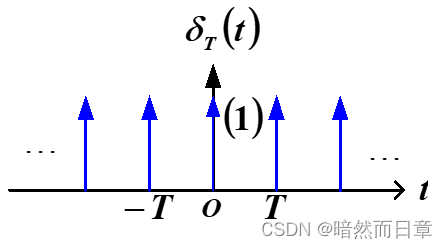
在这里插入图片描述
频谱：

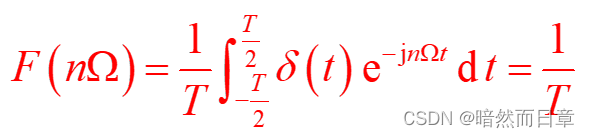
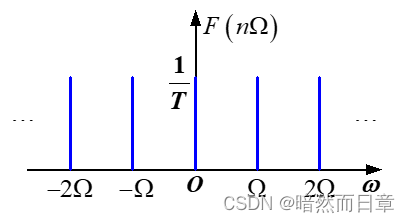
在这里插入图片描述

6、傅里叶级数帕斯瓦尔恒等式

傅里叶级数帕斯瓦尔恒等式的物理意义是什么？周期矩形脉冲信号频谱带宽范围内是否包含了全部的信号功率？

在这里插入图片描述
在区间(t1,t2),信号f（t）所含有的能量恒等于此信号在完备正交集中各正交分量能量之和。即周期信号平均功率=直流、基波及各次谐波分量有效值的平方和。说明时域和频谱能量守恒。这是帕斯瓦尔定理在傅里叶级数条件下的体现。
周期矩形脉冲信号频谱带宽范围内包含了绝大部分信号功率，但是没有包含全部的信号功率。