Pooling方法总结（语音识别）

news2025/2/5 7:48:56

Pooling layer将变长的frame-level features转换为一个定长的向量。

1. Statistics Pooling

链接：http://danielpovey.com/files/2017_interspeech_embeddings.pdf

The default pooling method for x-vector is statistics pooling.

The statistics pooling layer calculates the mean vector µ as well as the second-order statistics as the standard deviation vector σ over frame-level features ht (t = 1, · · · , T ).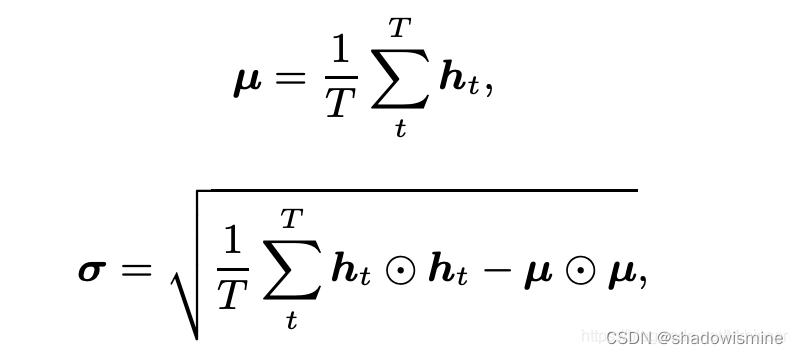

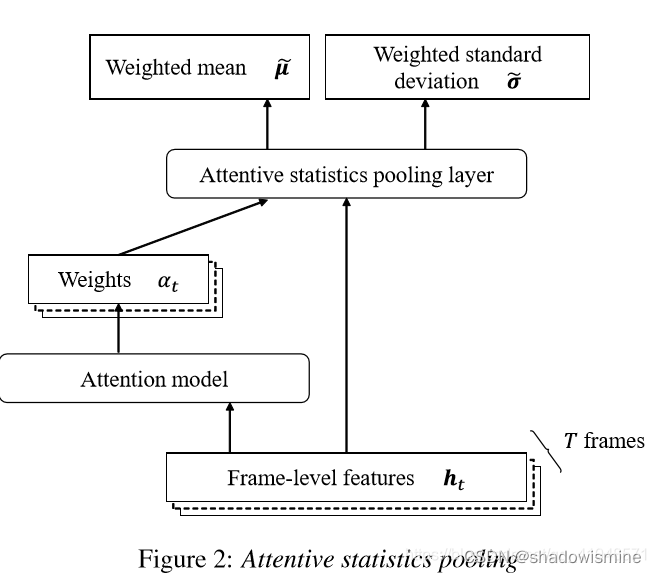
2. Attentive Statistics Pooling

链接：https://arxiv.org/pdf/1803.10963.pdf

在一段话中，往往某些帧的帧级特征比其他帧的特征更为独特重要，因此使用attention赋予每帧feature不同的权值。

其中f(.)代表非线性变换，如tanh or ReLU function。

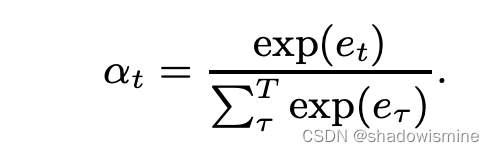
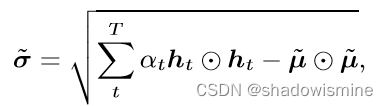
最后将每帧特征加劝求和

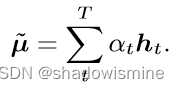
3. Self-Attentive pooling

链接：https://danielpovey.com/files/2018_interspeech_xvector_attention.pdf

4. Self Multi-Head Attention pooling

论文：Multi-Resolution Multi-Head Attention in Deep Speaker Embedding | IEEE Conference Publication | IEEE Xplore

5. NetVLAD

论文：

https://arxiv.org/pdf/1902.10107.pdf

https://arxiv.org/pdf/1511.07247.pdf

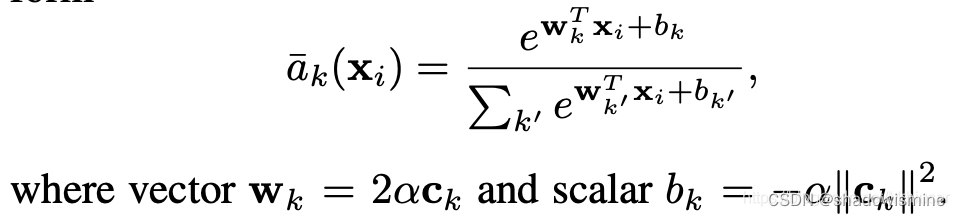
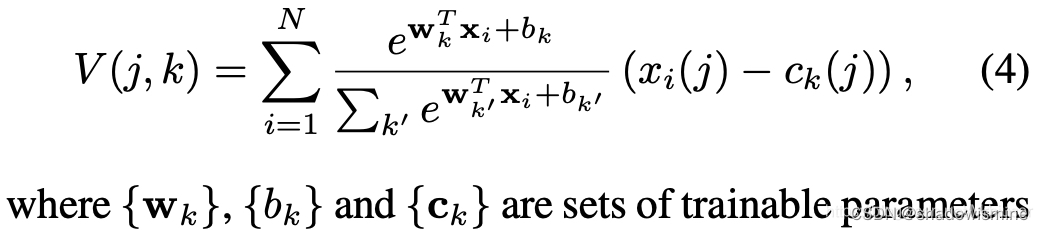
更详细的解释参考：从VLAD到NetVLAD，再到NeXtVlad - 知乎

6. Learnable Dictionary Encoding (LDE)

论文：https://arxiv.org/pdf/1804.05160.pdf

we introduce two groups of learnable parameters. One is the dictionary component center, noted as µ = {µ1, µ2 · · · µc}. The other one is assigned weights, noted as w.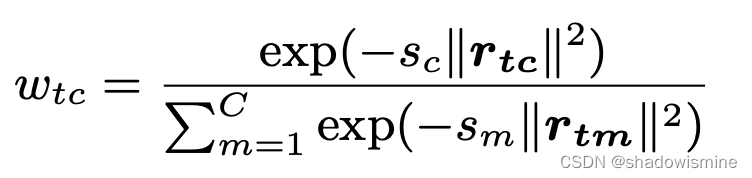

where the smoothing factor $s_c$ for each dictionary center $u_c$ is learnable.

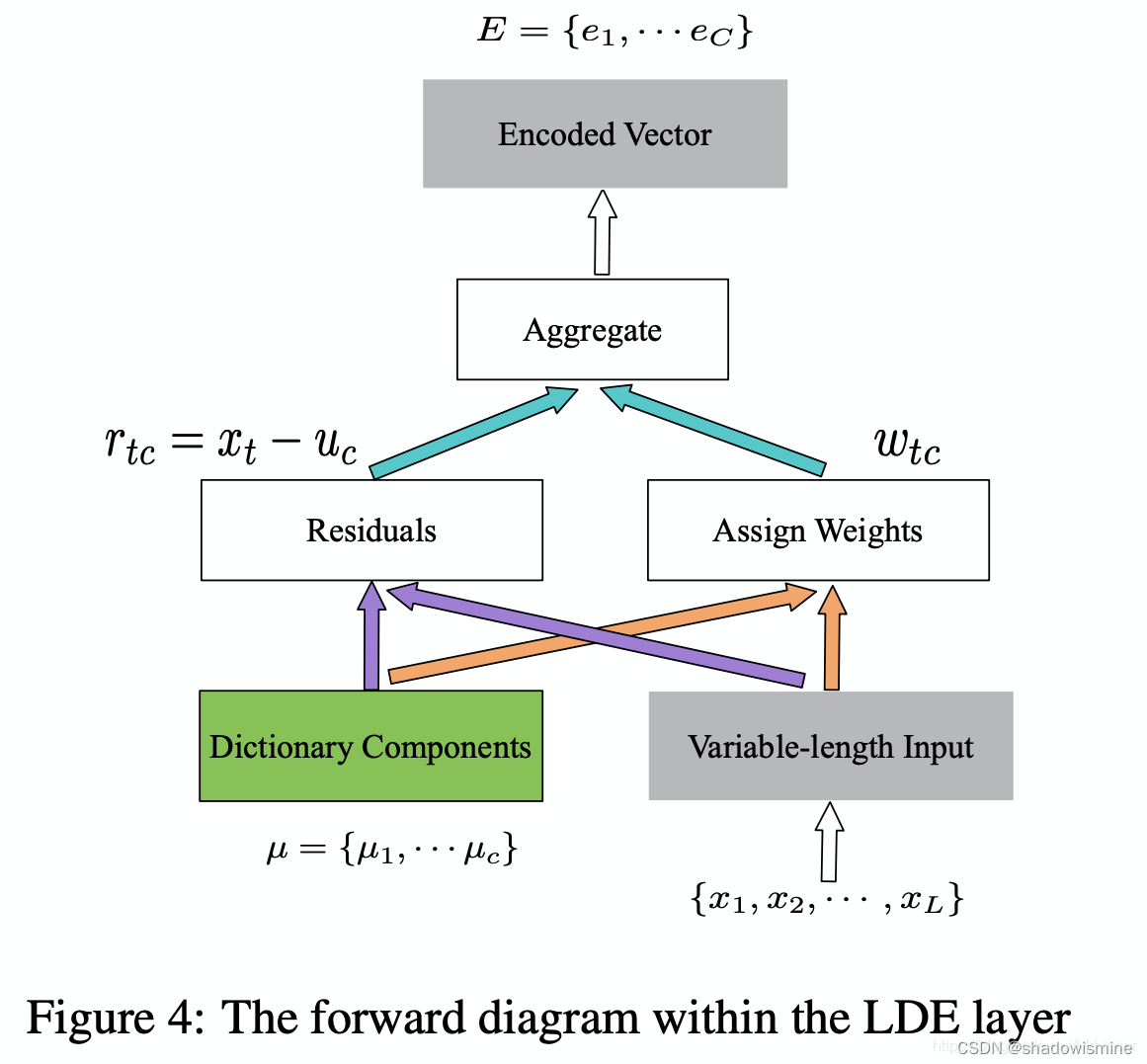
7. Attentive Bilinear Pooling (ABP) - Interspeech 2020

论文：https://www.isca-speech.org/archive/Interspeech_2020/pdfs/1922.pdf

Let $H \in \mathbb{R}^{L\times D}$ be the frame-level feature map captured by the hidden layer below the self-attention layer, where L and D are the number of frames and feature dimension respectively. Then the attention map $A \in \mathbb{R}^{K\times L}$ can be obtained by feeding H into a 1×1 convolutional layer followed by softmax non-linear activation, where K is the number of attention heads. The 1st-order and 2nd-order attentive statistics of H, denoted by µ and $\sigma ^{2}$ , can be computed similar as crosslayer bilinear pooling, which is

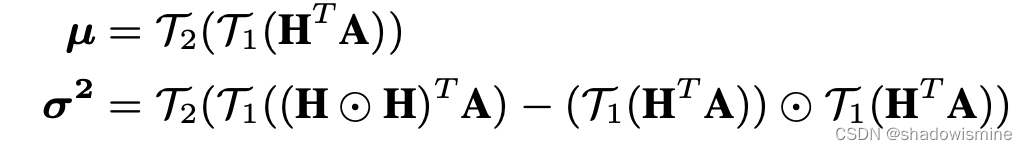
where T1(x) is the operation of reshaping x into a vector, and T2(x) includes a signed square-root step and a L2- normalization step. The output of ABP is the concatenation of µ and $\sigma ^{2}$

8. Short-time Spectral Pooling (STSP) - ICASSP 2021

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9414094&tag=1https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9414094&tag=1From a Fourier perspective, statistics pooling only exploits the DC (zero-frequency) components in the spectral domain, whereas STSP incorporates more spectral components besides the DC ones during aggregation and is able to retain richer speaker information.

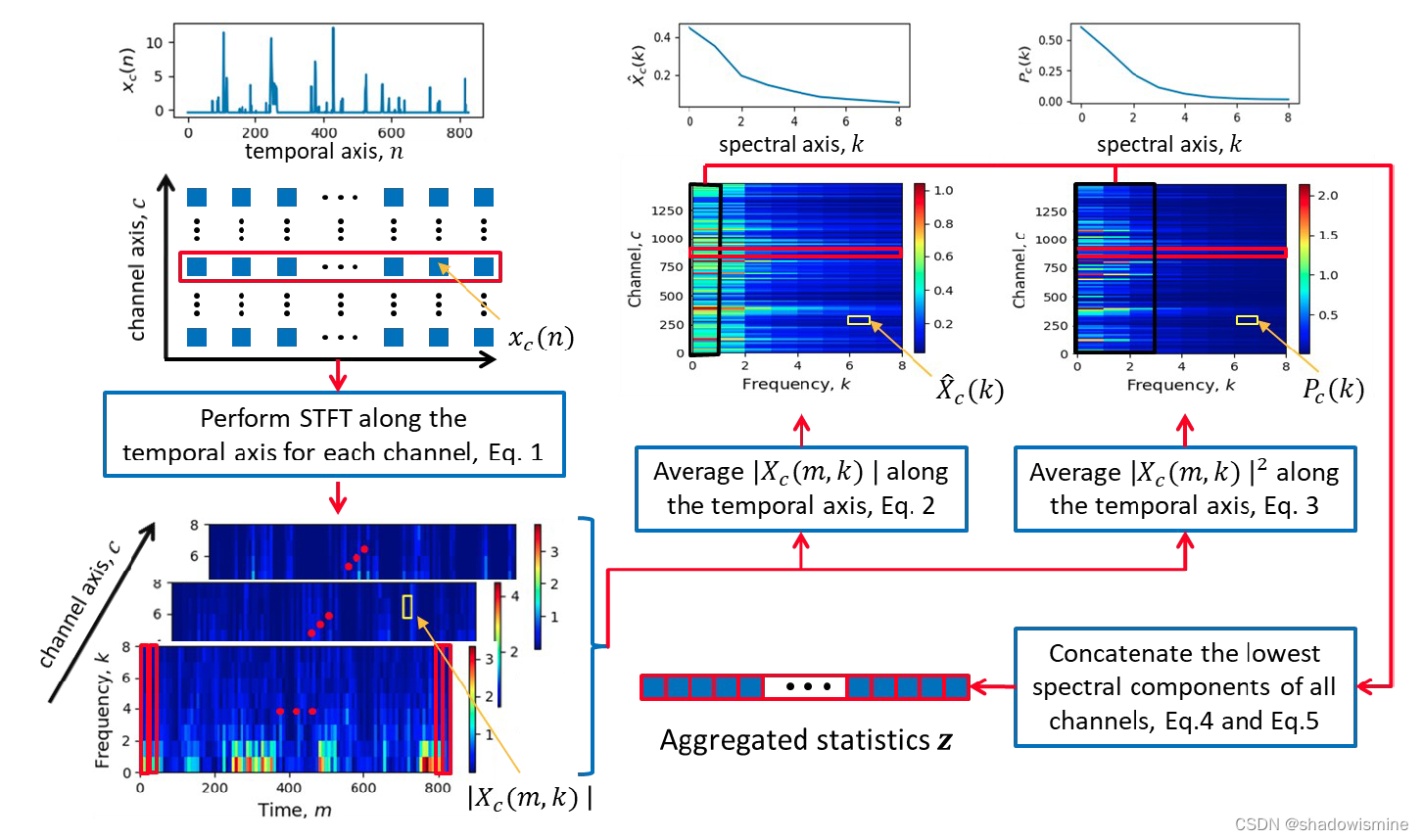
1. 将卷积层提取到的特征做STFT（Short Time Fourier Transorm）,每一个channel得到一个二维频谱图。

2. 计算averaged spectral array

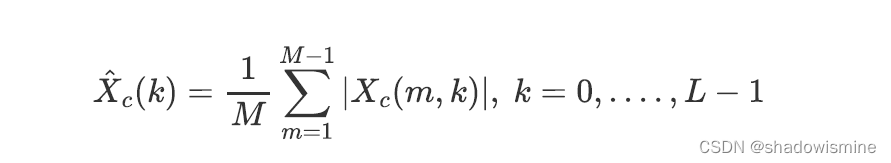
3. 计算second-order spectral statistics

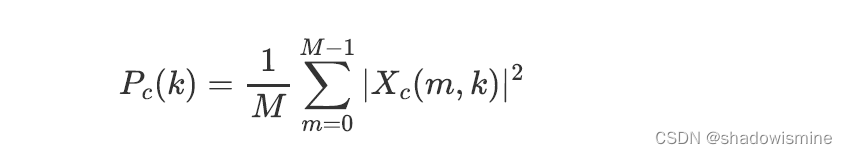
4. 将两个特征进行拼接（C is the number of channels）

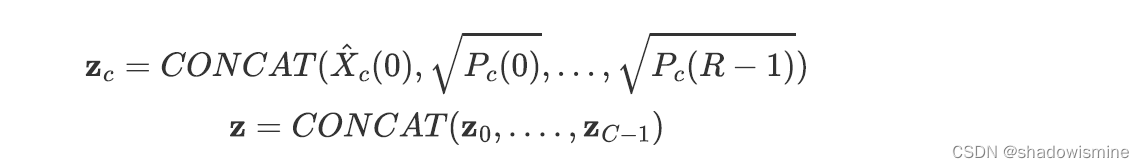
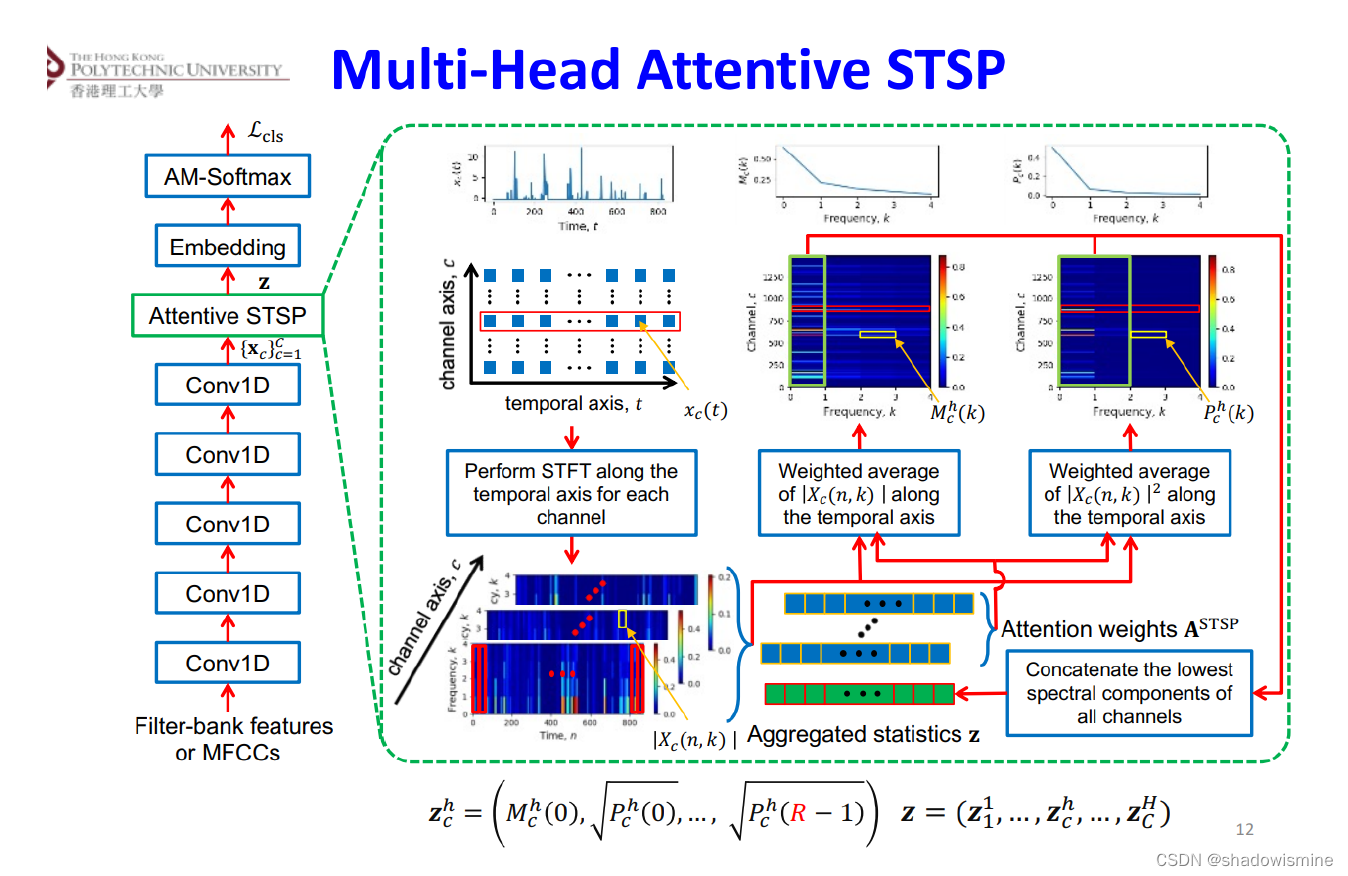
9. Multi-head attentive STSP （IEEE TRANS. ON AUDIO, SPEECH, AND LANGUAGE PROCESSING 2022）

One limitation of STSP is that the brute average of the spectrograms along the temporal axis ignores the importance of individual windowed segments when computing the spectral representations. In other words, all segments in a specific spectrogram were treated with equal importance.