力扣日记：【二叉树篇】98. 验证二叉搜索树

日期：2023.12.21
参考：代码随想录、力扣

98. 验证二叉搜索树

题目描述

难度：中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

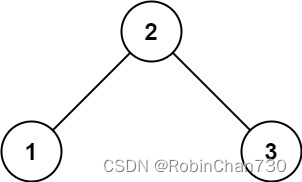
输入：root = [2,1,3]
输出：true

示例 2：

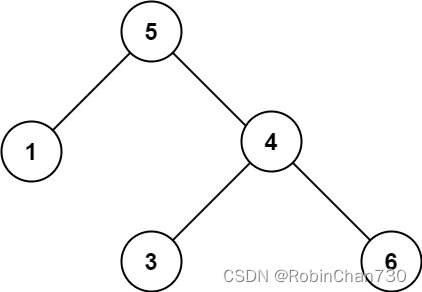
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 10^4] 内
• -2^31 <= Node.val <= 2^31 - 1

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
#define SOLUTION 2
public:
#if SOLUTION == 0
    // 下面代码有问题，搞不定了。。。
    /*
    bool isValidBST(TreeNode* root) {
        if (root == nullptr)    return false;
        // 需要先对根节点进行处理
        if (root->left != nullptr && root->left->val >= root->val)  return false;
        if (root->right != nullptr && root->right->val <= root->val)    return false;
        // 根节点暂且满足条件，递归判断其子树  
        return traversal(root->left, root->val, true) && traversal(root->right, root->val, false);
    }
    // 参数为当前子树的根节点，以及该子树的父节点的值，以及该子树是左子树还是右子树，返回值为该子树是否为二叉搜索树
    bool traversal(TreeNode* root, int midNodeVal, bool leftTree) {
        if (root == nullptr)    return true;
        // 左为空，则左不为false
        // 左不为空, 
        if (root->left != nullptr) {
            // 首先判断左子节点
            if (root->left->val >= root->val)   return false;
            if (!leftTree) {
                // 如果是右子树，还要保证其左节点比该子树的父节点大
                if (root->left->val <= midNodeVal)  return false;
            }
        }  
        if (root->right != nullptr) {
            // 首先判断右子节点
            if (root->right->val <= root->val)  return false;
            if (leftTree) {
                // 如果是左子树，要保证其右节点比该子树的父节点小
                if (root->right->val >= midNodeVal) return false;
            }
        }
        // 遍历左右节点
        bool left = traversal(root->left, root->val, true);
        if (left == false)  return false;
        bool right = traversal(root->right, root->val, false);
        return right;
    }
    */
#elif SOLUTION == 1
    // 思路：利用二叉搜索树的特性！！！
    // 二叉搜索树中序遍历是有序的！！！
    // 方式1：先转换为数组，再判断数组是否有序
    bool isValidBST(TreeNode* root) {
        // 先中序遍历得到数组
        vector<int> result;
        traversal(root, result);
        // 对数组进行判断
        // 如果数组为空或只有1个，则为true(空的树也为二叉搜索树！)
        if (result.size() <= 1) return true;
        // size >= 2
        // 遍历数组
        for (int i = 1; i < result.size(); i++) {
            // 如果后面的元素 <= 前面的元素(注意也不能相等)，则不是二叉搜索树
            if (result[i] <= result[i-1])   return false;
        }
        return true;
    }
    // 中序遍历：左中右
    void traversal(TreeNode* root, vector<int>& result) {
        if (root == nullptr)   return;
        // 左
        traversal(root->left, result);
        // 中
        result.push_back(root->val);
        // 右
        traversal(root->right, result);
    }
#elif SOLUTION == 2
    // 方式2：直接在进行中序遍历的同时判断是否有序
    TreeNode* pre = nullptr;    // 保存上一个节点（用来比较）
    bool isValidBST(TreeNode* root) {
        // 空，直接返回true
        if (root == nullptr)    return true;
        // 左
        bool left = isValidBST(root->left);
        if (left == false)  return false;
        // 中
        // 如果pre不为空，当前节点值需要比上一个节点值大
        if (pre != nullptr && root->val <= pre->val)    return false;   // false 则不需要继续迭代了也不需要更新pre了
        // 如果没有违反，更新pre，并继续递归
        pre = root;
        // 右
        bool right = isValidBST(root->right);
        return right;
    }
#endif
};

复杂度

时间复杂度：
空间复杂度：

思路总结

• 本题就像是脑筋急转弯，得从二叉搜索树转到这样一个思路：
• 如果一棵树是二叉搜索树，其中序遍历一定是有序的！！！（从小到大）
• 因此，本题有两种方式来验证：
  • 方式1：先用中序遍历（左中右）得到遍历数组；再对数组判断是否有序（较简单）
  • 方式2：直接在中序遍历的同时判断是否有序（需要在递归中保存上一个值，稍复杂）