题意理解：

        给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

        每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。

        还是从初始坐标i=0的位置到达最后一个元素，但是问题不是能不能跳到，而是最少几步能跳到最后一个元素。

        目标：求跳到末尾元素的最小步数。

解题思路：

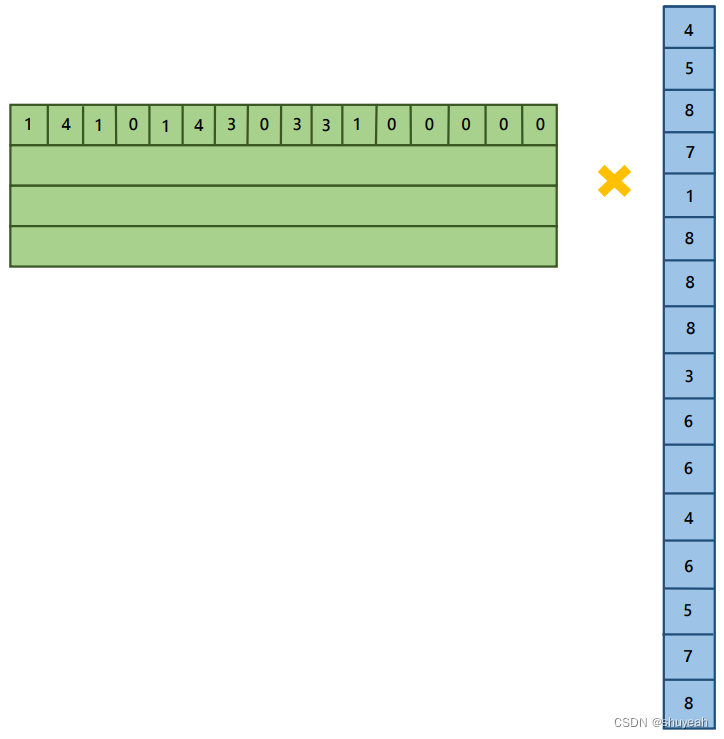
 如上面的例子所示：

        两种方式都能跳到末尾，但是最小步数是2.

        要用贪心法解题，就要明确什么是局部最优，什么是全局最优。

        这道题里，全局最优：到达末尾元素步数尽可能小，则要求每步尽可能大一些。

        所以局部最优为：使当前步，尽可能的跳到较远的位置上。

        我们使用两个量：cur表达当前能到达的最远距离，next表达下一步能到达的最远距离。

        我们在这个cur范围内挑选第二步，让两步尽可能达到尽可能远的位置。

1.贪心解题

我们用count来记录步数，cur来记录当前可达的最远位置,next表达下一步能到达的最远位置。

若再探索一步就覆盖到末尾元素，则count+1,结束

若再探索最远一步仍就到不了末尾元素，则count++,探索下下一步的最远位置。

class Solution {
    public int jump(int[] nums) {
        if(nums.length==1) return 0;//只有一个末尾元素，不用走也能到
        int count=0;
        int cur=0;
        int next=0;
        for(int i=0;i<nums.length;i++){
            next=Math.max(next,i+nums[i]);
            //当前步探索位置到达边界
            if(next>=nums.length-1){
                count++;
                break;
            }
            if(i==cur){
                count++;
                cur=next;
            }
        }
        return count;
    }
}

2.分析

时间复杂度：O(n)

空间复杂度：O(n)

n为输入数组的长度。