接上期信号处理基础之噪声与降噪(一) | 噪声分类及python代码实现，本期为大家介绍噪声评价指标，并且讲解两种降噪方法——平滑降噪、SVD降噪，并给出python代码。

1 噪声评价指标

1.1 信噪比

信噪比（Signal-to-noise ratio, SNR），指信号功率与噪声功率的比，也为幅度平方的比，信噪比是衡量降噪程度最直观的量，信噪比越大，信号中包含的噪声越少，降噪效果越明显。对于信号 ，SNR可表示为：

一般地，用分贝对信噪比进行度量，可表示为

注：
①上述 指准备求信噪比的有用信号，有用信号通常指的是纯净信号；
②上述 指纯噪声，指的是滤波后的信号减去纯净信号，并不是滤波后的信号减去滤波前的信号。

1.2 波形相似参数

波形相似系数（Normalized Correlation Cofficient, NCC）反映去噪前后信号波形的整体相似度，不能表征波形震荡变化的细节，NCC越接近1，信号之间的相关性越高，其可表示为：

1.3 均方误差

均方误差（Mean-Square Error, MSE）是衡量”平均误差“的较为方便的方法，可以评价数据的变化程度，均方误差可反应去噪前后信号的差异程度，MSE越小，说明降噪效果越好。MSE可表示为：

1.4 均方根误差

均方根误差（Root Mean Square Error, RMSE）也称方均根偏移，是一种常用的测量数值之间差异的量度，RMES越小，降噪效果越好。RMSE可表示为：

1.5 python代码实现

import numpy as np
def denoise_evaluate(signal_pure, noise, signal_denoised):
    value = {}    # SNR计算
    p_signal = np.sum(signal_pure**2) / len(signal_pure)    
    p_noise = np.sum(noise**2) / len(noise)    
    SNR = 10 * np.log10(p_signal / p_noise)    
    value['SNR'] = SNR    
    # NCC计算    
    NCC = np.correlate(signal_pure, signal_denoised) / (np.linalg.norm(signal_pure) * np.linalg.norm(signal_denoised))    value['NCC'] = NCC[0]    
    # MSE计算    
    MSE = np.mean((signal_pure - signal_denoised) ** 2)    
    value['MSE'] = MSE    
    # RMSE计算    
    RMSE = np.sqrt(MSE)    
    value['RMSE'] = RMSE    
    return value

注：上述四个指标的计算均依赖于”纯净信号“，对于只知道真是含噪信号，不知道纯净信号的情况，无法进行计算，即对于工程实际中的随机信号，无法直接用上述四个指标进行衡量。

2 平滑降噪

2.1 滑动平均的基本原理

滑动平均（Moving Average）是一种时域滤波方法，其基本原理是设定一个滑动窗口，该滑动窗口沿着原始数据时序方向移动，每次移动时计算当前窗口的平均值作为滤波值，最终得到滑动平均序列，其过程可表示为下图。

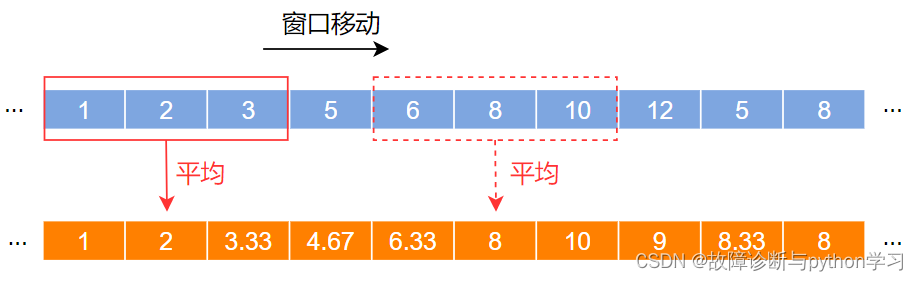
记滑动窗口长度为N（N为奇数），则滑动平均可表示为：

滑动窗口为对称窗口，防止出现相位偏差，窗口长度一般为奇数。特别地，滑动平均的滤波效果取决于滑动窗的长度，一般长度越大平滑效果越好，但窗口选择过大可能出现过平滑，湮没有效信号，且滑动平均滤波对边缘数据的处理效果不佳。

注：也可通过卷积的方式实现滑动滤波，此处不展开讨论

2.2 SG滤波基本原理

SG(Savitzky-Golay)滤波是一种广泛使用的数据平滑滤波降噪方法，其基于曲线局部特征进行多项式拟合，应用最小二乘法确定加权系数进行移动窗口加权平均，重构的数据能够较好保留局部特征，不受时间及空间尺度的影响。SG滤波的基本公式可表示为：

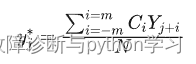
具体地，记滤波窗口长度为 （ 为奇数），测量点记为 ，采用 次多项式对窗口内的数据点进行拟合，记拟合常数为 ，则有滤波结果

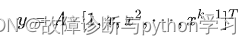
不难发现，在使用SG滤波进行降噪时，窗口长度 ，多项式拟合阶次 对降噪结果起着至关重要的作用。窗口长度越长，单次参与拟合的数据量越多，多项式拟合阶次越高，单次拟合的结果越接近原始信号，保留的细节越多，但是过高的阶次可能出现过拟合，产生新的噪声。
注：限于篇幅，不对完整过程进行推导，详细过程请参考文献[3]。

2.3 python实现

本文给出了3种方法，常规方法滤波、卷积平滑滤波、SG滤波。

def moving_average(data, window_size):
    # 常规方法进行平滑滤波    
    smoothed_data = []    
    for i in range(len(data)):        
    start = max(0, i - window_size // 2)        
    end = min(len(data), i + window_size // 2 + 1)        
    window = data[start:end]        
    smoothed_data.append(sum(window) / len(window))    
    return smoothed_data

import numpy as np
def moving_average_conv(data, window_size):    
   # 卷积平滑滤波    
   window = np.ones(window_size) / window_size    
   smoothed_data = np.convolve(data, window, mode='same')    
   return smoothed_data

import numpy as npfrom scipy 
import signal
def moving_average_sg(data, window_size, order):    
  # SG滤波
  sg_data = signal.savgol_filter(data, window_size, order)    
  return sg_data

3 SVD降噪

3.1 SVD降噪的基本原理

奇异值分解(Singular Value Decomposition, SVD)能够对矩阵进行分解，得到代表矩阵最本质变化的矩阵元素。作为信号处理的重点研究方向之一，其主要功能是去除信号中的随机噪声，降噪后的信号不存在时间延迟且相移较小。

记一个含噪声的时间序列 ， 表示为理想信号 和噪声信号 的和，表示为

将 构造成Hankel矩阵（含噪矩阵 ），表示为：

式中，当 为偶数时， ， 为奇数时， ， 。
对含噪矩阵 进行奇异值分解可得：

其中 矩阵 的奇异值， ， 为零矩阵， 为正交矩阵。
选取有效奇异值个数 ，保留主对角矩阵 的前 个较大的奇异值，将其余奇异值全部置为0，得到新的对角矩阵：

于是可以通过左右正交矩阵U和V得到新的信号矩阵 ，将重构的矩阵 恢复成一维信号，此时便完成了SVD降噪处理。

3.2 python实现

import numpy as np
from numpy.linalg import svd
def denoised_with_svd(data, nlevel=8):
  """
  :param data: 需要降噪的原始数据，1D-array    
  :param nlevel: 阶次    
  :return:重构后的信号    
  """    
  N = len(data)    
  A = np.lib.stride_tricks.sliding_window_view(data, (N//2,))    
  U, S, Vh = svd(A)    
  # 重构信号    
  X = np.zeros_like(A)    
  for i in range(nlevel):    
      X += Vh[i, :] * S[i] * U[:, i:i+1]    
      X = X.T    data_recon = np.zeros(N)    
      for i in range(N):    
          a = 0        
          m = 0        
          for j1 in range(N//2):       
              for j2 in range(N//2+1):           
                  if i == j1 + j2:                  
                     a = a + X[j1, j2]  # 把矩阵重构回一维信号                    
                     m = m + 1        
           if m != 0:            
              data_recon[i] = a / m    
    return data_recon

4 算例测试

4.1 测试用例

import matplotlib.pyplot as plt
import matplotlib
# 测试用例
n = 500  # 生成500个点的信号
t = np.linspace(0, 30*np.pi, n, endpoint=False)
s = np.cos(0.1*np.pi*t) + np.sin(0.3*np.pi*t) + np.cos(0.5*np.pi*t) + np.sin(0.7*np.pi*t)  # 原始信号
r = np.random.randn(n)
y = s + r  # 加噪声
data_smooth_avg = moving_average(y, 5)
data_smooth_conv = moving_average_conv(y, 5)
data_smooth_sg = moving_average_sg(y, 5, 3)
data_svd = denoised_with_svd(y)
fig = plt.figure(figsize=(16, 9))
plt.subplots_adjust(hspace=0.5)
font = {'family': 'Times New Roman', 'size': 16, 'weight': 'normal',}
matplotlib.rc('font', **font)
plt.subplot(6, 1, 1)
plt.plot(s, linewidth=1.5, color='b')
plt.title('原始模拟信号', fontname='microsoft yahei', fontsize=16)
plt.subplot(6, 1, 2)
plt.plot(y, linewidth=1.5, color='r')
plt.title('原始模拟信号+高斯噪声', fontname='microsoft yahei', fontsize=16)
plt.subplot(6, 1, 3)
plt.plot(data_smooth, linewidth=1.5, color='g')
plt.title('降噪信号-均值法', fontname='microsoft yahei', fontsize=16)
plt.subplot(6, 1, 4)
plt.plot(data_smooth, linewidth=1.5, color='g')
plt.title('降噪信号-卷积法', fontname='microsoft yahei', fontsize=16)
plt.subplot(6, 1, 5)
plt.plot(data_smooth, linewidth=1.5, color='g')
plt.title('降噪信号-SG滤波', fontname='microsoft yahei', fontsize=16)
plt.subplot(6, 1, 6)
plt.plot(data_svd, linewidth=1.5, color='g')
plt.title('降噪信号-SVD', fontname='microsoft yahei', fontsize=16)

4.2 降噪结果

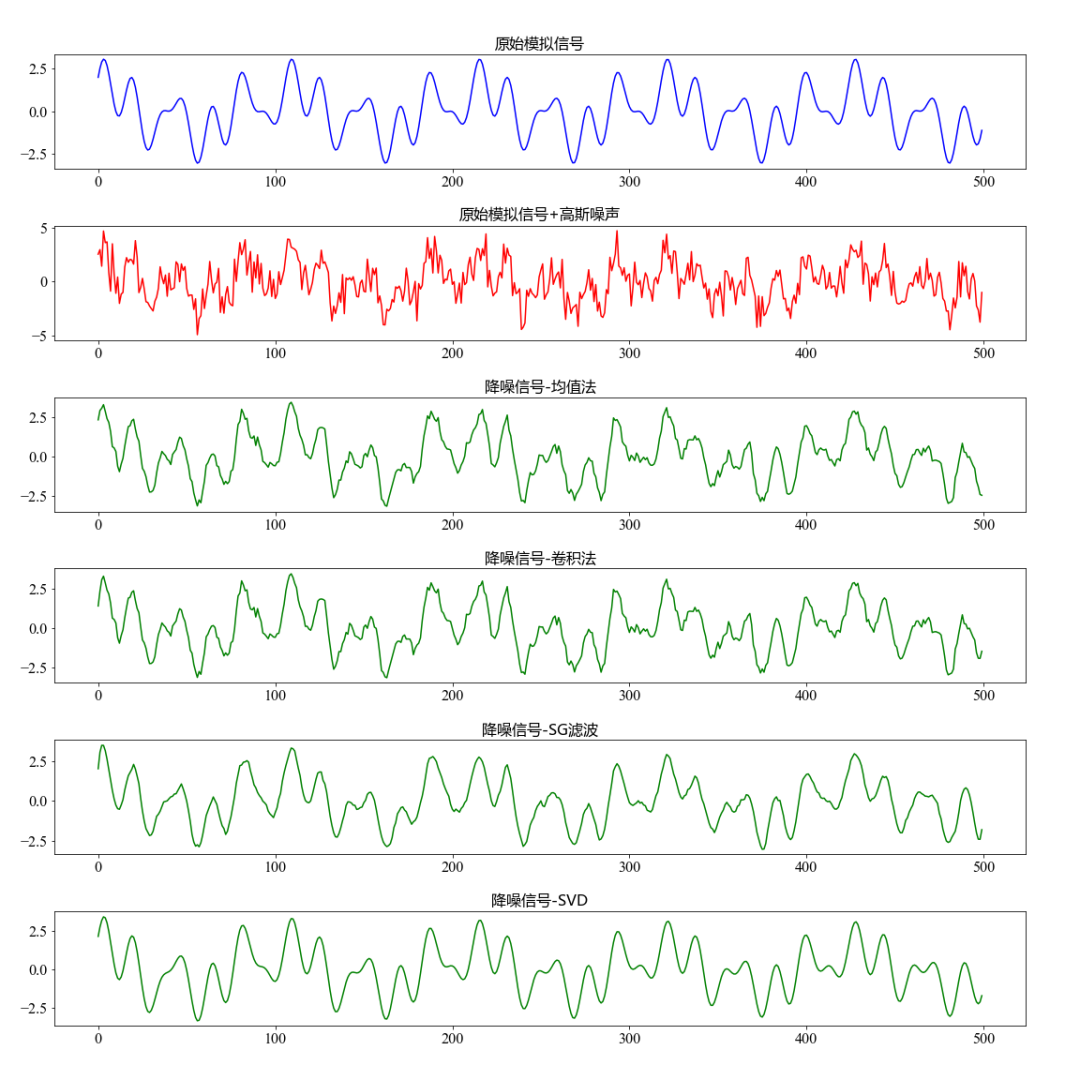
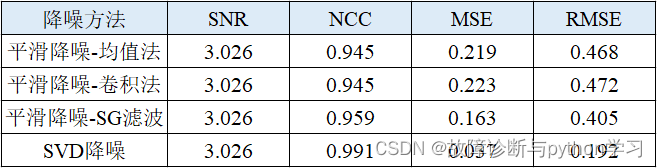
4.3 降噪指标对比

5 参考文献

[1]https://zhuanlan.zhihu.com/p/558808890
[2]https://zhuanlan.zhihu.com/p/579187348
[3]https://blog.csdn.net/weixin_36815313/article/details/121238628
[4]刘子涵. 噪声背景下基于时频分析的滚动轴承微弱故障诊断方法研究[D]. 河北:燕山大学,2021.

往期推荐

关注公众号《故障诊断与python学习》，了解更多故障诊断干货
往期推荐

[1] 故障诊断代码实战之第1期 | 手把手教你安装python环境(Anaconda)及跑通第一个信号处理案例！！！

[2] 机械故障诊断信号的幅域分析 - 时域统计特征 | 基于python的代码实现，在CWRU和IMF轴承数据集上实战

[3] 机械故障诊断信号的幅域分析 - 幅值概率密度函数 | 基于python的代码实现，在CWRU轴承数据上实战

[4] Python学习｜第1篇，用python读取CWRU数据集