二进制 :
也就是只有0和1的进制表示 ;
二进制枚举算法
- 一个二进制数 x 可以表示 S 的一个子集,某个二进制位i上为0表示没有选i元素,为1表示选了该元素放入子集,比如13为1101就表示选了0,2,3号元素;
- 对于一个长度为N的序列(也就是包含N个元素)有2^N个子集,因为每个二进制位有两种可能,然后有n个二进制位,所以组合方案数就是2 ^ N 种;
- 用位运算来表示的话,也就是 (1 << N) 种,表示1 左移N位,大小是2 ^ N ,那么枚举也就是
-
for(int i = 0; i < (1<<n); i++) - 然后可以用 x&(1<<i) 来判断当前子集有没有选i元素,&表示与运算,同一为一,不同为0;
- 选取第一、三、四、六、七件物品 1101101(2)=109(10)
- 109&(1<<3)==1 说明 109 对应的子集(选取方案)中包含编号为 3 (第 4 个)元素。
- 109&(1<<4)==0 说明 109 对应的子集(选取方案)中不包含编号为 4 (第 5 个)元素。
输出一个数x的对应子集中所有的元素
for(int i=0;i<n;i++)
if(x&(1<<i))
cout<<i<<endl;枚举所有子集
for(int i = 0; i < (1<<n); i++){
xxxxxx..
}枚举0-2^n-1的每一个状态
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
for(int i = 0; i < (1<<n); i++) //从0~2^n-1个状态 1 左移 n 位
{
printf("%d : ",i) ;
for(int j = 0; j < n; j++)
{
if(i & (1 << j))
{
printf("%d ",j);
}
}
printf("\n");
}
return 0;
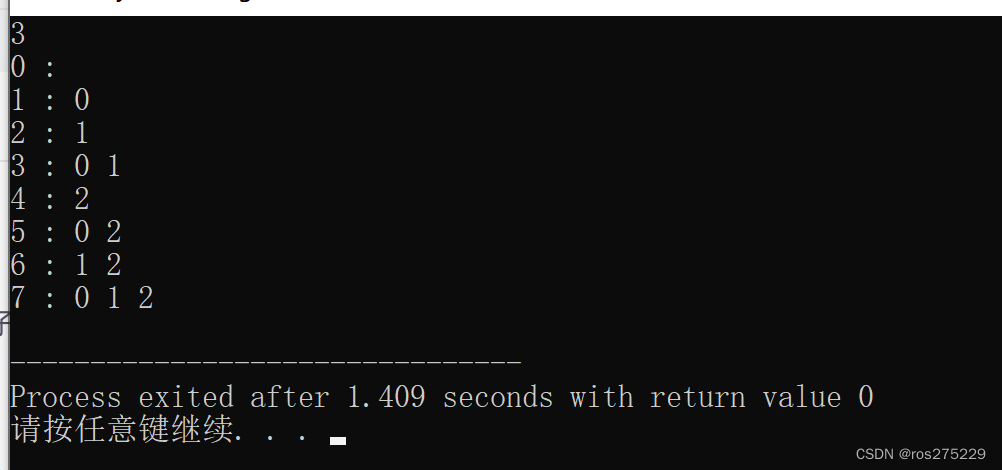
}运行效果 :
参考 :
二进制集合操作 - OI Wiki