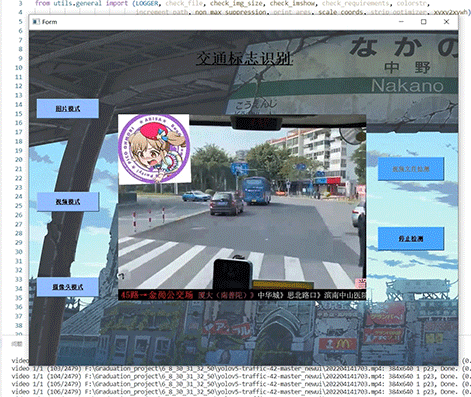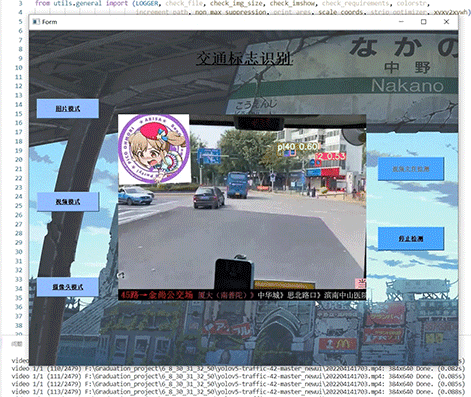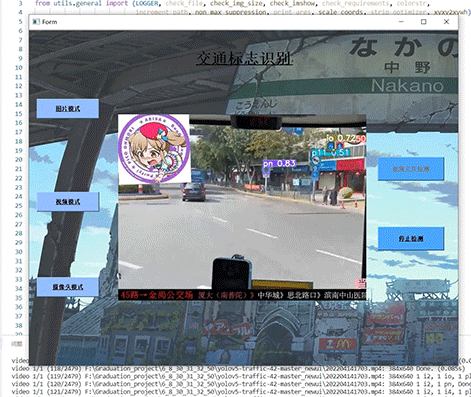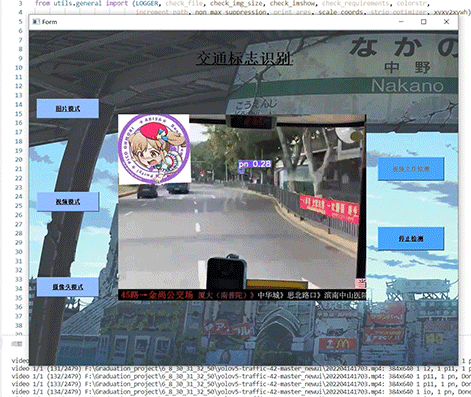
问题描述：

走n阶台阶，每次可以选择走一阶或者走两阶，那么一共有多少种走法？输入包含一个整数n (1 ≤ n ≤ 30)输出一个整数，即小乐乐可以走的方法数。

分析：

这是一个数学问题，本质是要求列举所有的结果个数，求结果个数用递归。我们把整个步数拆解为大量小问题。
首先，我们根据题目可以得出，大数字拆解到最后，各个小数字会在0、1、2三个结果里面出现，每个小数字分别对应0、1、2三种走法；我们不妨倒过来想，我们输入的数字本身就是由0、1、2三个数字组成的，以此我们可以设立3个返回值，把所有的情况的值返回去，最后集中相加即可得到所有的可能数量。

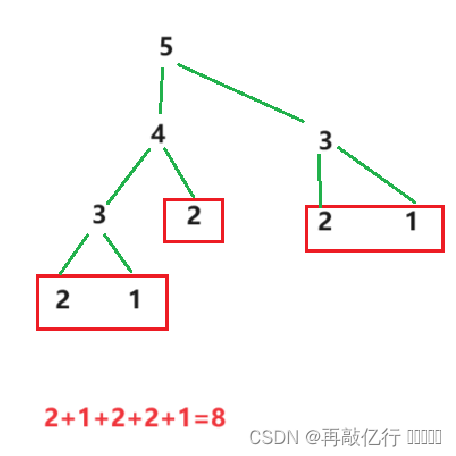
代码如下：

#include <stdio.h>
//求多少种走法，是数学问题，用
//思路：知道阶数后我们可以使用循环的方法穷举所有的方法种类
//解决方案：递归
int foot(int n)
{
    if (n == 2)
        return 2;
    if (n == 1)
        return 1;
    if (n == 0)
        return 0;
    return (foot(n - 1) + foot(n - 2));
}
int main()
{
    int foot(int i);

    int n = 0;
    scanf("%d", &n);
    printf("%d", foot(n));
    return 0;
}