《博主简介》
小伙伴们好,我是阿旭。专注于人工智能AI、python、计算机视觉相关分享研究。
✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~
👍感谢小伙伴们点赞、关注!
X的平方根
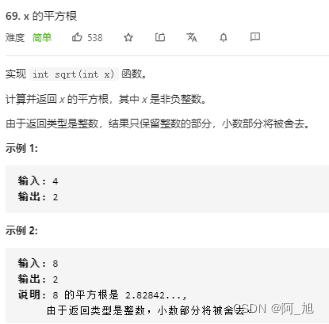
| class Solution: def mySqrt(self, x: int) -> int: l, r, ans = 0, x, -1 while l <= r: mid = (l + r) // 2 if mid * mid <= x: ans = mid l = mid + 1 else: r = mid - 1 return ans |
有效完全平方数
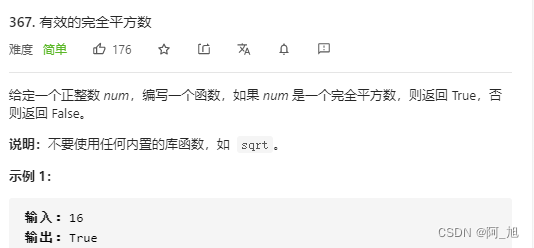
| class Solution: def isPerfectSquare(self, num: int) -> bool: l = 0 r = num while l <= r: mid = (l+r)//2 if mid * mid == num: return True elif mid * mid < num: l = mid + 1 else: r = mid - 1 return False |
搜索旋转排序数组

| class Solution: def search(self, nums: List[int], target: int) -> int: if not nums: return -1 # 二分法 n = len(nums) left = 0 right = n - 1 while left <= right: mid = (left + right) // 2 if nums[mid] == target: return mid if nums[0] <= nums[mid]: # 说明左边有序 if nums[0] <= target < nums[mid]: right = mid - 1 else: left = mid + 1 else: # 右边有序 if nums[mid] < target <= nums[n-1]: left = mid + 1 else: right = mid - 1 return -1 |
搜索二位矩阵

| class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: if not matrix: return False # 二分查找 row = index // n ; col = index % n m = len(matrix) n = len(matrix[0]) left = 0 right = m * n - 1 while left <= right: mid = (left + right) // 2 cur_m = mid // n cur_n = mid % n if matrix[cur_m][cur_n] == target: return True elif matrix[cur_m][cur_n] > target: right = mid - 1 else: left = mid + 1 return False |
搜索二维矩阵2

| def searchMatrix(self, matrix, target): """ :type matrix: List[List[int]] :type target: int :rtype: bool """ # 1.暴力法 for i in range(m) for j in range(n) O(mn) # 2.剪枝搜索,假设从左下角开始搜索O(m+n) if not matrix: return False m = len(matrix) n = len(matrix[0]) row = m - 1 col = 0 while row >= 0 and col < n: if matrix[row][col] > target: row -= 1 elif matrix[row][col] < target: col += 1 else: return True return False |
寻找旋转排序数组中的最小值

| class Solution: def findMin(self, nums: List[int]) -> int: if len(nums) == 1: return nums[0] left = 0 right = len(nums) - 1 while left < right: mid = (left + right) // 2 if nums[mid] < nums[right]: # mid可能是最小值 right = mid else: # mid一定不是最小值 left = mid + 1 return nums[left] |
关于本篇文章大家有任何建议或意见,欢迎在评论区留言交流!
觉得不错的小伙伴,感谢点赞、关注加收藏哦!
欢迎关注下方GZH:阿旭算法与机器学习,共同学习交流~