欲穷千里目,更上一层楼。
一个空间的混乱在更高维度的空间往往意味着秩序。
Machine-Learning: 《机器学习必修课:经典算法与Python实战》配套代码 - Gitee.com
1、核心思想及原理
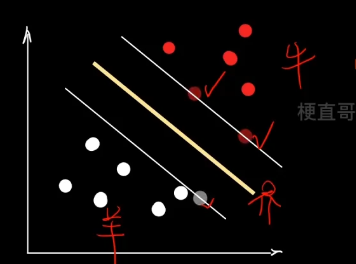
针对线性模型中分类两类点的直线如何确定。这是一个ill-posed problem。
线性模型通过求解各点距离进行投票,可以使用sigmoid函数来求解总损失,转换成一个最优化问题。但是模型泛化能力太差,很容易受到噪声的干扰,直线可能会发生很大变化。
所以我们更想让直线靠近中间位置。

三个概念:
支持向量 support vector —— 距离决策边界最近的点,每个类别的极端数据点
超平面 hyperplane —— “隔离带”中间的平分线
间隔 margin —— 最大化margin
民主集中的思想 ~

2、线性SVM —— 硬间隔 Hard Margin
(假定数据本身线性可分)
通过上一小节我们得到优化目标:
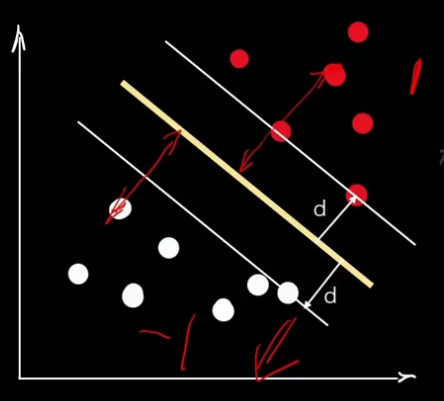
最大化间隔margin 也就是 最大化距离 d,也就是点到超平面的垂直距离。
注意此处的距离和线性模型中的距离不同,线性模型中的距离是 yhat-y (斜边)

SVM的求解过程和线性方程一样:
先假设一个超平面,
这里的W和X都是高维向量,点到高维空间中的距离有现成公式可以套用:
||w||为w的范数,表示高维空间中长度的概念。
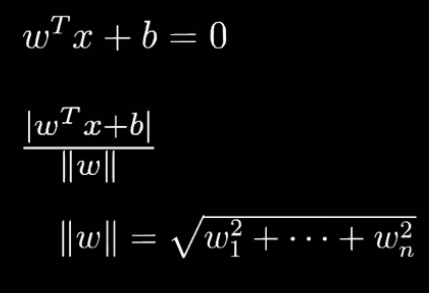
有了这样一个距离公式,隔离带就可以表示为一个分段函数的形式。
我们用1和-1来表示两个类别:

现在我们给柿子两边同时除以d 变形,再继续整理做变量代换:
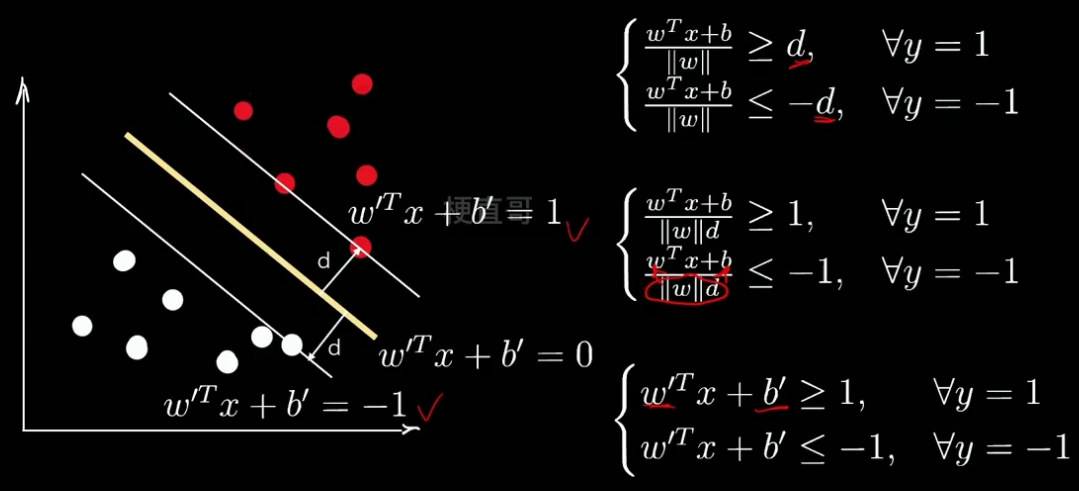
为了方便表示,看着撇多难受,我们再用w和b换回去,
但此时的w b和一开始推到时的w b,理论上已经不是同一个数了。
但是存在一个比例关系。在做一个变形:

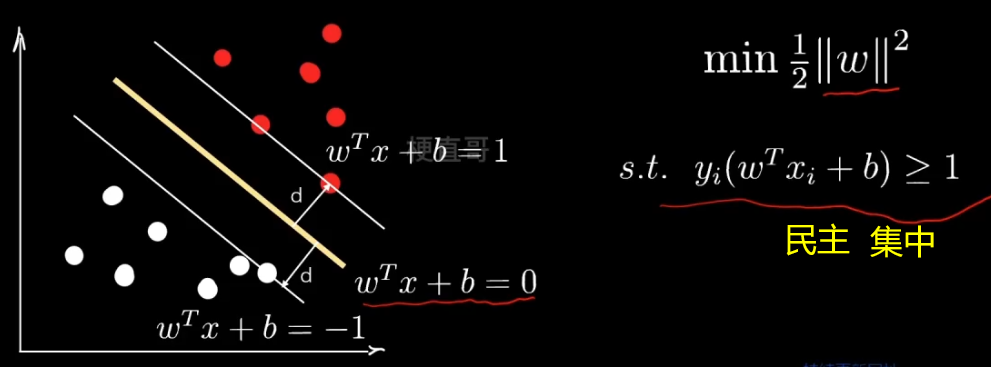
则现在的问题就简化为:

这是一个不等式约束的最优化问题。梯度下降只能用于无约束的最优化。
ps:
不等式约束最优化 引入 松弛变量 到等式约束最优化。
等式约束最优化 引入 拉格朗日乘子 到无约束最优化。
注意,这里的 i 是遍历所有的数据点。但在最小化范数时,我们只用到了支持向量。
但是如果你相信的人也出了问题呢?
3、线性SVM —— 软间隔 Soft Margin
软间隔要解决的问题:
异常值 outliner
支持向量的选择、民主集中思想的弱点
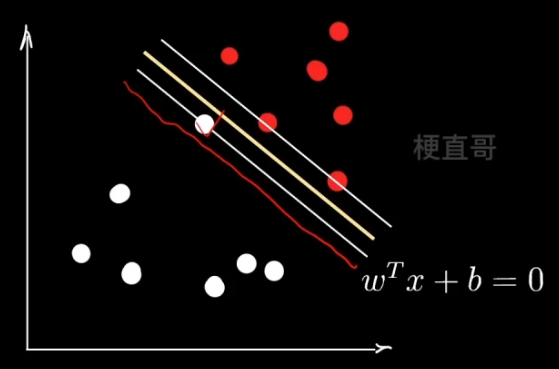
则需:建立容错机制,提升泛化能力
那么体现在数学上:允许点越过线一点点 ~

那么怎么保证 这个减去的值不能太大呢?

也就是说尽量让所有数据容错值的和最小。让二者取一个平衡。
C 就是一个新的超参数,用来调节两者的权重值。
再看一下这个求和的形式,是不是特别像正则化?其实就可以看成正则化。
正则化项是一次的,所以叫L1正则。这里省略了绝对值符号,因为其就是正数。

4、线性SVM代码实现
数据集
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_blobs
x, y = make_blobs(
n_samples=40,
centers=2,
random_state=0
)plt.scatter(x[:,0], x[:,1], c = y)
plt.show()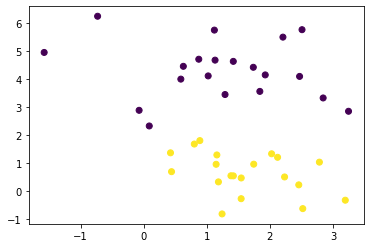
sklearn中的线性SVM
from sklearn.svm import LinearSVCclf = LinearSVC(C = 1)clf.fit(x, y)LinearSVC
LinearSVC(C=1)
clf.score(x, y)1.0
def decision_boundary_plot(X, y, clf):
axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
z = z.reshape(x1.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])
plt.contourf(x1, x2, z, cmap=custom_cmap)
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()decision_boundary_plot(x, y, clf)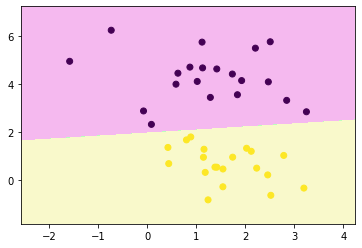
def plot_svm_margin(x, y, clf, ax = None):
from sklearn.inspection import DecisionBoundaryDisplay
DecisionBoundaryDisplay.from_estimator(
clf,
x,
ax = ax,
grid_resolution=50,
plot_method="contour",
colors="k",
levels=[-1, 0, 1],
alpha=0.5,
linestyles=["--", "-", "--"],
)
plt.scatter(x[:,0], x[:,1], c = y)plot_svm_margin(x, y, clf)
plt.show()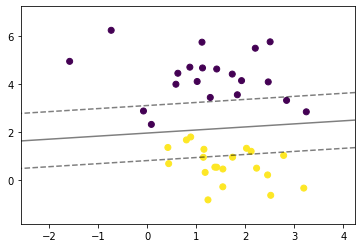
plt.rcParams["figure.figsize"] = (12, 8)
params = [0.1, 1, 10, 100]
for i, c in enumerate(params):
clf = LinearSVC(C = c, random_state=0)
clf.fit(x, y)
ax = plt.subplot(2, 2, i + 1)
plt.title("C: {0}".format(c))
plot_svm_margin(x, y, clf, ax)
plt.show()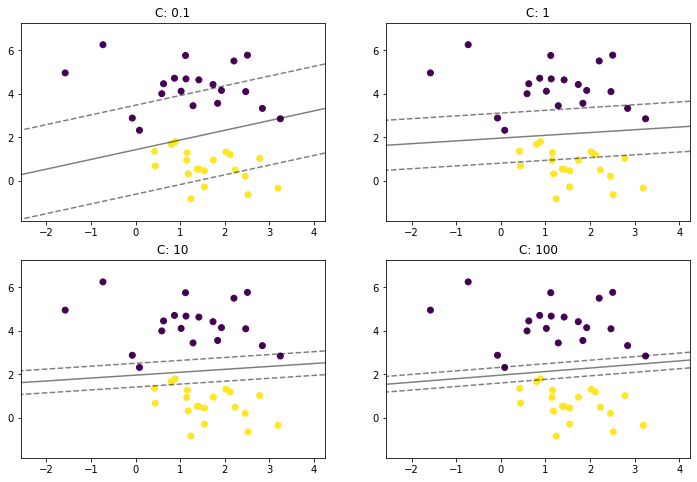
多分类
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
y = iris.target注意SVM中只支持ovr ~
clf = LinearSVC(C = 0.1, multi_class='ovr', random_state=0)
clf.fit(x, y)LinearSVC
LinearSVC(C=0.1, random_state=0)
clf.predict(x)array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
5、非线性SVM —— 核技巧
线性不可分问题
升维映射

高维线性可分

已经有前人在数学上证明:
如果原始的空间是有限的,也就是说特征数是有限的,
那么一定存在一个高位的特征空间能够分割这些样本。

软间隔对偶 dual 问题

则现在就要解决右边的问题。
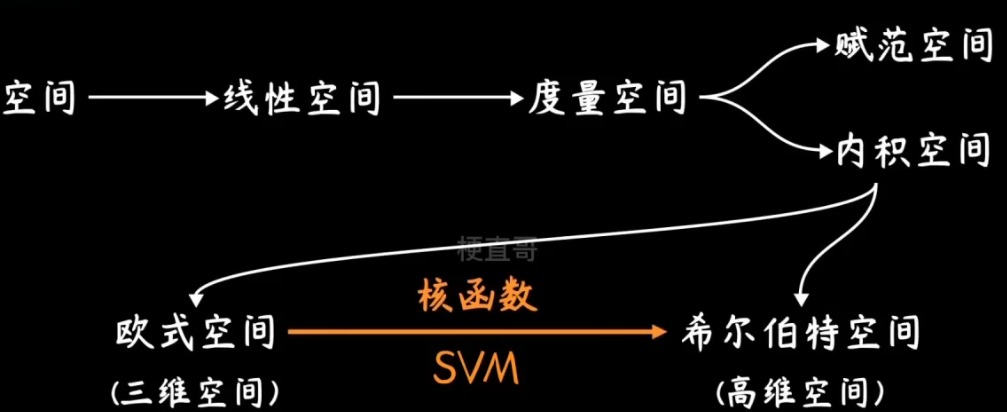
套上一个 φ 就可以升维,但是可能会导致维度灾难,所以就要使用核函数。
【数之道26】SVM支持向量机-核技巧Kernel Trick详解(多项式核函数,无限维度高斯核函数)_哔哩哔哩_bilibili

常用的核函数
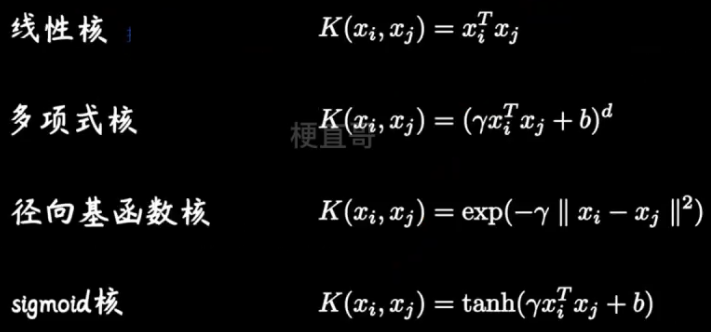
他们就像一个武器套装,能够方便针对软间隔对偶问题实现升维操作。
那么为什么升维就能解决不可分的问题呢?
希尔伯特空间的元素是函数,因此可以看成无穷维度的向量。
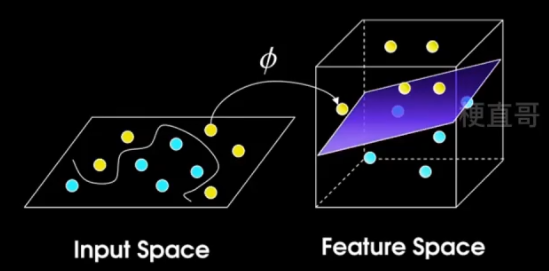
核技巧的作用
映射到高维空间。
大大减少了计算量,尤其是对于高维向量的相乘操作,同时也不需要额外存储中间的结果。
不仅限于SVM,实际上 只要存在着 xi ,xj 的最优化问题。
6、非线性SVM —— 核函数
核函数:是映射关系的内积。
映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数,这通常是我们希望的。
要注意,核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法!
一般英文文献对Kernel有两种提法,一是Kernel Function,二是Kernel Trick。从Trick一词中就可以看出,这只是一种运算技巧而已,不涉及什么高深莫测的东西。
核技巧(kernel trick)的作用,一句话概括的话,就是降低计算的复杂度,甚至把不可能的计算变为可能。
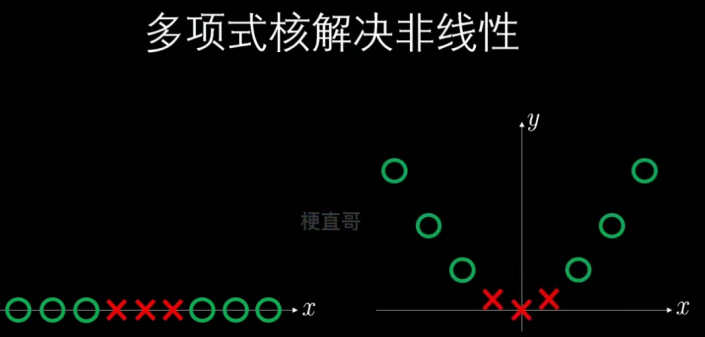
多项式核函数

以下将说明,为什么这个核函数相当于引入了多项式的特征。
为了推导方便,此处使用x,y


高斯核函数

也叫 RBF核函数、径向基函数
Radial Basic Function Kernel

则根据下图可知,当 γ 越大的时候,映射的高斯函数就越发陡峭。

在做高斯核映射时,需要选择地标。也就是下图中公式里的 y。

每个数据点都可以当做地标。
所以有多少个数据就会映射出多少个维度。
假定现在有m个维度为n的数据,则高斯核就可以将其映射成mxm维的数据。
当m非常大的时候,高斯核的运算效率其实很低,但当m并不大甚至小于n的时候,使用核函数就会变得非常高效了。(?存疑 核函数不是升维吗?)
存疑(以下为GPT解答)
在使用高斯核函数进行样本处理时,将维度缩减是一种常见的降维技术。核函数能够将原始样本从n维映射到m维(m < n),从而达到降低样本维度的目的。
为什么在m小于n的情况下仍然要使用核函数呢?这是因为核函数的作用不仅仅是降维,还能够通过非线性映射将样本从原始空间映射到一个更高维的特征空间,从而更好地分离不同类别的样本。即使在降维的过程中,核函数也能够通过引入额外的非线性维度来提高分类性能。
具体来说,当m小于n时,使用核函数的优势在于:
-
非线性映射:核函数通过非线性映射将样本从原始空间映射到一个更高维的特征空间,可以更好地分离不同类别的样本。
-
解决线性不可分问题:在原始空间中,某些样本可能是线性不可分的,但在高维特征空间中可能是线性可分的。通过核函数的映射,可以将原始空间中线性不可分的样本转换为高维特征空间中线性可分的样本,从而提高分类的准确性。
-
计算效率:尽管高斯核在特征空间中引入了更高的维度,但由于核函数的计算与原始样本维度无关,因此计算效率并不受到影响。相反,通过核技巧,我们可以在低维空间中计算高维特征空间的内积,避免了显式地进行高维计算,从而提高了计算效率。
总之,即使在m小于n的情况下,使用核函数仍然能够发挥作用,通过非线性映射和解决线性不可分问题来提高分类性能,并且可以在计算效率上获得一定的优势。
7、非线性SVM代码实现
如何选择核函数?
当特征多且接近样本数量,可直接选择线性核SVM。
当特征数少,样本数正常,推荐选用高斯核函数。
当特征数少,样本数很大,建议选择多项式核函数,切记阶数不能过高,否则复杂度过高,难以计算。
多项式特征解决非线性问题
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.datasets import make_moons
x, y = make_moons(n_samples=100, noise=0.2, random_state=0)
plt.scatter(x[:,0], x[:,1], c = y)
plt.show()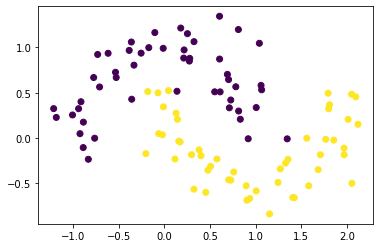
from sklearn.svm import LinearSVC
lsvc = LinearSVC()
lsvc.fit(x,y)LinearSVC
LinearSVC()
def decision_boundary_plot(X, y, clf):
axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
z = z.reshape(x1.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])
plt.contourf(x1, x2, z, cmap=custom_cmap)
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()decision_boundary_plot(x,y,lsvc)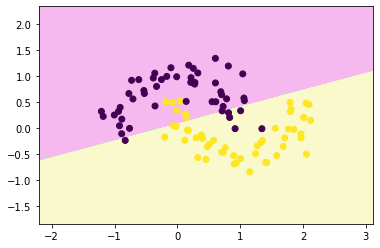
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipelinepoly_svc = Pipeline([
("poly", PolynomialFeatures(degree=3)),
("std_scaler", StandardScaler()),
("linearSVC", LinearSVC())
])poly_svc.fit(x,y)Pipeline
Pipeline(steps=[('poly', PolynomialFeatures(degree=3)),
('std_scaler', StandardScaler()), ('linearSVC', LinearSVC())])
PolynomialFeatures
PolynomialFeatures(degree=3)
StandardScaler
StandardScaler()
LinearSVC
LinearSVC()
decision_boundary_plot(x,y,poly_svc)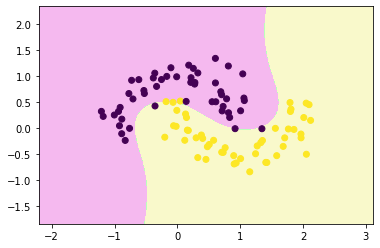
核函数解决非线性问题
from sklearn.svm import SVCpoly_svc = Pipeline([
("std_scaler", StandardScaler()),
("polySVC", SVC(kernel='poly', degree=3, coef0=5 ))
])
poly_svc.fit(x,y)Pipeline
Pipeline(steps=[('std_scaler', StandardScaler()),
('polySVC', SVC(coef0=5, kernel='poly'))])
StandardScaler
StandardScaler()
SVC
SVC(coef0=5, kernel='poly')
decision_boundary_plot(x,y,poly_svc)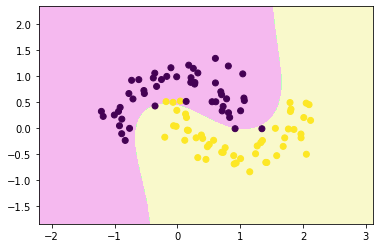
rbf_svc = Pipeline([
("std_scaler", StandardScaler()),
("rbfSVC", SVC(kernel='rbf', gamma=0.1 ))
])
rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)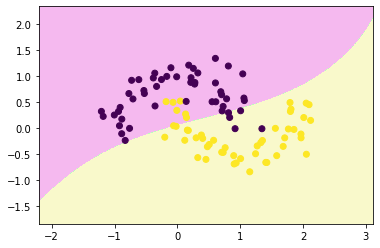
rbf_svc = Pipeline([
("std_scaler", StandardScaler()),
("rbfSVC", SVC(kernel='rbf', gamma=10 ))
])
rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)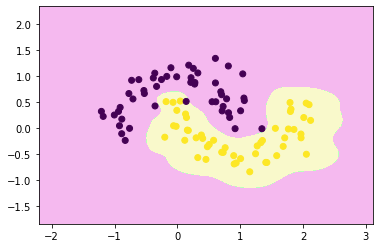
rbf_svc = Pipeline([
("std_scaler", StandardScaler()),
("rbfSVC", SVC(kernel='rbf', gamma=100 ))
])
rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)
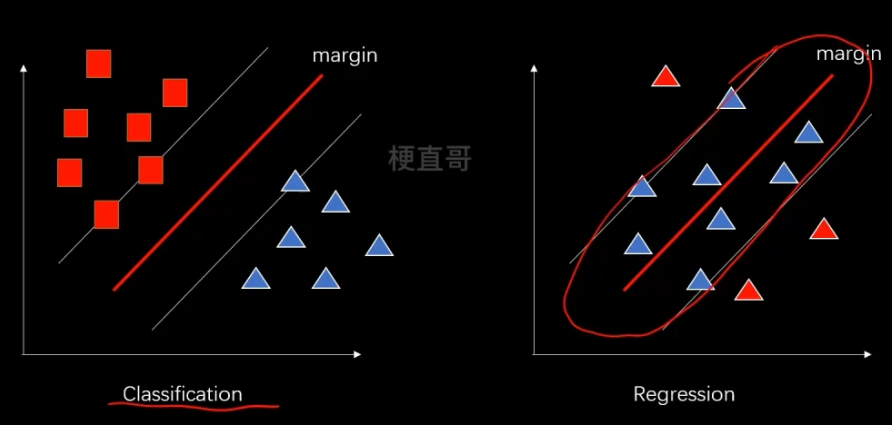
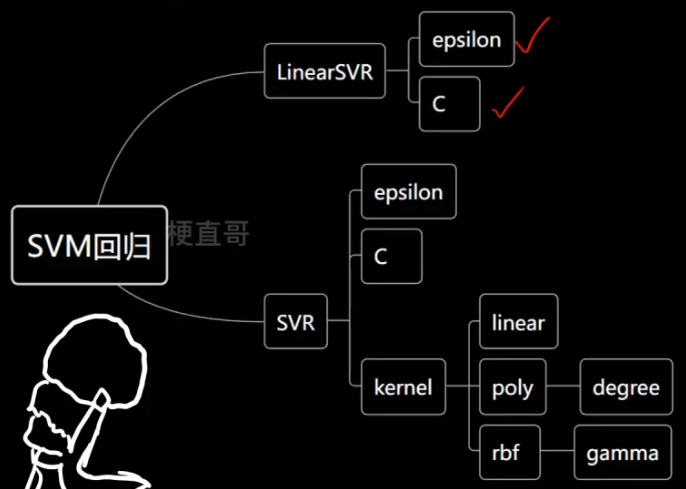
8、SVM解决回归任务

解决回归任务则是希望落在 margin 里的样本点越多越好。
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(666)
x = np.random.uniform(-3,3,size=100)
y = 0.5 * x**2 +x +2 +np.random.normal(0,1,size=100)
X = x.reshape(-1,1)plt.scatter(x,y)
plt.show()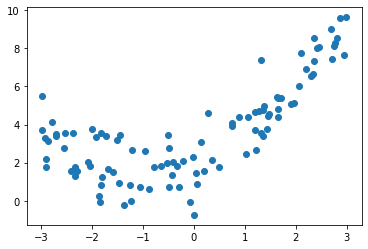
from sklearn.svm import LinearSVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipelinedef StandardLinearSVR(epsilon=0.1):
return Pipeline([
("std_scaler",StandardScaler()),
("linearSVR",LinearSVR(epsilon=epsilon))
])svr = StandardLinearSVR()
svr.fit(X,y)
y_predict = svr.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()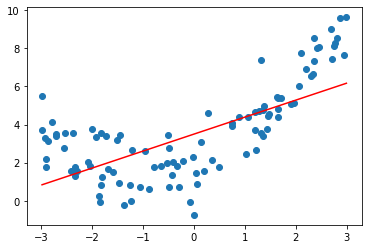
svr.score(X,y)0.48764762540009954
from sklearn.svm import SVRdef StandardSVR(epsilon=0.1):
return Pipeline([
('std_scaler',StandardScaler())
,('SVR',SVR(kernel='rbf',epsilon=epsilon))
])svr = StandardSVR()
svr.fit(X,y)
y_predict = svr.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()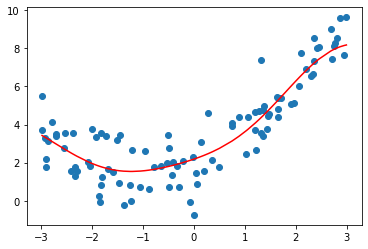
svr.score(X,y)0.8138647789256847
9、SVM的优缺点及适用条件
优点:
1、高效处理非线性数据
2、L2正则化特性,良好的泛化能力
3、解决分类 SVC 和回归 SVR 问题
4、稳定性
缺点:
1、选择合适的核函数比较困难
2、大量内存需求,必须将所有的支持向量都存储在内存中
3、大数据集上训练时间长
4、难以解释
适用条件:小样本数据、非线性数据
参考
核函数 高斯核函数,线性核函数,多项式核函数-CSDN博客
对SVM中核函数的理解_核函数优缺点-CSDN博客


![[计网00] 计算机网络开篇导论](https://img-blog.csdnimg.cn/direct/5406f43cd4dc444e8c89e5ce4cd49a6f.png)