单词搜索 II

news2024/11/24 4:55:49

题目链接

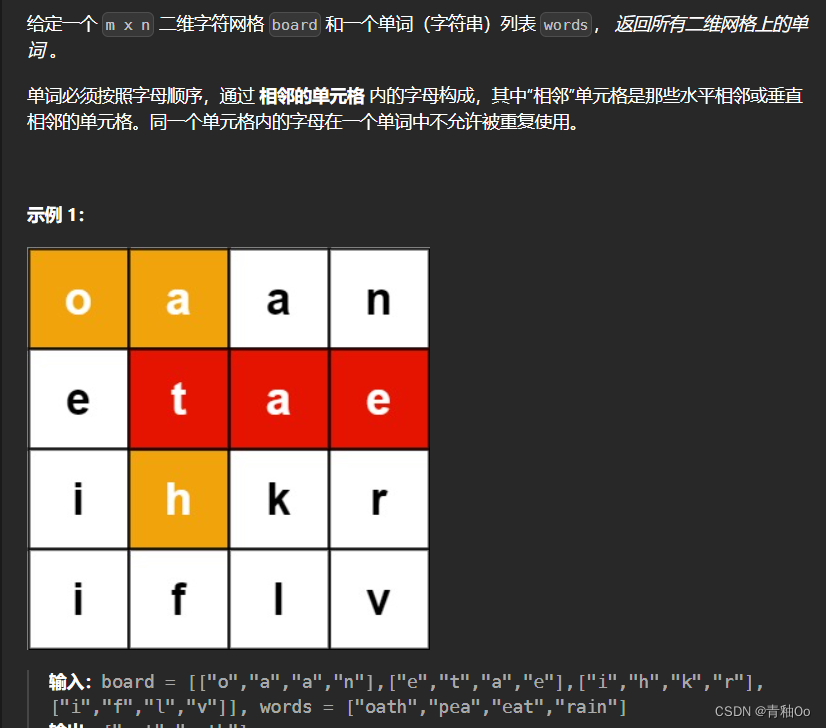
单词搜索 II

题目描述

注意点

board[i][j] 是一个小写英文字母
words[i] 由小写英文字母组成
words 中的所有字符串互不相同
同一个单元格内的字母在一个单词中不允许被重复使用

解答思路

要想找到一个完整的单词，首先想到的是深度优先遍历，如果想要时间复杂度更低，很容易想到剪枝，剪枝的节点在于如果某个字符串在words中没有一个单词的前缀与该字符串重合（注意不是words中不包含该字符串），所以还要用到前缀树的知识，可以参考前缀树，所以本题的主要思路为深度优先遍历+剪枝+前缀树
第一步要完成的是前缀树的构建，因为本题中所有单词都是由小写字母组成，所以前缀树的子树可以由大小为26的TrieNode数组构成；第二步是遍历整个board数组，将任意位置作为起点；第三步是从起点开始深度优先遍历，在搜索单词的期间判断其是否在前缀树中，如果不存在则直接剪枝，如果存在则需要判断其是否是单词并重复进行第三步进行深度优先遍历（注意，在此期间，需要对该位置是否遍历进行回溯）

代码

class Solution {
    public List<String> findWords(char[][] board, String[] words) {
        List<String> res = new ArrayList<>();
        int row = board.length;
        int col = board[0].length;
        // 存储board[i][j]是否已经访问过
        boolean[][] visited = new boolean[row][col];
        // 构建前缀树
        Trie trie = new Trie();
        for (String word : words) {
            trie.insert(word);
        }
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                dfs(board, words, visited, trie.root, res, i, j);
            }
        }
        return res;
    }

    public void dfs(char[][] board, String[] words, boolean[][] visited, TrieNode trieNode, List<String> res, int i, int j) {
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
            return;
        }
        if (visited[i][j]) {
            return;
        }
        trieNode = trieNode.childTrie[board[i][j] - 'a'];
        // 在前缀树中未找到该前缀
        if (trieNode == null) {
            return;
        }
        if (trieNode.word != null && !"".equals(trieNode.word)) {
            res.add(trieNode.word);
            // 该单词已经加入到结果集中，删除防止重复添加
            trieNode.word = null;
        }
        visited[i][j] = true;
        // 上下左右四个方向深度搜索单词
        dfs(board, words, visited, trieNode, res, i - 1, j);
        dfs(board, words, visited, trieNode, res, i + 1, j);
        dfs(board, words, visited, trieNode, res, i, j - 1);
        dfs(board, words, visited, trieNode, res, i, j + 1);
        // 回溯
        visited[i][j] = false;
    }
}

class TrieNode {
    String word;
    TrieNode[] childTrie = new TrieNode[26];
}

class Trie {
    TrieNode root = new TrieNode();
    public void insert(String word) {
        TrieNode currTrie = root;
        for (char c : word.toCharArray()) {
            if (currTrie.childTrie[c - 'a'] == null) {
                currTrie.childTrie[c - 'a'] = new TrieNode();
            }
            currTrie = currTrie.childTrie[c - 'a'];
        }
        currTrie.word = word;
    }
}