62.不同路径

代码随想录

按照动规五部曲来分析：

1确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2确定递推公式

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

3dp数组的初始化

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

所以初始化代码为：

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

4确定遍历顺序

这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

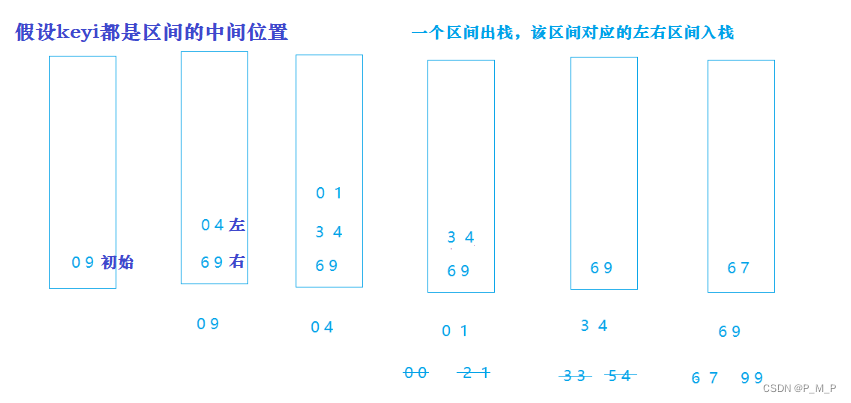
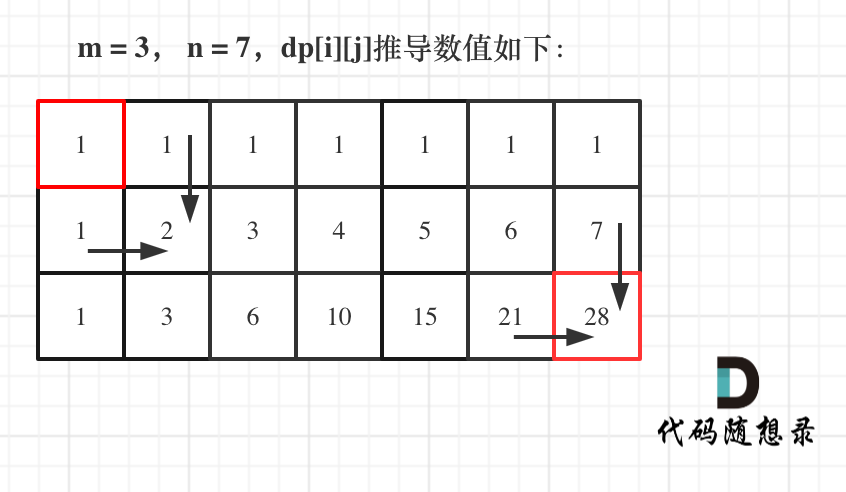
5举例推导dp数组

如图所示：

63. 不同路径 II

初始化有区别：当有障碍，之后的初始化都需要设置为0

dp数组如何初始化

在62.不同路径 (opens new window)不同路径中我们给出如下的初始化：

vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]也同理。

但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。

如图：

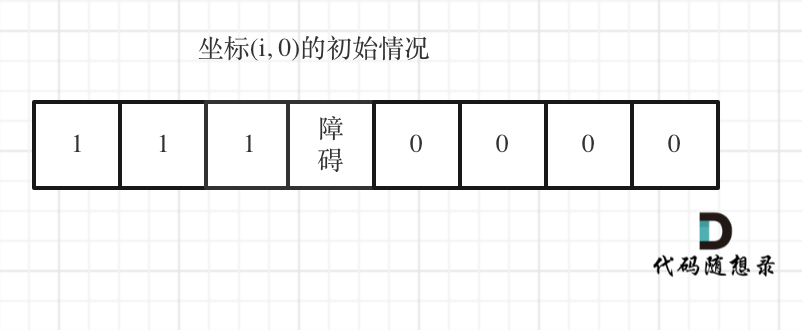
下标(0, j)的初始化情况同理。

所以本题初始化代码为：

vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理

工程能力提升：

直接在循环条件里加上obstacleGrid为0，如果某一个地方为1，直接终止循环，让后面的初始化都为0

        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
            dp[0][j] = 1;
        }

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        //如果在起点或终点出现了障碍，直接返回0
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
            return 0;
        }

        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
            dp[0][j] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
            }
        }
        return dp[m - 1][n - 1];
    }
}