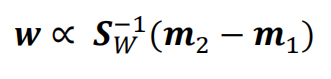Linear classifiers——线性分类器

news2024/12/26 11:46:22

1.(Generalized) Linear classifiers——广义线性分类器

1.1 模型

假如有两类数据，类别标签为y = 1和y = -1

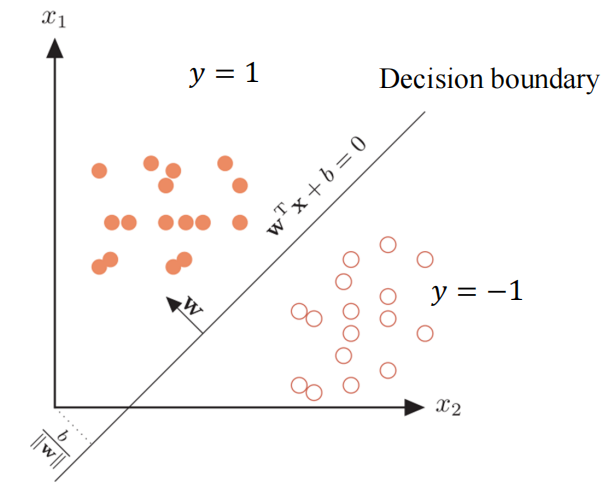
我们可以使用一个线性函数将其分类，二维形式

通常x增加一个恒等于1的维度，可以将b合并进w，于是更一般的形式为

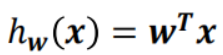
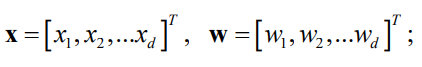
$x_{1}=1$ , $w_{1}$ 就相当于b

输出分类标签

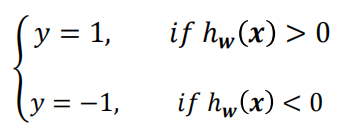
1.2 几何意义

对于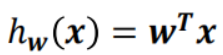，其法向量为 $(w_{1},w_{2},w_{3}\cdots ,w_{n})=W$ ,单位化 $\frac{W}{\left \| W \right \|}$

对于平面上的一个数据点的向量来说，可以被分解为如下

其中表示向量x在决策函数上的投影向量，γ表示x到决策边界的距离，那么就表示x垂直决策边界的向量

由点到面的距离公式可得，x到决策函数的距离

$\gamma =\frac{h_{w}(x)}{||w||}$

变形得

$h_{w}(x)=\gamma||w||$

决策函数的正负了反映数据点的类别，而且其大小也反映了数据点到决策边界距离

2.Fisher’s linear discriminant——Fisher’s 线性判别

1.Fisher’s 线性判别的原理

Fisher’s 线性判别通过降维的方式进行两类别分离，将高纬度的数据在低纬度上进行投影。投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大，也就是“类内小，类间大”。

例有两类数据“x”"o",二维的数据降维就是投影到一条直线上

选取不同的投影轴，会产生不同的效果，很明显第一张图效果就比第二张图好,所以只需要找到一个满足需求的W向量就能实现分类任务。

2.Fisher’s 线性判别的推导

假设投影到w向量上，同时限定|w|=1,拥有两个特征的数据点向量 $x$ 投影到向量w上等于 $w^{\top }x$ (w相当于一个新的坐标轴， $x$ 通过投影在w轴上的获得的值)

证明：

$x_{i}$ 在w上的投影长度为y= $|x_{i}|cos\theta$

$w^{\top }x_{i}=|w||x_{i}|cos\theta=z$

于是我们可以建立

通过1.可知，数据点会分布在w上的不同位置，通过设定一个阈值 $T_{0}$ 完成分类

假设我们有两个类别 $C_{1}$ 和 $C_{2}$ ，分别有 $N_{1}$ 和 $N_{2}$ 个数据

可以计算出两类数据的均值，通过均值的差距来表现类间的差距

${m}_1=\frac{1}{N_1}\sum_{i=1}^{N_1}\mathbf{x}_i=\frac{1}{N_1}\sum_{i=1}^{N_1}w^{\top }{x}_i$ ,

${m}_2=\frac{1}{N_2}\sum_{i=1}^{N_2}\mathbf{x}_i=\frac{1}{N_2}\sum_{i=1}^{N_2}w^{\top }{x}_i$

同样可以计算出两类数据的方差，通过方差来表现类内的差距

$s_1^2=\frac{1}{N_1}\sum_{i=1}^{N_1}(w^{T}x_{i}-{m_1})(w^{T}x_{i}-{m_1})^T$

$s_2^2=\frac{1}{N_2}\sum_{i=1}^{N_2}(w^{T}x_{i}-{m_2})(w^{T}x_{i}-{m_2})^T$

根据“类内小，类间大”的思想，我们可以建立如下目标函数

$J(\mathbf{w})=\frac{(m_1-m_2)^2}{s_1^2+s_2^2}$ ，与类间均值成正比，类内方差成反比

$\begin{aligned} ({m_{1}}-{m_{2}})^{2}& =(\frac1{N_1}\sum_{i=1}^{N_1}w^Tx_i-\frac1{N_2}\sum_{i=1}^{N_2}w^Tx_i)^2 \\ &=(w^T(\frac{1}{N_1}\sum_{i=1}^{N_1}x_i-\frac{1}{N_2}\sum_{i=1}^{N_2}x_i))^2 \\ &=(w^T(\overline{x_1}-\overline{x_2}))^2 \\ &=w^T(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})^Tw \end{aligned}$

$\begin{aligned} s_{1}^2+s_{2}^2& =\frac{1}{N_{1}}\sum_{i=1}^{N_{1}}(w^{T}x_{i}-{m_{1}})(w^{T}x_{i}-{m_{1}})^{T}+\frac{1}{N_{2}}\sum_{i=1}^{N_{2}}(w^{T}x_{i}-{m_{2}})(w^{T}x_{i}-{m_{2}})^{T} \\ &=\frac{1}{N_1}\sum_{i=1}^{N_1}(w^Tx_i-\frac{1}{N_1}\sum_{i=1}^{N_1}w^Tx_i)(w^Tx_i-\frac{1}{N_1}\sum_{i=1}^{N_1}w^Tx_i)^T+\frac{1}{N_2} \\ &\sum_{i=1}^{N_{2}}(w^{T}x_{i}-\frac{1}{N_{2}}\sum_{i=1}^{N_{2}}w^{T}x_{i})(w^{T}x_{i}-\frac{1}{N_{2}}\sum_{i=1}^{N_{2}}w^{T}x_{i})^{T} \\ &=w^T\frac1{N_1}\sum_{i=1}^{N_1}[(x_i-\overline{x_1})(x_i-\overline{x_1})^T]w+w^T\frac1{N_2}\sum_{i=1}^{N_2}[(x_i-\overline{x_2})(x_i-\overline{x_2})^T]w \\ &=w^Ts_{1}^2w+w^Ts_{2}^2w \\ &=w^{T}(s_{1}^2+s_{2}^2)w \end{aligned}$