代码随想录算法训练营第十三天（栈与队列）| 239. 滑动窗口最大值，347.前 K 个高频元素

239. 滑动窗口最大值

之前讲的都是栈的应用，这次该是队列的应用了。

本题算比较有难度的，需要自己去构造单调队列，建议先看视频来理解。

题目链接/文章讲解/视频讲解：
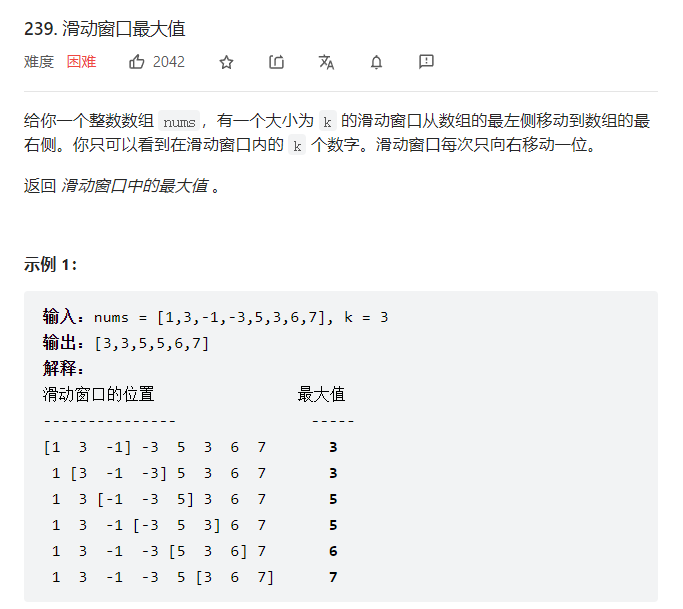
在这里插入图片描述

看到题目的第一想法：

想了半天没想出来，就直接看卡哥的题解了。

看完代码随想录之后的想法：

构造一个单调队列，这个队列没有必要维护窗口的所有元素，只需要维护可能成为窗口最大值的元素就可以了，同时保证元素的数值是由大到小的。

package com.second.day13;

import java.util.Deque;
import java.util.LinkedList;

public class MyQueue {
    Deque<Integer> queue = new LinkedList<>();

    public void pop(int value) {
        if(!queue.isEmpty() && queue.peek() == value) {
            queue.poll();
        }
    }

    public void push(int value) {
        while(!queue.isEmpty() && queue.getLast() < value) {
            queue.removeLast();
        }
        queue.offer(value);
    }

    public int getMax() {
        return queue.peek();
    }
}

package com.second.day13;

public class MaxSlidingWindow_239 {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] result = new int[nums.length - k + 1];
        MyQueue queue = new MyQueue();
        for(int i = 0; i < k; i++) {
            queue.push(nums[i]);
        }
        result[0] = queue.getMax();
        int index = 1;
        for(int i = k; i < nums.length; i++) {
            queue.pop(nums[i - k]);
            queue.push(nums[i]);
            result[index++] = queue.getMax();
        }
        return result;
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1,3,1,2,0,5};
        MaxSlidingWindow_239 demo = new MaxSlidingWindow_239();
        for (int i : demo.maxSlidingWindow(nums, 3)) {
            System.out.print(i + " ");
        }
    }
}

自己实现过程中遇到哪些困难：

无

347. 前 K 个高频元素

大/小顶堆的应用，在C++中就是优先级队列

本题是大数据中取前k值的经典思路，了解想法之后，不算难。

题目链接/文章讲解/视频讲解：

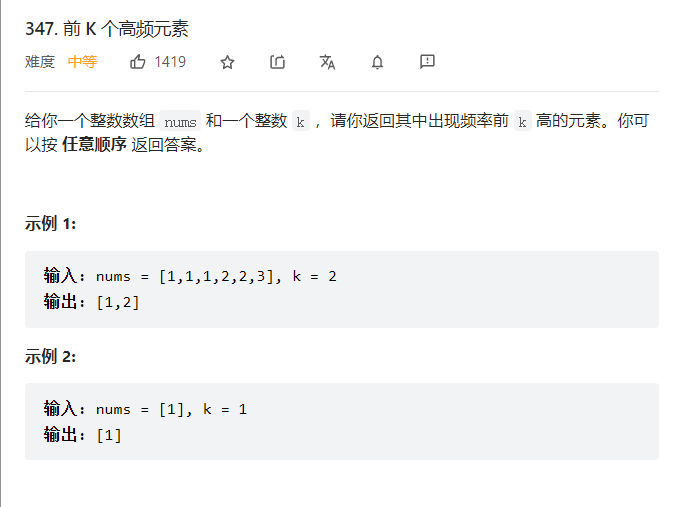
在这里插入图片描述

看到题目的第一想法：

1.用map记入各个数出现的个数
2.对map进行排序
3.输出前k多的数
但是不知道怎么实现。

看完代码随想录之后的想法：

对map进行排序使用优先队列。

package com.second.day13;

import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;

public class TopKFrequent_347 {
    public int[] topKFrequent(int[] nums, int k) {
        //1.构造一个map，统计各个数出现的次数
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //2.构造一个大顶堆
        //在优先队列PriorityQueue中存储(num, cnt)，cnt表示元素值num在数组中出现的次数
        //出现的次数在队列中是按从小到大的顺序进行排序的
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()) {
            pq.add(new int[]{entry.getKey(), entry.getValue()});
        }
        //3.取出大顶堆前k个数
        int[] result = new int[k];
        for(int i = 0; i < k; i++) {
            result[i] = pq.poll()[0];
        }
        return result;
    }
}