文章目录
- 1. 不同路径
- 题干:
- 算法原理:
- 代码:
- 2. 二分查找
- 题干:
- 算法原理:
- 1、暴力解法 O(n)
- 2、二分查找算法
- 朴素二分模版:
- 代码:
1. 不同路径


原题链接
题干:
机器人只能向下和向右走,不能回退(向上或者向左)
算法原理:
- 状态表示
经验 + 题目要求
以[ i,j ] 为结尾时…
dp[i][j] 表示:走到 [i, j] 位置处,⼀共有多少种方式 - 状态转移方程
最近的一步 划分问题
因为只能从上面或者左边走到这个位置
所以
从 [i, j] 位置的上方( [i - 1, j] 的位置)向下走一步,转移到 [i, j] 位置
从 [i, j] 位置的左方( [i, j - 1] 的位置)向右走⼀步,转移到 [i, j] 位置

不过,这里走的是一步,而不是一次
所以并不是上一步+1,而是直接加上下一步可能得次数
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - 初始化
这里我们依然要使用虚拟节点来写
不过,这里我们要做到以下两点:
(1)虚拟节点里面的值,要保证后面填表的结果正确
(2)下标的映射
这里最重要的就是第一点
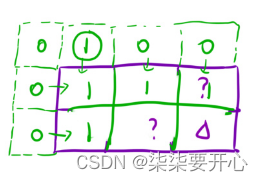
在这里,因为求的第一行的值都是 1
这里就需要第一行第一列上面的虚拟节点为 1 - 填表顺序
从上往下填写每一行
每一行从左往右填写 - 返回值
dp[m][n]
代码:
class Solution {
public int uniquePaths(int m, int n) {
//1.创建dp 表
//2.初始化
//3.填表
//4.返回值
int[][] dp = new int [m + 1][n + 1];
dp[0][1] = 1;
for(int i = 1; i <= m; i ++) {//从上往下每一行
for(int j = 1; j <= n; j++) {//从左往右填写每一行
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}
2. 二分查找

原题链接
题干:
n 个元素有序的数组,找到 target,返回下标
算法原理:
1、暴力解法 O(n)
从头开始遍历,遇到 target 返回
2、二分查找算法
使用“二分查找”,在遇到“二段性”的时候可用
在一个数组中,拿到目标值 在数组中查找,发现可以划分为两端的区域
并且可以选择性的舍去一段,在另一段进行查找
这个时候就可以使用
(二分查找并不一定在有序数组,满足“二段性”就可用)
- 定义 left ,right 指针,分别指向数组的左右区间
- 找到待查找区间的中间点 mid ,找到之后分三种情况讨论:
(1)arr[mid] == target 说明正好找到,返回 mid 的值
(2)arr[mid] > target 说明 [mid, right] 这段区间都是⼤于 target 的,因此舍去右边区间,在左边 [left, mid -1] 的区间继续查找,即让 right = mid -1 ,然后重复 2 过程
(3)arr[mid] < target 说明 [left, mid] 这段区间的值都是⼩于 target 的,因此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid +1 ,然后重复 2 过程 - 当 left 与 right 开时,说明整个区间都没有这个数,返回 -1
看图也可
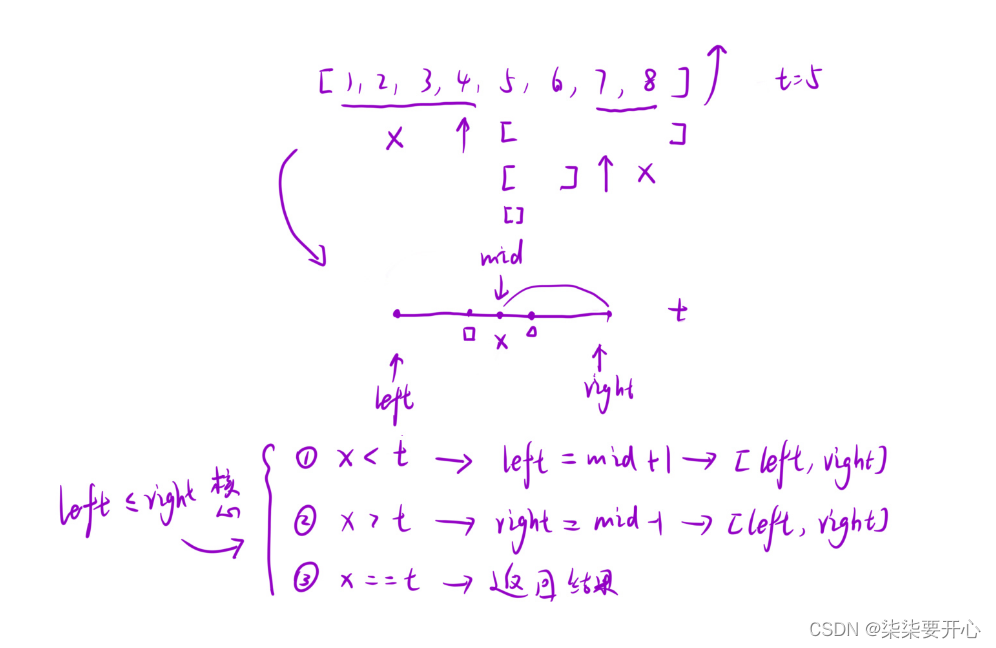
细节问题:
- 循环结束的条件
left > right - 为什么是正确的
虽然比较的次数少,但是与暴力解法相似,因此结果是正确的 - 时间复杂度
long(n)
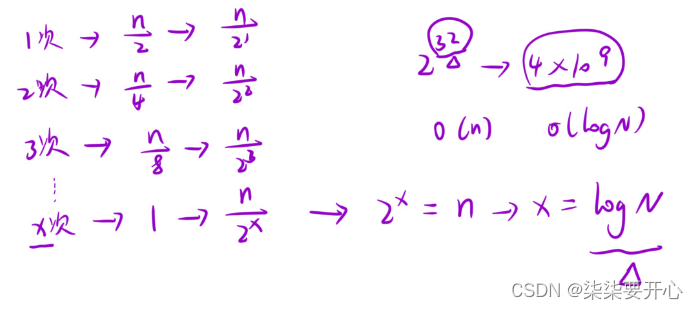
朴素二分模版:
while(left <= right) {
int mid = left + (right - left) / 2;//防止溢出
if(......) {
left = mid + 1;
}else if(......) {
right = mid - 1;
}else{
return ......;
}
}
代码:
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;//为了防止溢出问题
if(nums[mid] < target) {
left = mid + 1;
}else if(nums[mid] > target) {
right = mid - 1;
}else{
return mid;
}
}
return -1;
}
}