1.题目描述

给定一个非负整数numRows，生成杨辉三角的前numRows行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

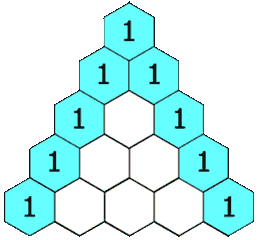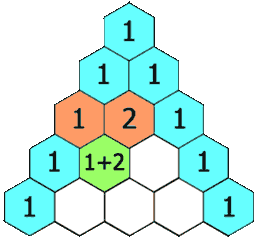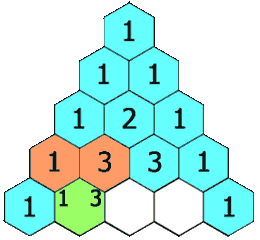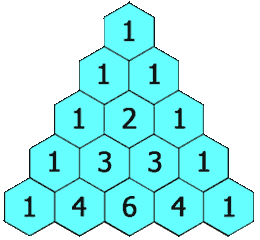
示例1

输入：numRows = 5

输出：[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]

示例2

输入：numRows = 1

输出：[1]

提示：

• 1 <= numRosw <= 30

2. 解题思路

1. 生成一个二维数组，三角形的每一行都以一维数组的形式存储。
2. 三角形的每一行的第一个数字和最后一个数字都是1。
3. 每一个三角的元素等于上一行此位置左边的元素与上一行此位置元素的和。
4. 将本行结果加入三角

3.代码

class Solution {
    public List<List<Integer>> generate(int numRows) {
        // 定义一个二维数组用于存储生成的杨辉三角
        List<List<Integer>> ret = new ArrayList<>();
        
        // 定义一个一维数组用于存储每一行的元素
        List<Integer> list = new ArrayList<>();
        list.add(1); // 第一行只有一个元素1
        ret.add(list); // 将第一行添加到二维数组中
        
        // 循环生成每一行的元素
        for (int i = 1; i < numRows; i++) {
            // 定义一个一维数组用于存储当前行的元素
            List<Integer> curRow = new ArrayList<>();
            curRow.add(1); // 每一行的第一个元素都为1
            
            // 处理中间的元素
            List<Integer> prevRow = ret.get(i - 1); // 获取上一行的元素
            for (int j = 1; j < i; j++) {
                // 当前元素等于上一行的当前位置元素和前一个位置元素的和
                int x = prevRow.get(j) + prevRow.get(j - 1);
                curRow.add(x); // 将当前元素添加到当前行中
            }
            
            curRow.add(1); // 每一行的最后一个元素都为1
            ret.add(curRow); // 将当前行添加到二维数组中
        }
        
        return ret; // 返回生成的杨辉三角
    }
}

运行结果：

4. 复杂度分析

• 时间复杂度：O(numRows²)，因为计算总数为 1 + 2 + 3 + …+ numRows。
• 空间复杂度：O(numRows²)，因为每次计算都会被保留下来，因此空间复杂度的规模与时间复杂度相同。