Leetcode 51 N 皇后

news2024/9/28 17:26:52

题意理解：

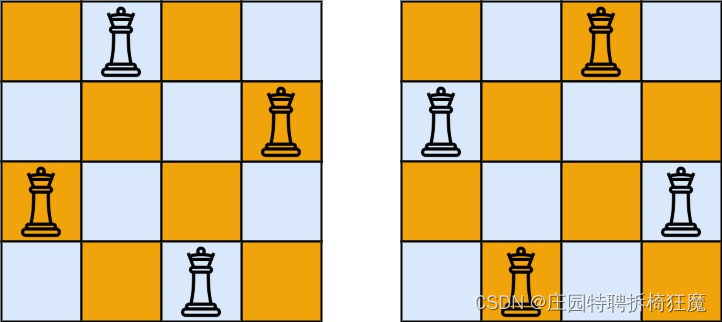
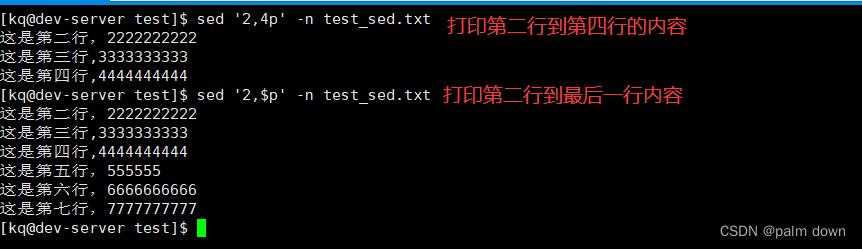
N皇后问题指的是在一个n×n的棋盘上，防止皇后棋子，每行、每列、每45°斜角只能有一个皇后存在。

这是一道困难的题：困难在于：

如何处理棋盘，如何表示棋子。

将期盼看作是2维数组，一行一行来防止合适的棋子，似乎就好理解一些了。

‘.’表示棋子，‘Q’表示皇后

图摘自《代码随想录》

解题思路：

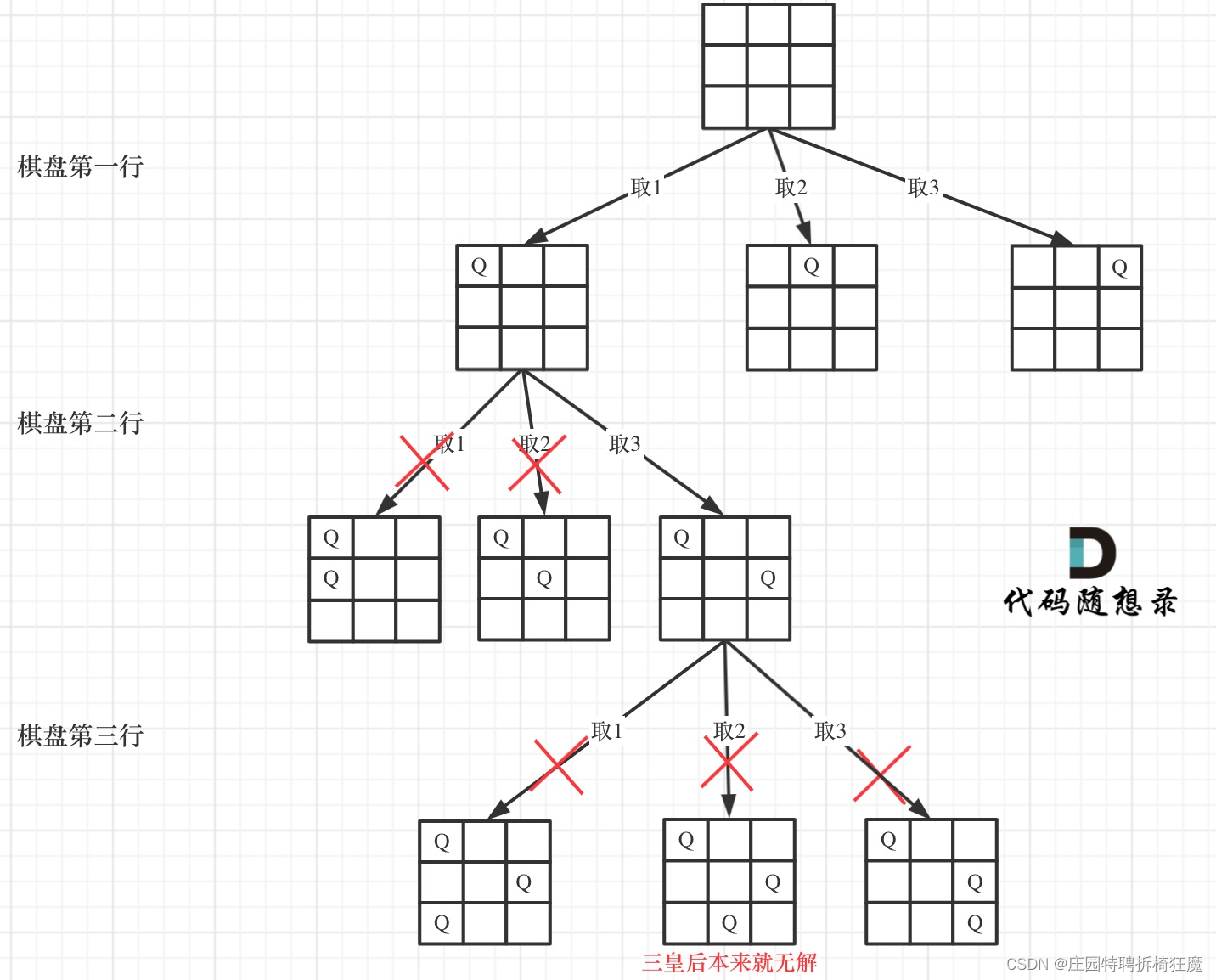
将其棋盘看作一个二维数组，‘.’表示棋子，‘Q’表示皇后。我们使用回溯算法来查找结果集。将其抽象为一棵树结构。

树深=棋盘行数树宽=棋盘列数

用树深遍历行，树宽遍历Q可以取得位置——>目标是找到所有符合的结果。

图摘自《代码随想录》

1.暴力回溯+剪枝优化

前提条件，判断当前位置是否合法的，即是否能合法的放置一个皇后。

回溯的三个关键步骤：

确定返回值和参数列表

确定终止条件：只有符合条件的放置才能放到最后一行，所以，当n=rowIndex时，终止。

确定单层递归逻辑

List<List<String>> result=new ArrayList<>();

    char[][] chessboard=null;
    public List<List<String>> solveNQueens(int n) {
        chessboard=new char[n][n];
        for(char[] row:chessboard)  Arrays.fill(row,'.');
        backtracking(n,0);
        return result;
    }

    public void backtracking(int n,int rowIndex){
        //终止条件
        if(rowIndex==n){
            //收集结果并返回
            result.add(char2List(chessboard));
            return;
        }
        //当前行
        //单层逻辑
        for(int j=0;j<n;j++){
            //该位置是否能合法放置皇后，不合法则剪枝
            if(isValid(chessboard,rowIndex,j)) {
                //合法放皇后
                chessboard[rowIndex][j]='Q';
                backtracking(n,rowIndex+1);
                chessboard[rowIndex][j]='.';
            }
        }
    }

    //判断位置是否合法
    public boolean isValid(char[][] chessboard,int i,int j){
        //放置到第i层时，i+1层还没放
        int leftIndex=j;//左->右斜角检查
        int rightInndex=j;//右->左斜角检查
        while(i>0){
            i--;
            leftIndex--;
            rightInndex++;
            //列检查
            if(i>=0&&chessboard[i][j]=='Q') return false;
            //左->右斜角检查
            if(leftIndex>=0&&chessboard[i][leftIndex]=='Q') return false;
            //右->左斜角检查
            if(rightInndex<chessboard.length&&chessboard[i][rightInndex]=='Q') return false;
        }
        return true;
    }

    public List<String> char2List(char[][] chessboard){
        List<String> result=new ArrayList<>();
        for(char[] row:chessboard)
            result.add(new String(row));
        return result;
    }