概述

现今技术日新月异, Artificial Intelligence 的发展正在迅速的改变我们的生活和工作方式. 尤其是在自然语言处理 (Natural Linguistic Processing) 和计算机视觉 (Computer Vision) 等领域.

传统的多模态对话研究主要集中在单一用户与系统之间的交互, 而忽视了多用户场景的复杂性. 视觉信息 (Visual Info) 往往会被边缘化, 仅作为维嘉信息而非对话的核心部分. 在实际应用中, 算法需要 “观察” 并与多个用户的交互, 这些用户有可能不是当前的发言人.

【CCF BDCI 2023】多模态多方对话场景下的发言人识别, 核心思想是通过多轮连续对话的内容和每轮对应的帧, 以及对应的人脸 bbox 和 name label, 从每轮对话中识别出发言人 (speaker).

Baseline 的代码分为三个文件, 分别为convex_optimization.py, dialog_roberta-constrasive.py, finetune_cnn-multiturn.py. 下面小白我就来带大家详解一下 Solver 部分.

Solver 在多模态发言人识别中的作用

求解器 (Solver) 在多模态发言人识别中的作用是整合和分析来自不同模态的数据, 如食品中的视觉信息和剧本中的文本信息. Slover 的任务是从这些复杂的数据中提取有用的信息, 并最终确定每个对话中的发言人 (Speaker).

Solver 在多模态发言人识别中的重要性

求解器的三大要点:

1. 整合多模态数据: Solver 能够处理来自不同源的数据, 在这个赛题中为 CNN 和 NLP 的输出, 为识别提供不同的视角
2. 优化决策过程: 通过应用数学和统计的方法, Solver 能够在众多潜在的发言人 (Potential) 中找到最优解
3. 提高准确性:相比单一模态分析 (CNN or NLP or Audio, Solver 可以综合考虑多种信息, 先出提高发言人识别的准确率 (可以理解为类似 Bagging 算法)

Solver 的工作原理

Solver 通常采用数字优化技术, 如这次用到的二次规划 (Quadratic Programming), 来解决发言人识别问题. 首先将两个模型的输出转化为数学问题中的参数, 然后用过优化算法寻找这些参数的最优组合, 从而确定发言人 (Speaker).

二次规划

首先声明一下, 小白我是小学毕业, 数学水平停留在2x + 1 = 5的阶段, 下面的内容是基于网上内容 + 我的粗浅理解, 有不对的地方希望大家指正.

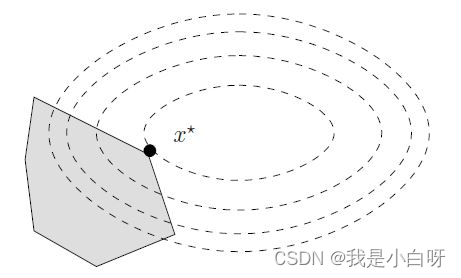
二次规划 (Quadratic Programming). 是一种特殊类型的数学优化问题, 涉及到一个二次目标函数和一系列线性约束.

二次规划的基本形式

二次规划问题可以形式化为下面的数学模型:

• 目标函数: $f(x)=\frac{1}{2}{x}^{T}Qx+c^{T}x$
• 约束条件: $Ax\le b$

其中, $x$ 是需要优化的变量向量, $Q$ 是一个堆成矩阵, $c$ 是一个向量, $A$ 是一个矩阵, $b$ 是一个向量. 目标是找到 $x$ 的值, 使得目标函数 $f(x)$最大或最小化, 同时满足所有的线性约束条件.

二次规划的特点

二次规划的特点:

1. 目标函数的二次性: 二次规划的核心特点是其目标函数是变量的二次函数. 这意味着目标函数可以有一个独特的最大值或最小值, 取决于矩阵 Q 的性质.
2. 线性约束: 尽管目标函数是二次的, 但所有的约束都是线性的. 这些约束定义了一个可行域, 优化必须在这个域内
3. 凸性: 如果矩阵 $Q$ 是半正定的, 哪儿二次规划问题是凸的. 凸二次规划保证了全局最优解的存在

二次规划在多模态发言中的应用 (我的理解)

在多模态发言人识别 (MMSI) 的上下文中, 二次规划 (Quadratic Programming) 用于整合来自不同模型 (CNN & Roberta) 的信息, 并找到最佳的发言人分配方案.

这里的目标函数通常包括两部分:

1. 基于视觉信息, CNN 输出
2. 基于文本信息, Roberta 输出

通过优化这个组合目标函数, Solver 能够在满足一定约束条件的情况下, 分配最可能的发言人 (Speaker).

代码详解

主要步骤:

1. 数据转化: 用与将 CNN 和 Roberta / Deberta 的模型输出转化为优化问题所需的格式
2. 目标函数和约束的设定
3. 优化问题的求解: 通过 Gurobi 求解器求解
4. 优化过程: 确保只有一个发言人被选中
5. 获取结果

数据转化

def convert_cnn_preds_to_matrix(frame_names_list, cnn_scores, label='pred'):
    matrix_list, mappings_list = [], []
    for frame_names in frame_names_list:
        scores = [cnn_scores.get(frame_name, {}) for frame_name in frame_names]
        speakers = set(sum([list(i.keys()) for i in scores], list()))
        speaker_id_mappings = {speaker: i for i, speaker in enumerate(speakers)}
        matrix = np.zeros((len(frame_names), len(speakers)))
        for i, score_dict in enumerate(scores):
            for speaker, score in score_dict.items():
                matrix[i][speaker_id_mappings[speaker]] = score[label]
        matrix_list.append(matrix)
        mappings_list.append(speaker_id_mappings)
    return matrix_list, mappings_list

• 输入: frame_names_list (帧名) 和 cnn_scores (CNN 预测分数)
• 映射: 将每个帧中出现的发言人分配一个索引, 映射到speaker_id_mappings
• 构建矩阵: 对于每个对话, 初始化一个全 0 矩阵, 行等于帧数, 列等于发言人数量. 遍历每个帧的 score, 根据映射将 speaker 对应的分数放到矩阵对应的位置
• 输出:
  • 矩阵列表: 每个对话准话后的矩阵
  • 映射列表: 每个对话 speaker 到索引的映射

目标函数和约束设定

def solve(cnn_scores, roberta_scores):
    '''
    cnn_scores: matrix of shape [n, m]
    roberta_scores: matrix of shape [n, n]
    where m = num_speakers, n = num_sents
    '''

    n, m = cnn_scores.shape
    x = cp.Variable(np.prod(cnn_scores.shape), boolean=True)
    constraints = []
    for i in range(n):
        constraints.append(cp.sum(x[i*m: i*m+m]) == 1)

    cnn_objective = cnn_scores.reshape(-1).T @ x.T
    new_roberta_scores = np.zeros((n*m, n*m))
    for i in range(n):
        for j in range(n):
            for k in range(m):
                new_roberta_scores[i*m+k, j*m+k] += roberta_scores[i, j]

    roberta_objecive = cp.quad_form(x, new_roberta_scores) * (1/2)
    objective = cnn_objective + roberta_objecive

    problem = cp.Problem(cp.Maximize(objective), constraints)
    problem.solve(solver='GUROBI')
    return x.value.reshape(n, m), problem.status

• 变量定义: 定义决策变量x, 是一个布尔型变量的数组, 其余长度等于cnn_scores矩阵的元素总数. 这个变量代表了每个句子选择每个发言人的决策
• CNN 目标函数: cnn_objective是通过将cnn_scores矩阵展平鱼决策变量x的专职相乘得到的. 这部分代表了选择特定发言人的奖励
• Roberta 目标函数:
  • new_roberta_scores: $n\ast m\times n\ast m$, 该矩阵是对roberta_scores的扩展, 用于表示不同句子之间的相似度
  • roberta_objective是通过对决策变量x应用二次形式得到的, 代表了选择相同发言人的奖励
• 总目标函数: 最终的目标函数objective是和cnn_objective和roberta_objextive的和. 这个函数代表了在满足约束条件的前提下, 我们希望最大化的总奖励

约束条件的设定

constraints = []
for i in range(n):
    constraints.append(cp.sum(x[i*m: i*m+m]) == 1)

约束定义: 对于每个句子 (共n个), 添加一个约束条件, 确保每个句子只能选择一个发言人. 具体实现为:

1. 初始化约束李彪: 创建一个空列表constraints, 用于存储所有的约束条件
2. 循环添加约束: 对于每个句子for i in range(n), 执行以下操作:
   • x[i*m: i*m+m]: 是对决策变量x的一个切片操作, 选取与第i个句子相关的部分. 由于x是一个一维数组, 这个切片实际上选取了第i. 即每个句子只能选择一个发言人
3. 添加到约束列表: 将每个句子的约束条件添加到constraints列表中

CVXPY 和 Gurobi 求解

CVXPY

CVXPY 是 Python 的一个库, 用于构建和求解凸优化问题. 在多模态发言人识别的求解器中, CVXPY 被用来定义二次规划问题. 包括构建目标函数 (RNN 输出 + Roberta 输出), 以及定义约束条件 (一个发言人).

Gurobi

Gurobi 是一个强大的数学优化求解器, 广泛应用于工业和学术界和学术界. Gurobi 能够高效的求解各种类型的优化问题. 包括线性规划, 整数规划, 二次规划等. 在我们的 Solver 中, Gurobi 被用作 CVXPY 的后端求解器. 一单优化问题在 CVXPY 中被定义, Gurobi 就被用来实际求解这个问题, 找到最优解.

CVXPY 和 Gurobi 求解优化问题

定义决策变量:

x = cp.Variable(np.prod(cnn_scores.shape), boolean=True)

构建目标函数和约束:

• 上面说过了

创建优化问题:

problem = cp.Problem(cp.Maximize(objective), constraints)

求解优化问题:

problem.solve(solver='GUROBI')

处理求解结果:

return x.value.reshape(n, m), problem.status

Citation

Beasley, J. E. (1998). Heuristic algorithms for the unconstrained binary quadratic programming problem. ResearchGate. Retrieved from https://www.researchgate.net/publication/2661228

Vanderbei, R. J. (1999). LOQO: An interior point code for quadratic programming. Optimization Methods and Software, 11(1-4), 451-484. https://doi.org/10.1080/10556789908805759

Axehill, D. (2008). Integer quadratic programming for control and communication. DIVA. Retrieved from https://www.diva-portal.org/smash/record.jsf?pid=diva2:17358