本题刚接触时比较懵,做出来后就很好理解。之前数据结构的题:给出中序与后序(或前序与中序)画出该树 无从下笔不知如何去画,做完此题后就发现豁然开朗,不过尔尔。本题只讲中序与后序(前序与中序一样的思路和解法)
题目:
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
思路(借鉴了代码随想录):
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:
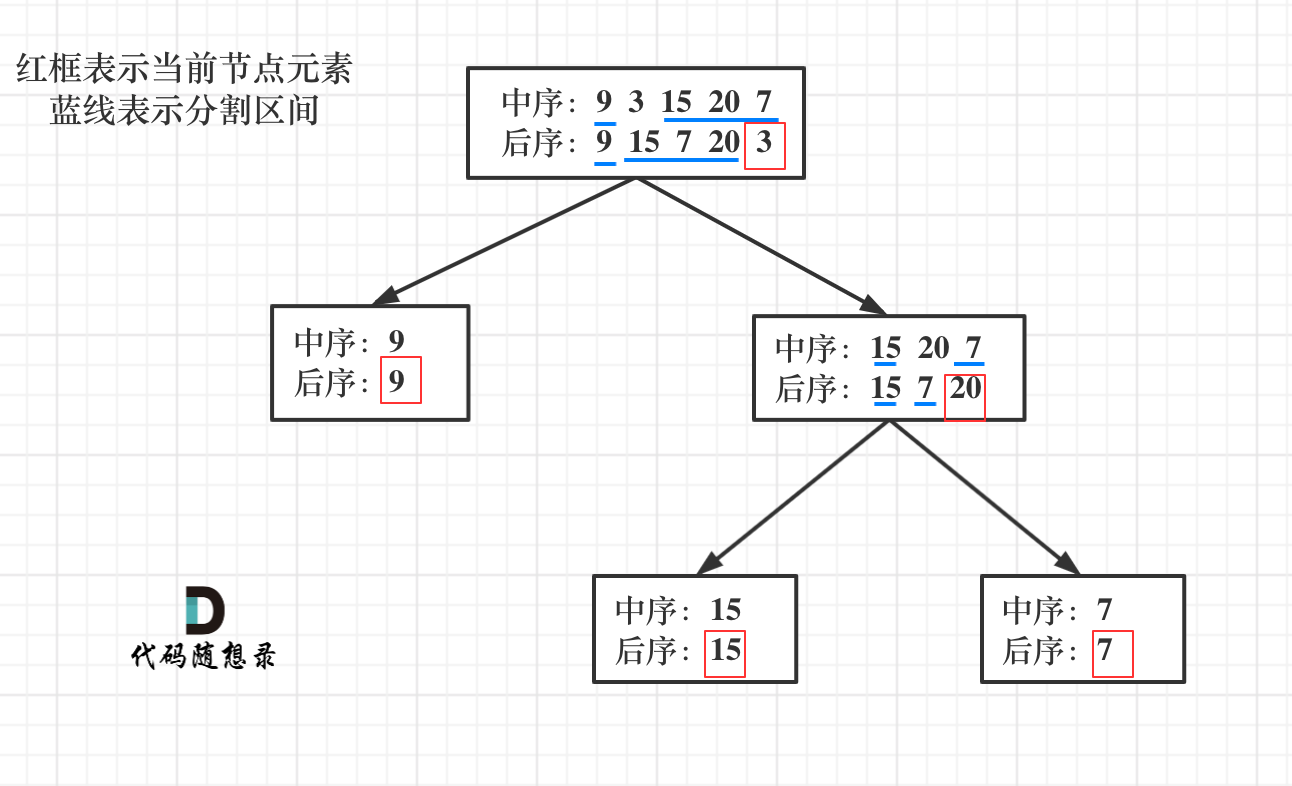
那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
那么如何切割呢:
首先要切割区间,这里全部采用的是同一种切割方式(本题我用的是左闭右开),切割中序数组很简单,那后序数组如何切割呢?
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
代码:
106.从中序与后序遍历序列构造二叉树
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
if not postorder:
return None
# 第二步: 后序遍历的最后一个就是当前的中间节点.
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
postorder_left = postorder[:len(inorder_left)]
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
# 第六步: 递归
root.left = self.buildTree(inorder_left, postorder_left)
root.right = self.buildTree(inorder_right, postorder_right)
# 第七步: 返回答案
return root105.从前序与中序遍历序列构造二叉树
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not preorder:
return None
# 第二步: 前序遍历的第一个就是当前的中间节点.
root_val = preorder[0]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
preorder_left = preorder[1:1 + len(inorder_left)]
preorder_right = preorder[1 + len(inorder_left):]
# 第六步: 递归
root.left = self.buildTree(preorder_left, inorder_left)
root.right = self.buildTree(preorder_right, inorder_right)
# 第七步: 返回答案
return root