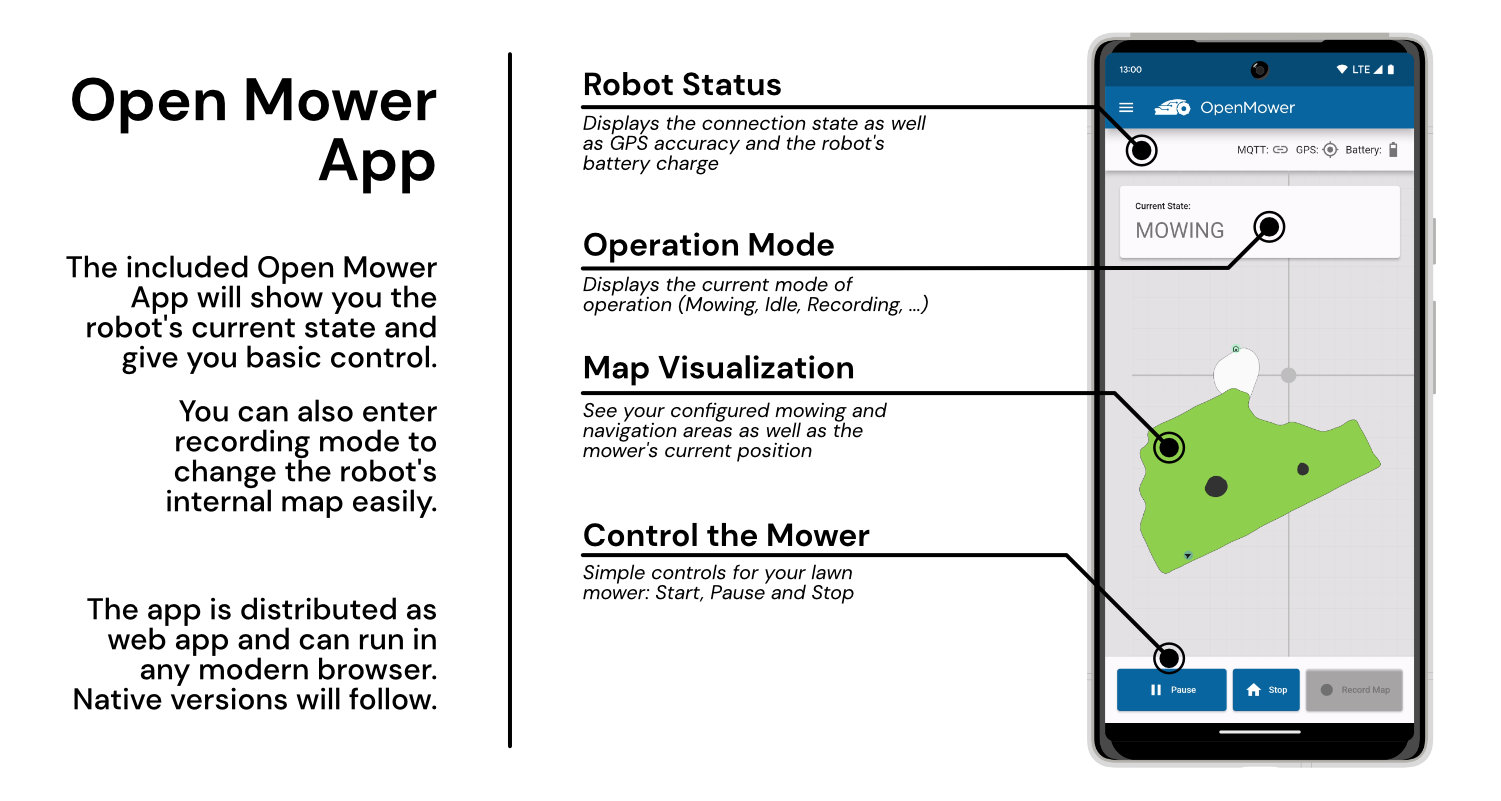
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] result=new int[2];
result[0]=result[1]=-1;
//排除特殊情况
if(nums==null||nums.length==0){
return result;
}
//查找左边界
int left=0;int right=nums.length-1;
while (left<right){
int mid=left+(right-left)/2;
if(nums[mid]<target){
left=mid+1;
}else {
right=mid;
}
}
//left==right,得到最终结果
if(nums[left]!=target){
return result;
}else {
//得到了左边界
result[0]=left;
}
//查找右边界
left=0;right=nums.length-1;
while (left<right){
int mid=left+(right-left+1)/2;
if(nums[mid]<=target){
left=mid;
}else {
right=mid-1;
}
}
//因为查找左边界成功,所以查找右边界就一定成功
result[1]=left;
return result;
}
}
题解:
这是一道经典的二分法解决的问题,代码很简单,但是其中涉及到很多的细节,一不留神就会写出死循环的代码,现在来和小林一起探讨一下
对于一道题是否能够使用二分法,我们需要看题目是否具有二义性,就是说,我们是否能够通过一个条件剔除掉一部分数据,保留另一部分
我们用示例 1 来举例,输入:nums = [5,7,7,8,8,10], target = 8
此时我们想要获取 8 这个数据的起始位置(左边界),我们可以将数组划分为两个部分【5,7,7】【8,8,10】,【5,7,7】的部分是< target 的,【8,8,10】的部分是 >= target 的,我们选取中点 mid = 7 ,7 在 < targe部分,所以 mid 指向的数据肯定不是左边界,于是让 L 指针指向 mid+1 的位置
5 7 7 8 8 10
L mid R
我们再取此时 L 和 R 指针中间的数据 mid = 8,当 mid 在 >= target 的区间时,我们要找的左边界就在这个区间,所以我们不能确定 mid 是否刚好指在我们要寻找的左边界上,但可以排除掉 mid 右边的数据,所以我们让 R 指针指向 mid 的位置
5 7 7 8 8 10
L R
mid
我们再取 L 和 R 指针中间的数据,mid = 8 在 >= target 的区间,所以一样让 R 指针指向 mid 的位置,当 L 和 R 指针相遇时,我们便得到了左边界的位置,如果数组中压根没有 target 数据,那么当 L 和 R 指针相遇时的值就 != target ,所以我们要进行检验
为什么采用这种方法可以获得左边界的值呢?因为我们把数组划分为了两个区间【5,7,7】【8,8,10】,L 指针改变是移动到 mid+1 的位置,所以 L 指针会一直尝试跳出不符合添加的区间,而 R 指针一开始就在 <= target 的区间,R 指针发生移动也只是移动到 mid 的位置,所以 R 指针不会出 <= target 的区间,只会不断的靠近左边界的值,所以当 L 指针和 R 指针相遇时,便得到了左边界的位置
5 7 7 8 8 10
L
R
我们去寻找右边界也是一样的流程,将数组划分为【 5,7,7,8,8】【10】,【 5,7,7,8,8】<= target 的区间,【10】是大于 target 的区间
但是在查找左右边界时存在一个细节:在查找左区间时,中点 mid = left+(right-left)/2 ,而在查找右区间时,中点 mid = left+(right-left+1)/2,简单来说就是,当数据的个数为偶数时,中间节点有两个,如果查找的是左区间,就去左边的节点为中间节点,如果查找的是右区间就取右边的节点为中间节点,为什么呢?
因为不这样做会导致死循环,假设现在 输入:nums = [2,2], target = 2
现在我们要查找左区间,此时的中间节点有两个,我们用右边的节点做中间节点,此时 mid 指向的数据 2 是 >= target 区间的,所以不清楚 mid 此时指向的是否就是目标位置,所以让 R = mid,就相当于 R 没动,L 和 R 指针没有相遇,继续循环,就造成了死循环
2 2
L R
mid