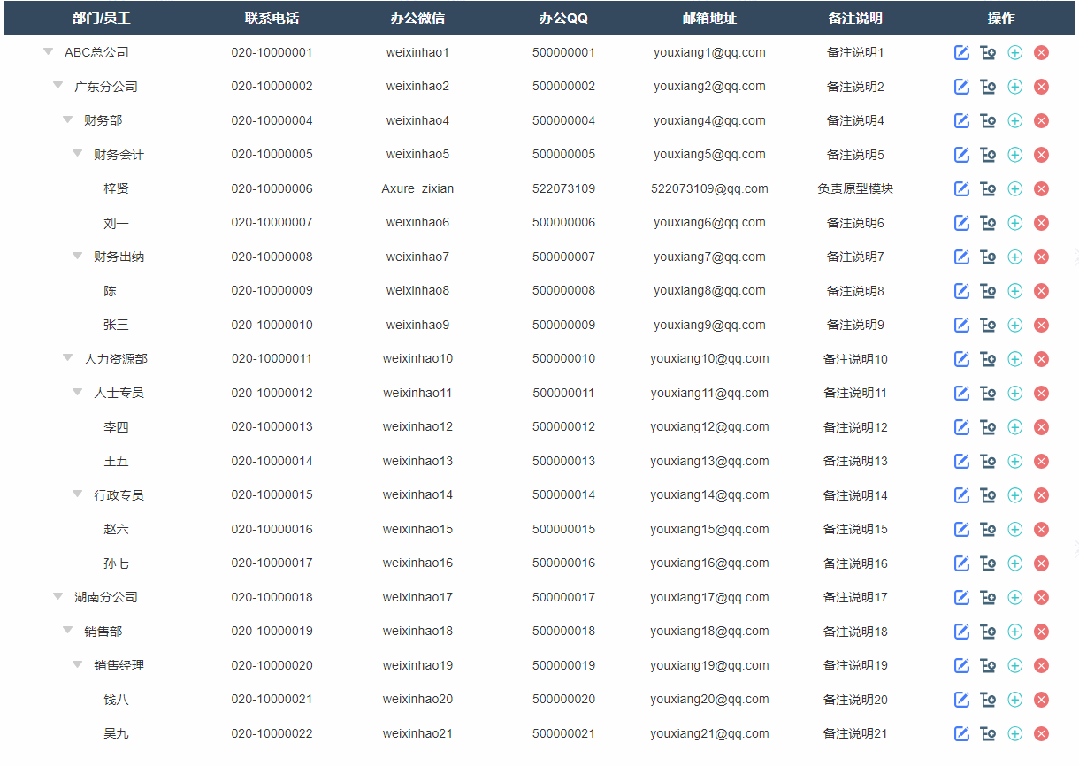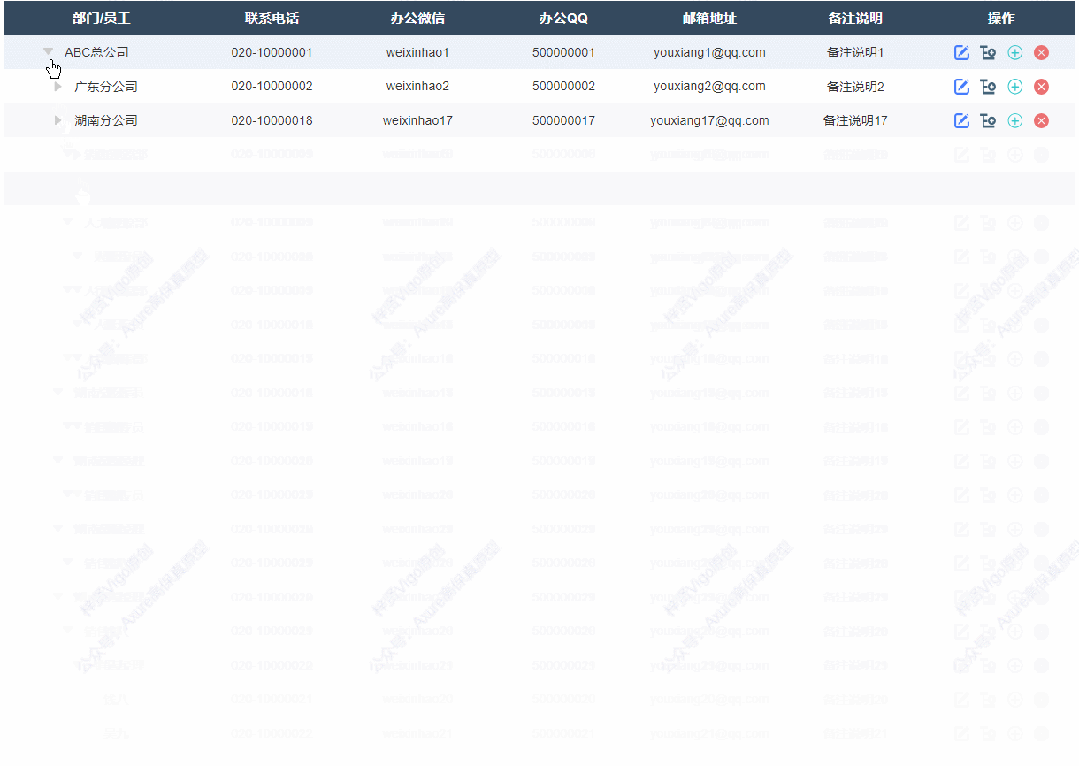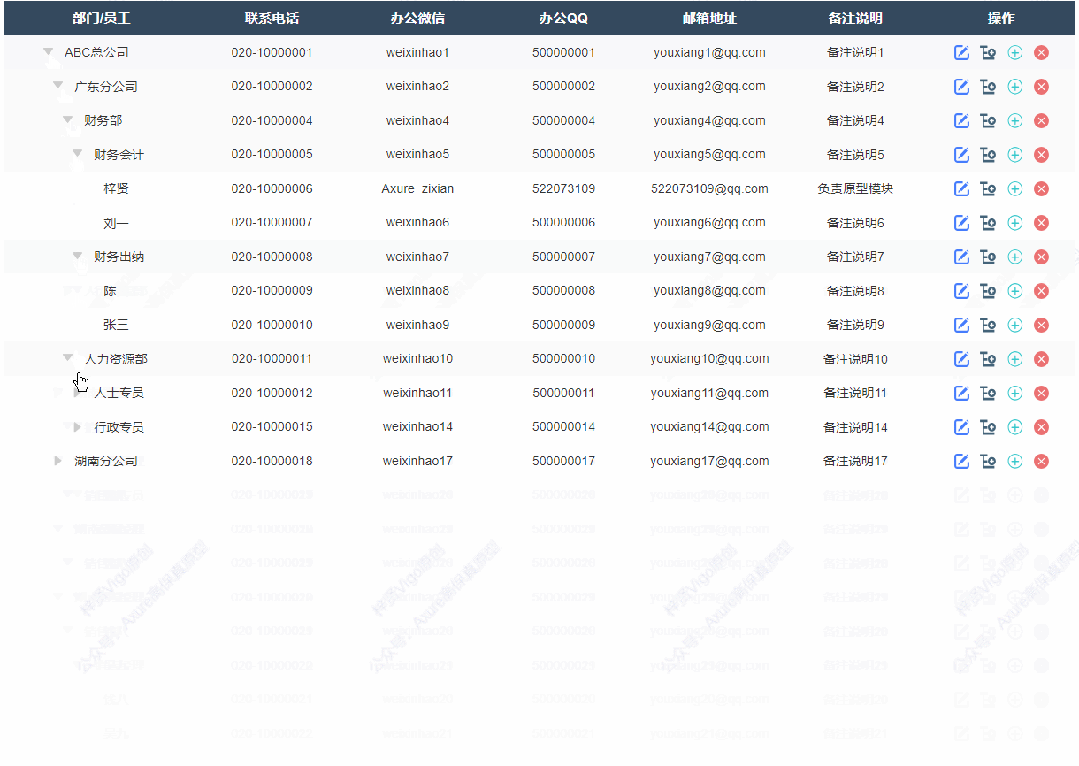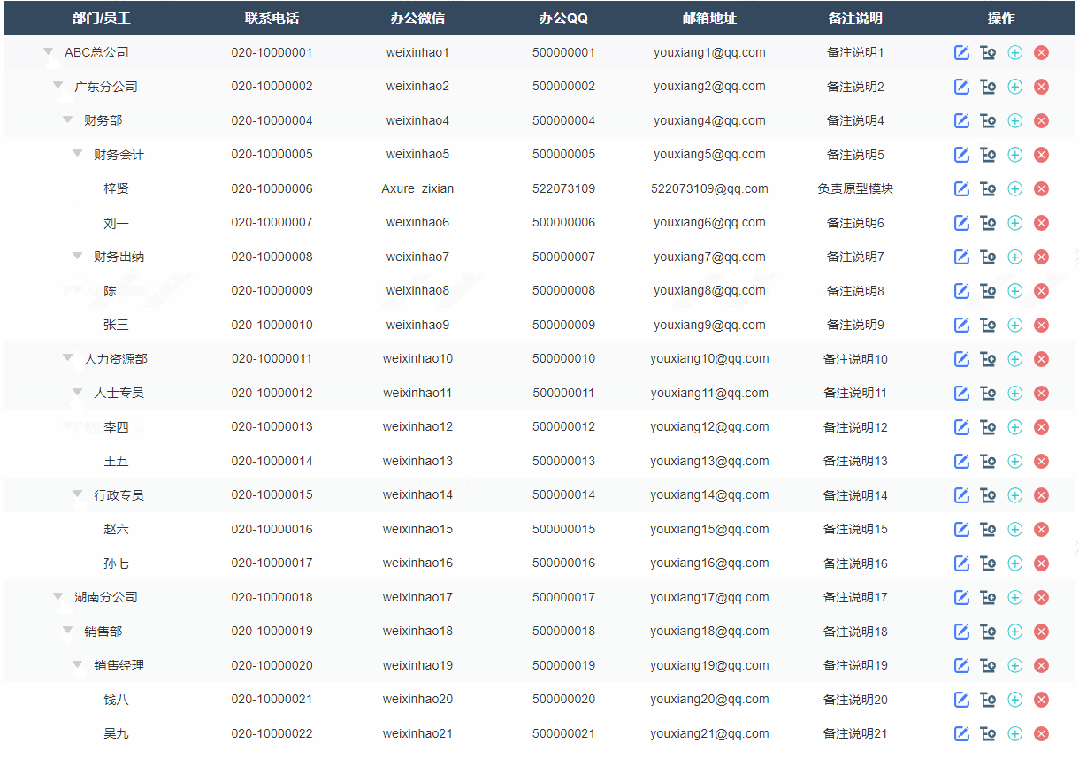
今天和大家分享能增删改的树形表格的原型模板，包括展开、折叠、增加、修改、删除表格内容，那这个原型模板是通过中继器制作的，所以使用简单，只需要填写中继器表格，即可自动生成对应的树形表格。这个模板最高支持6级树形表格，具体效果可以观看下方视频或者打开预览地址体验

【原型预览含下载地址】

https://axhub.im/ax9/ac73b98a296b6a85/#g=1&p=树形表格_增删改

【原型效果】

以下是部分效果

1、展开收起效果

点击可以切换展开或者收起子节点

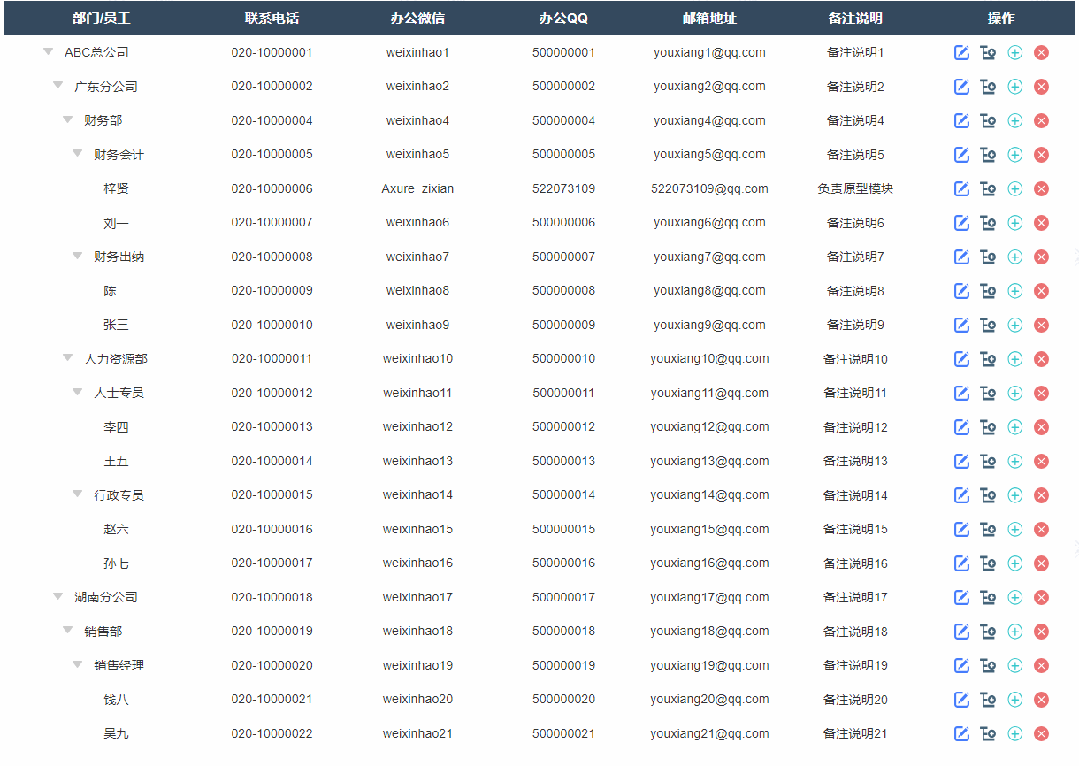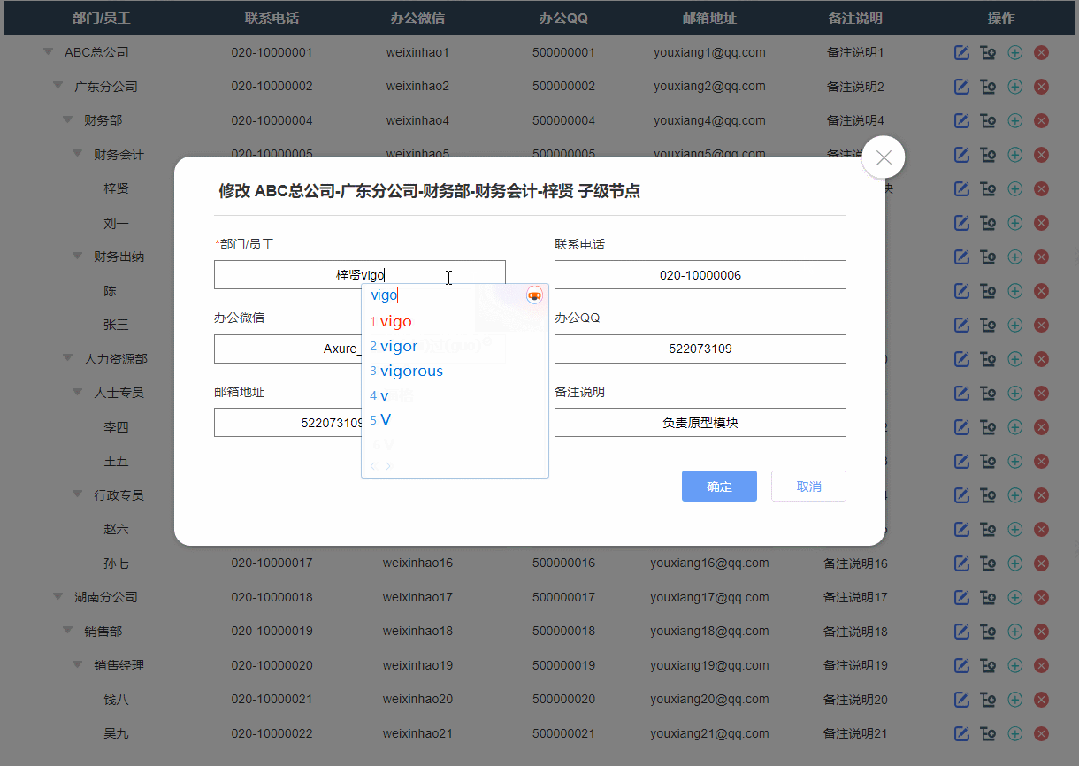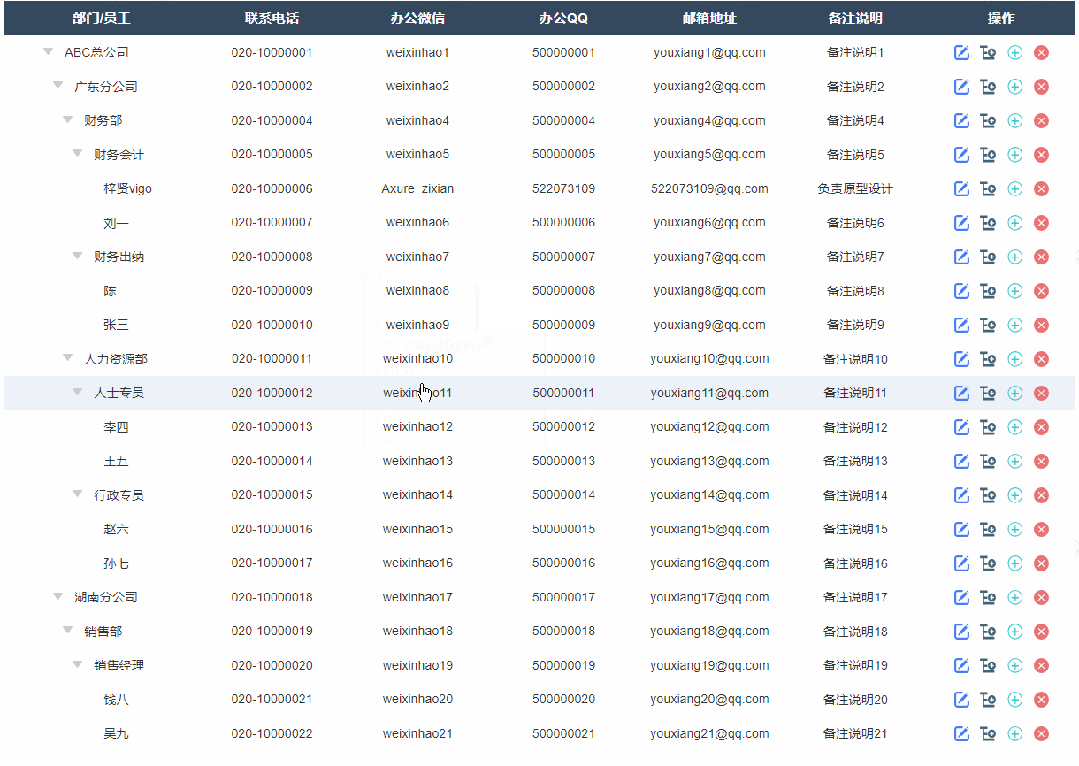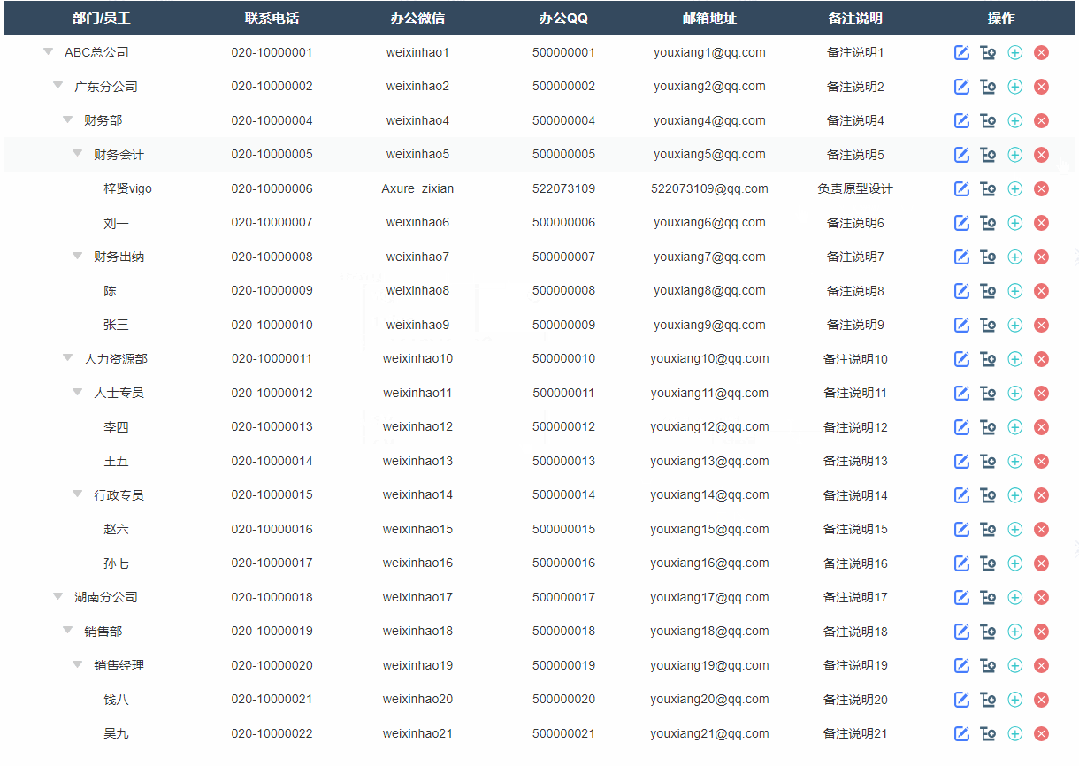
2、修改节点效果

点击修改按钮按钮后显示修改弹窗，修改完成确定后就可以在表格里看到修改后的数据

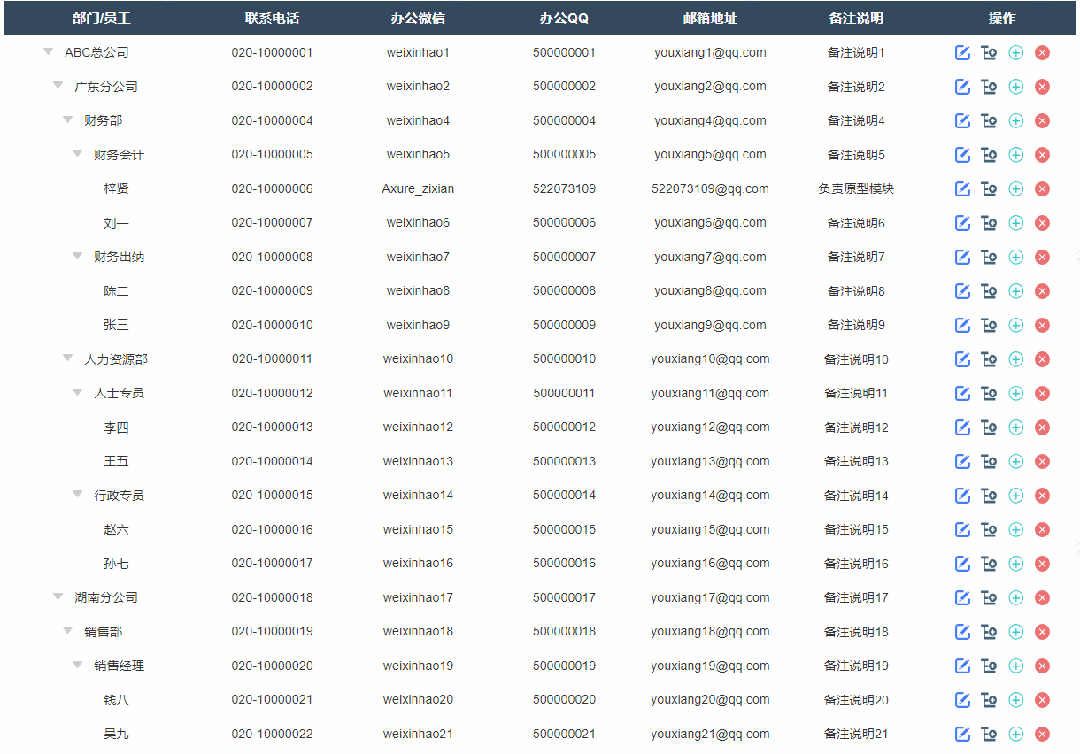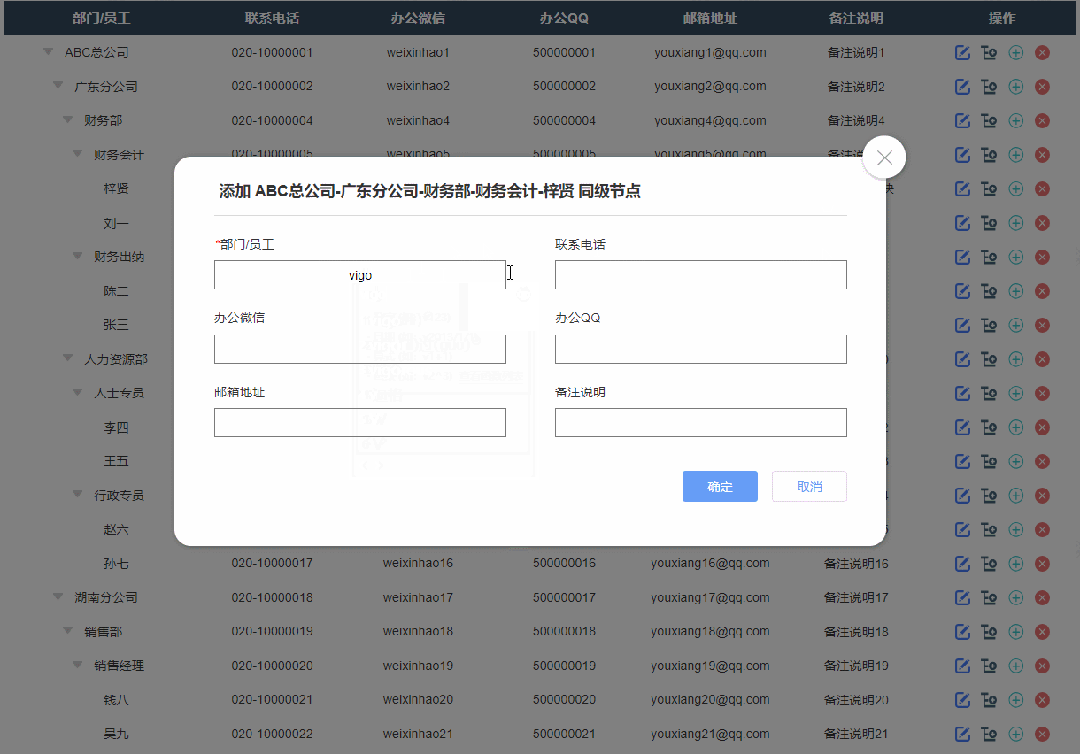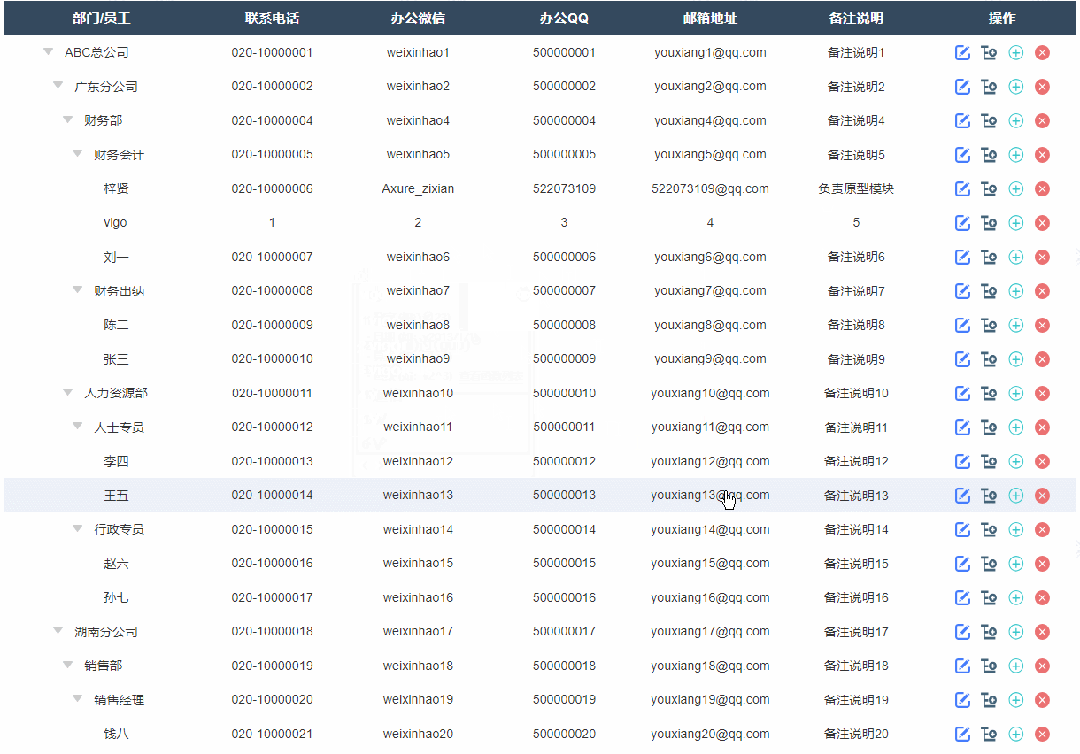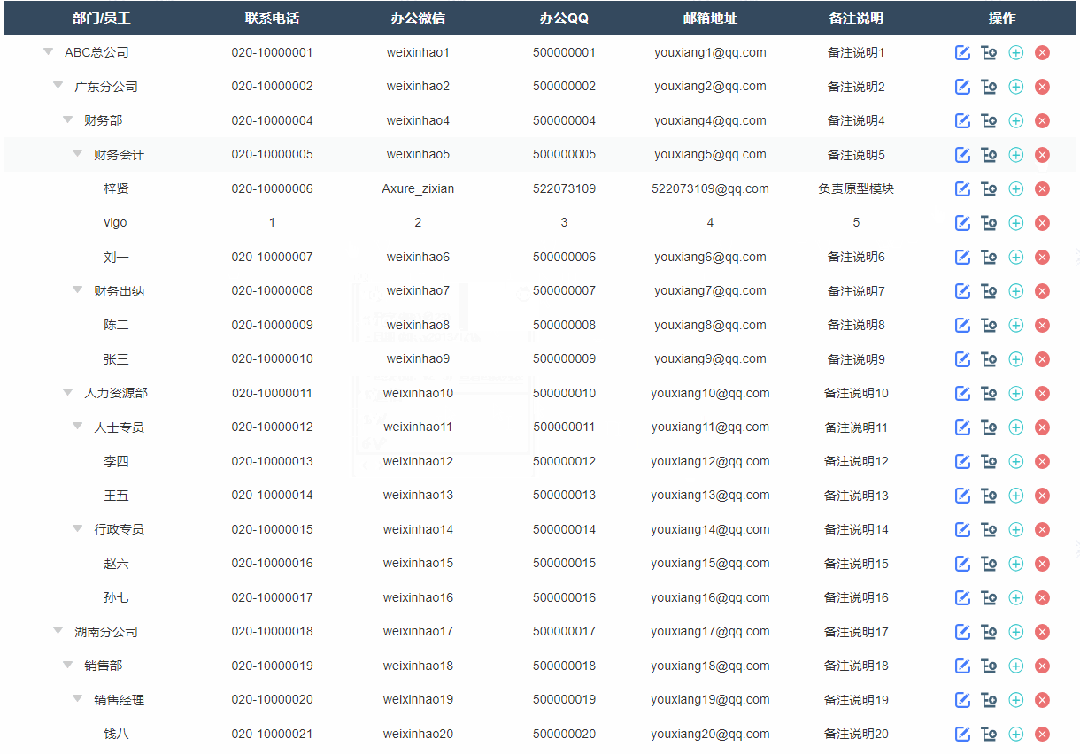
3、添加同级节点效果

点击添加同级节点按钮后显示添加弹窗，填写完成确定后就可以在表格里新增对应内容

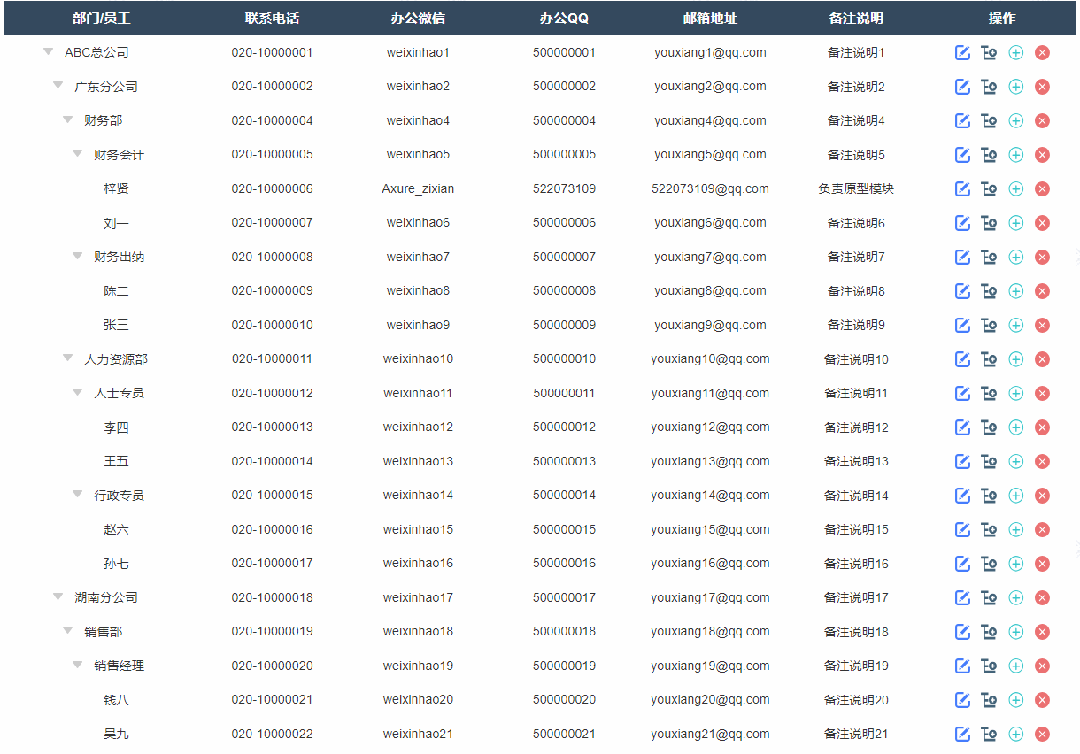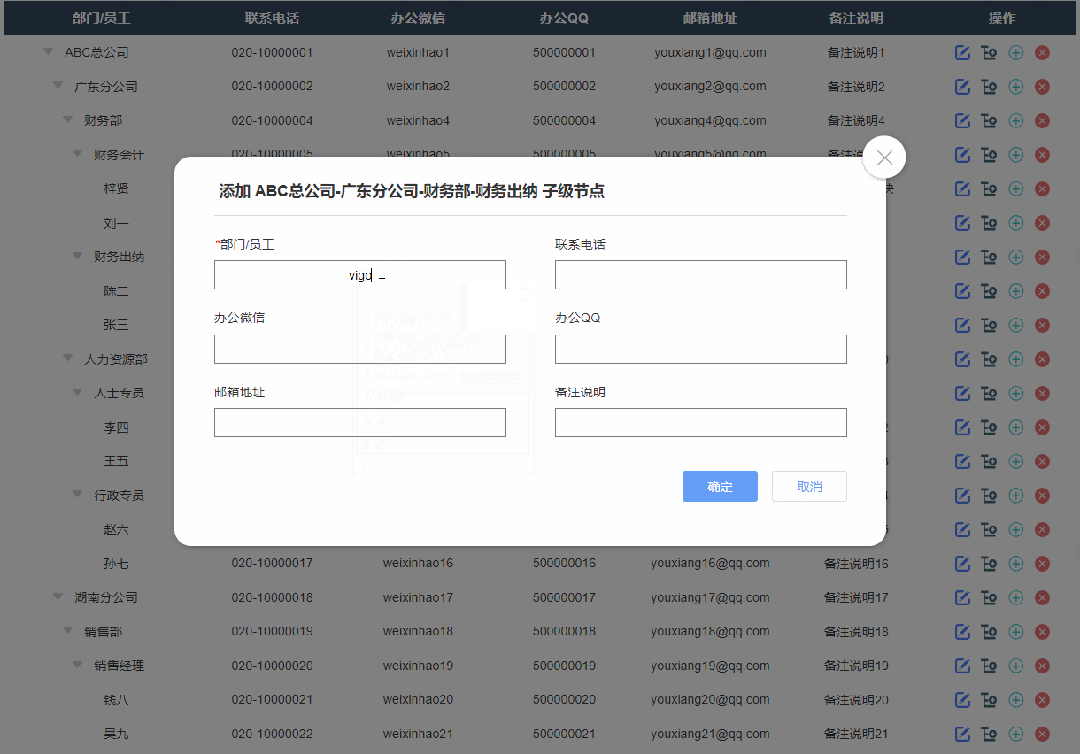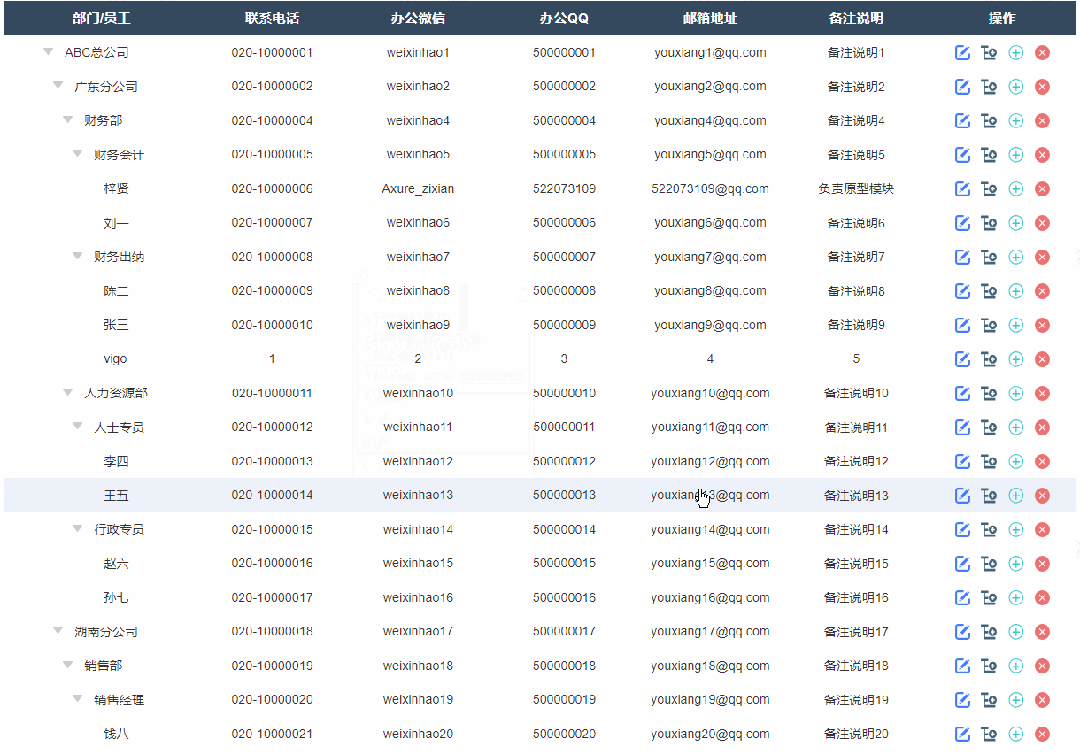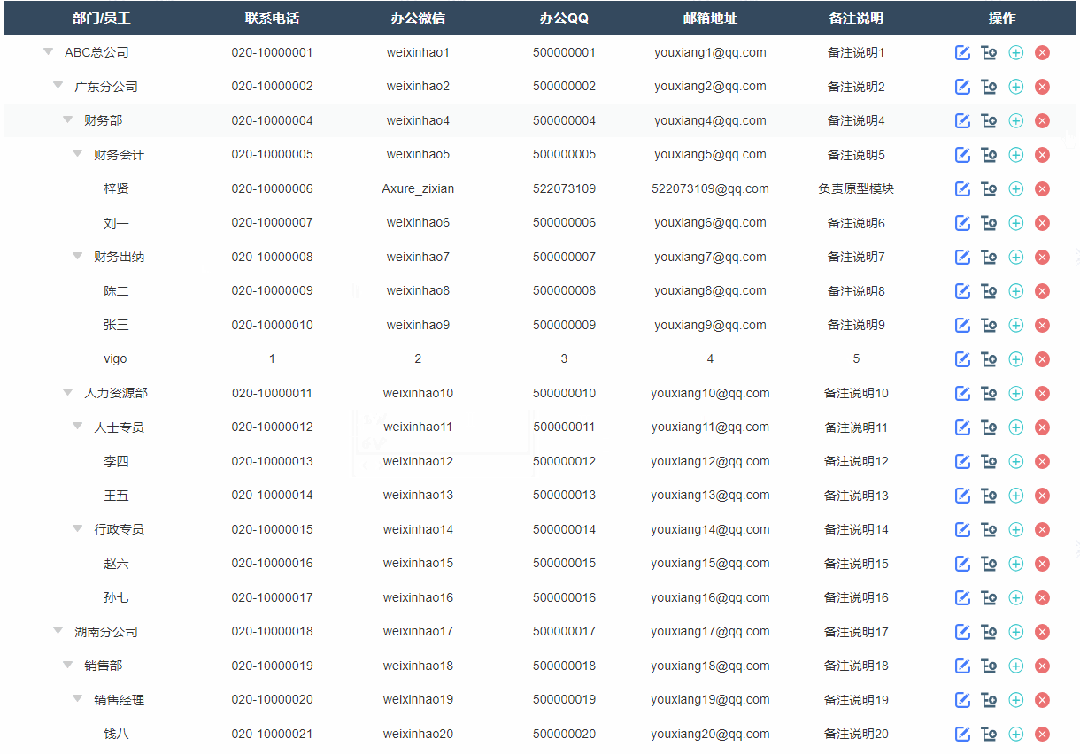
4、添加子级节点效果

点击添加子节点按钮后显示添加弹窗，填写完成确定后就可以在表格里新增对应子节点内容

5、删除节点效果

点击删除按钮，会弹出确认删除弹出，确认后删除选中节点及其子节点

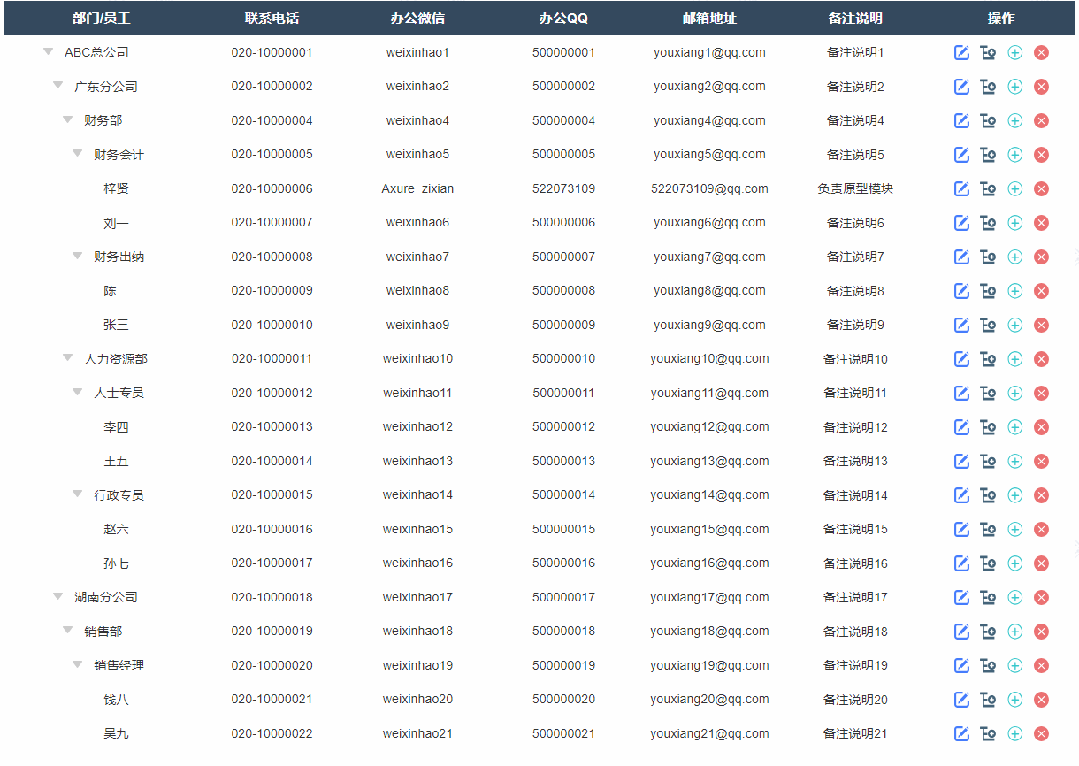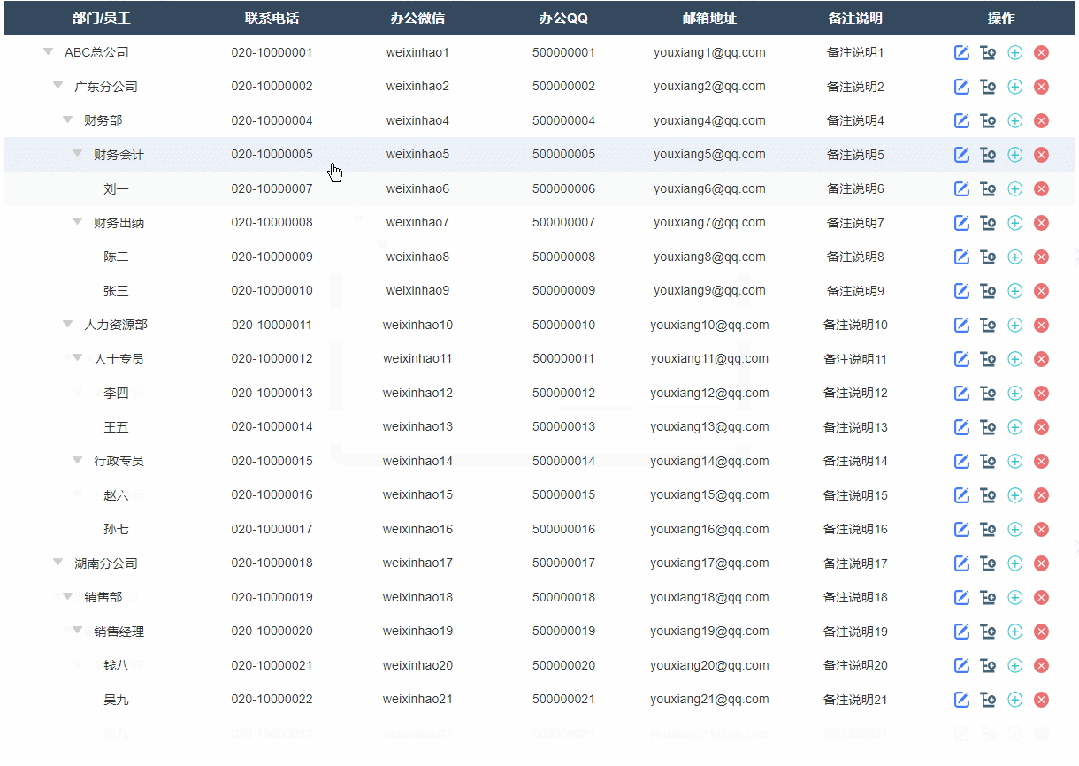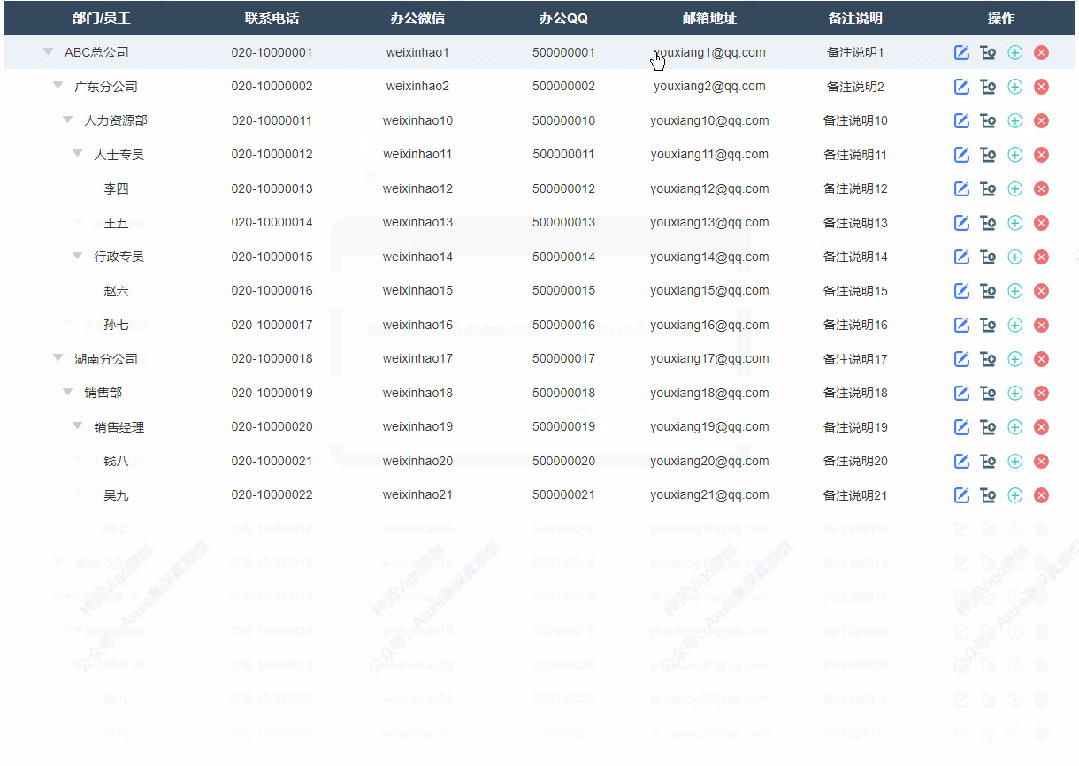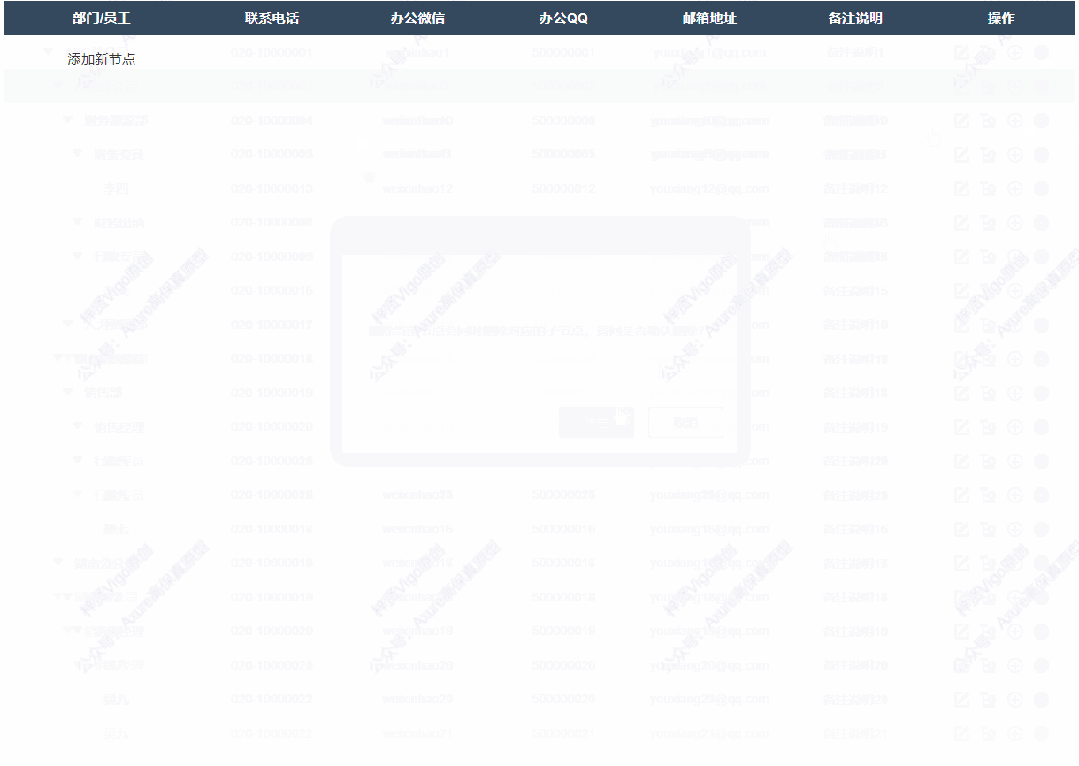
6、删除后新增按钮

如果删除了表格里所有数据，就会显示一个添加新节点的按钮，点击后显示添加弹窗，填写完成确定后就可以在表格里新增对应内容