- 密码体制的安全应当只取决于密钥的安全,而不取决于对密码算法的保密。
- 密钥管理包括密钥的产生、存储、分配、组织、使用、停用、更换、销毁等一系列技术问题
- 密钥管理问题分为:技术问题、管理问题、人员素质问题
- 密钥管理的原则:区分密钥管理的策略和机制、全程安全原则、最小权力原则、责任分离原则、密钥分级原则、密钥更换原则、密钥必须满足安全性指标、密码体制不同,密钥管理也不同
- 传统密码体制中密钥管理保护的是密钥的秘密性、真实性、完整性
- 密钥分级:初、中、高级密钥(一、二、三级密钥)
- 主密钥用真随机数,使用人工分配
- 密钥分配模式:利用公开密钥密码体制分配传统密码的密钥、Diffie-Hellma密钥分配方案
- Diffie-Hellman密钥分配协议 可中间人攻击

- 密钥的存储形态:明文形态、密文形态、分量形态(用于产生密钥的部分参数),主密钥只能明文存储
- 公钥密码体制需要保护公钥的完整性和真实性,私钥的秘密性、完整性、真实性
- 证书:经过签名的一组信息的集合
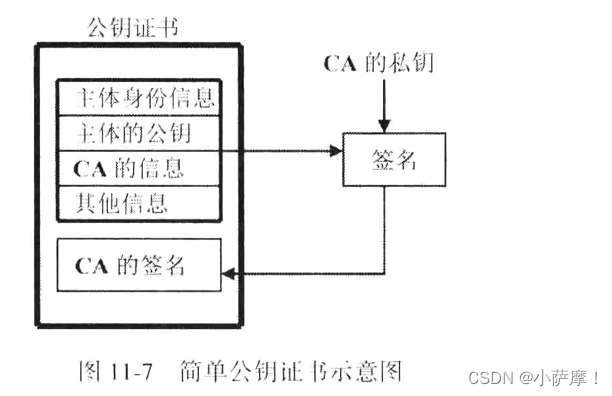
- PKI:公钥证书、证书管理机构、证书管理系统、围绕证书服务的各种硬件设备以及相应的法律基础共同组成公开密钥基础设施PKI
- 签证机构CA:签发证书、管理和撤销证书
- 注册机构:负责受理用户申请证书
【密码学引论】密钥管理
news2026/2/16 8:02:51
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1305749.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
掌握iText:轻松处理PDF文档-高级篇-添加水印
前言
iText作为一个功能强大、灵活且广泛应用的PDF处理工具,在实际项目中发挥着重要作用。通过这些文章,读者可以深入了解如何利用iText进行PDF的创建、编辑、加密和提取文本等操作,为日常开发工作提供了宝贵的参考和指导。
掌握iText&…
数字人er-nerf安装
目录
服务器环境
环境准备
1.下载源码
2.安装Ancoda环境
3.安装cudatoolkit
4.安装cuDNN
5.安装pytorch
6.安装requirements
7.安装tensorflow
8.安装pytorch3d
9.gcc安装
训练准备
训练 最近安装er-nerf,安装了很久,各种报错,我…
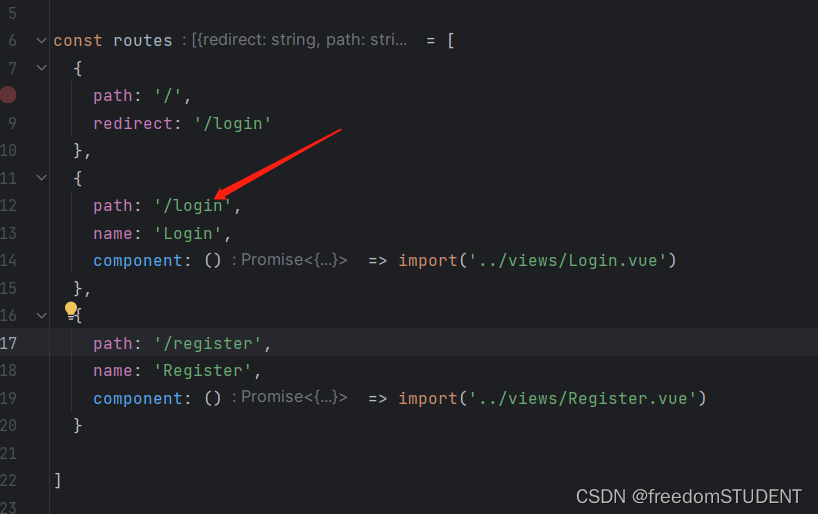
【Vue】router.push用法实现路由跳转
目录
router.push用法
在Login.vue中
在Register.vue中 上一篇:登录与注册界面的制作
https://blog.csdn.net/m0_67930426/article/details/134895214?spm1001.2014.3001.5502 制作了登录与注册界面,并介绍了相关表单元素即属性的用法 在登录页面…
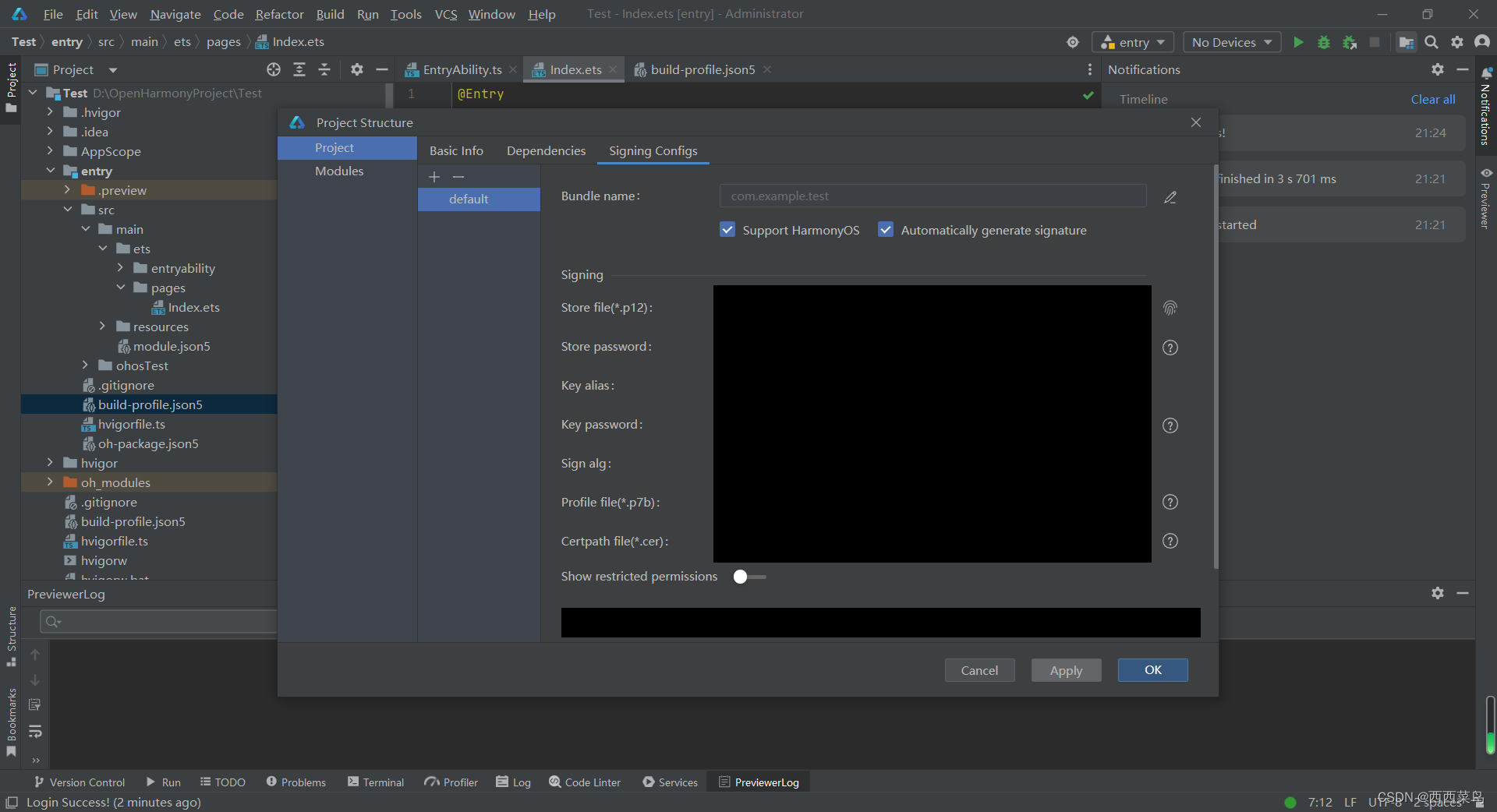
OpenHarmony应用开发——创建第一个OpenHarmonry工程
一、前言 本文主要介绍DevEco Studio的相关配置,以及创建第一个OpenHarmony应用程序。
二、详细步骤 打开DevEco Studio. 进入Settings. 随后SDK选择OpenHarmony,并完成下述API的选择与下载. 等待下载完成后,创建第一个Project. 此处选择Emp…
区块链技术的未来,了解去中心化应用的新视角
小编介绍:10年专注商业模式设计及软件开发,擅长企业生态商业模式,商业零售会员增长裂变模式策划、商业闭环模式设计及方案落地;扶持10余个电商平台做到营收过千万,数百个平台达到百万会员,欢迎咨询。
随着…
C/C++,动态 DP 问题的计算方法与源程序
1 文本格式
#include <bits/stdc.h>
using namespace std;
typedef long long LL;
const int maxn 500010; const int INF 0x3f3f3f3f;
int Begin[maxn], Next[maxn], To[maxn], e, n, m; int size[maxn], son[maxn], top[maxn], fa[maxn], dis[maxn], p[maxn], i…
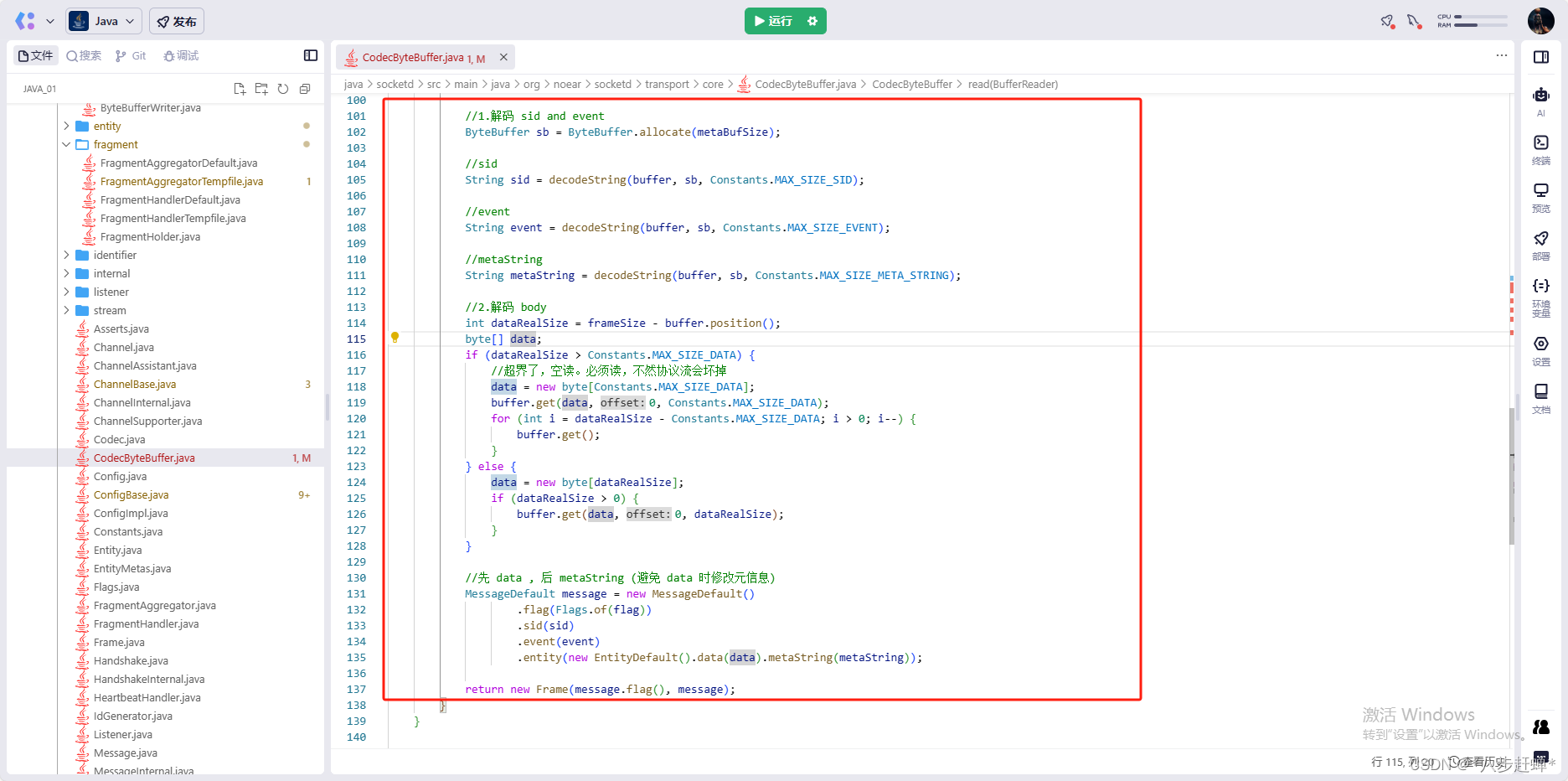
推荐开源项目-网络应用协议框架Socket.D
基于事件和语义消息流的网络应用协议 Socket.D 0 代码仓库地址1 该开源项目特点2 项目结构3 核心理念-协议帧Frame4 结束语 0 代码仓库地址
https://gitee.com/noear/socketd
1 该开源项目特点
代码风格优雅文档说明齐全测试用例非常人性化上手快,代码用例很多代…
基于双树复小波变换和稀疏表示的多光谱和彩色图像融合算法matlab仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1 双树复小波变换原理
4.2 稀疏表示原理
4.3 基于双树复小波变换和稀疏表示的图像融合算法
5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本
MATLAB2022a
3.部分核心程序…
Appium 自动化自学篇 —— 初识Appium自动化!
Appium 简介
随着移动终端的普及,手机应用越来越多,也越来越重要。而作为测试 的我们也要与时俱进,努力学习手机 App 的相关测试,文章将介绍手机自动化测试框架 Appium 。 那究竟什么是 Appium 呢? 接下来我们一起来学习PythonS…
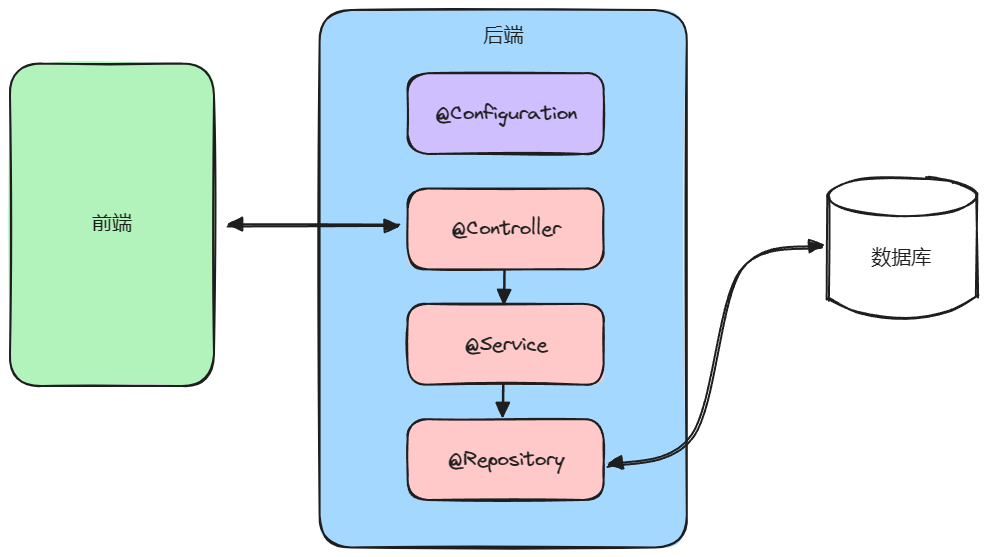
Spring 的设计思想、创建和使用、Bean 作用域和生命周期
文章目录 Spring 设计思想Spring 是什么?什么是 IoC? Spring 创建和使用创建 Spring 项目注册 Bean 对象获取并使用 Bean 对象 Spring 更方便地存储和读取对象配置文件使用注解使用类注解使用方法注解 获取 Bean 对象属性注入Setter 注入构造方法注入Res…
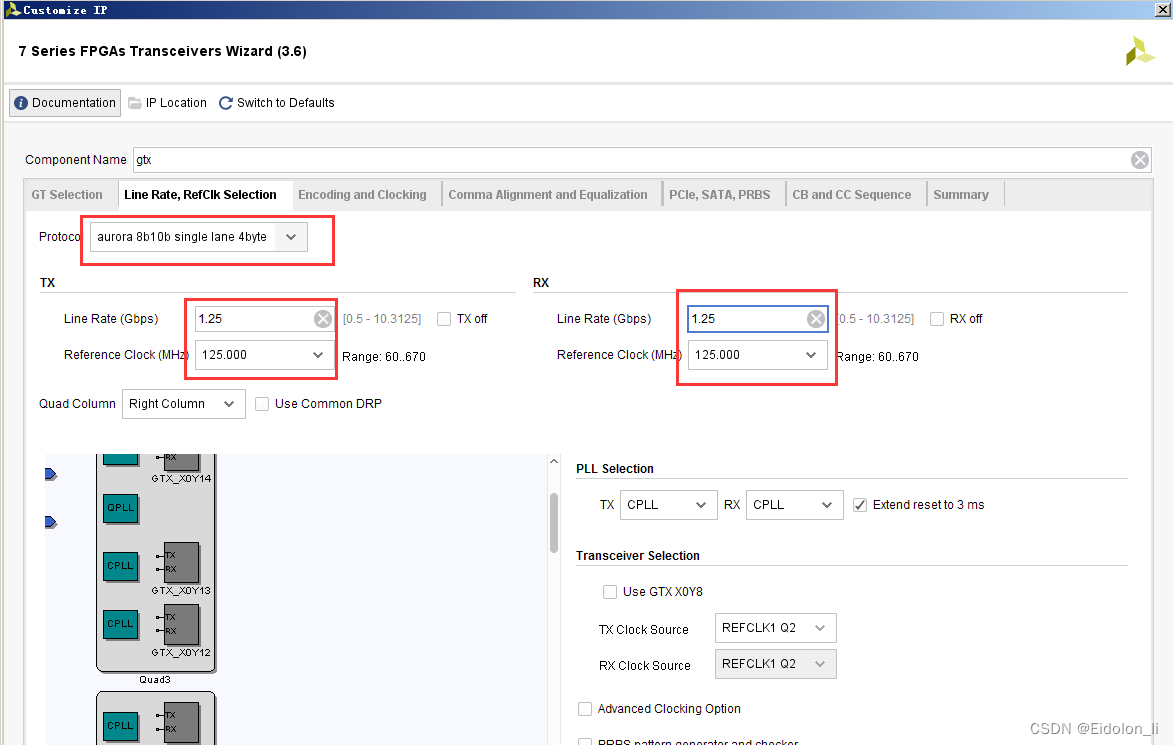
基于FPGA的视频接口之高速IO(光纤)
简介 对于高速IO口配置光纤,现在目前大部分开发板都有配置,且也有说明,在此根据自己的工作经验以及对于各开发板的说明归纳 通过高速IO接口,以及硬件配置,可以实现对于光纤的收发功能,由于GTX的速率在500Mbs到10Gbps之间,但通道高速io可配置光纤10G硬件,物理通完成,则…
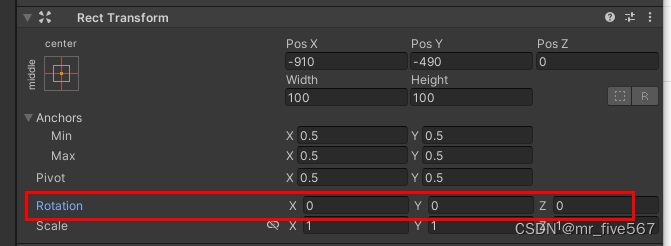
Unity 修改游戏对象的旋转角度Rotation的方法
在Unity中要修改游戏对象中的旋转角度,即下图中的Rotation: 有三个方法:
1、 使用欧拉角(Euler Angles):欧拉角是一组表示旋转的三个角度值(绕X轴的旋转、绕Y轴的旋转和绕Z轴的旋转)。
transf…
Unity光照模型实践
光照作为3D渲染中最重要的部分之一,如何去模拟真实环境的光照是重要的研究内容,但是现实环境光照过于复杂,有很多经典好用的光照模型去近似真实光照。
根据基础的Phong模型 最终某个点的结果为 环境光Ambient 漫反射光Diffuse 高光Specula…
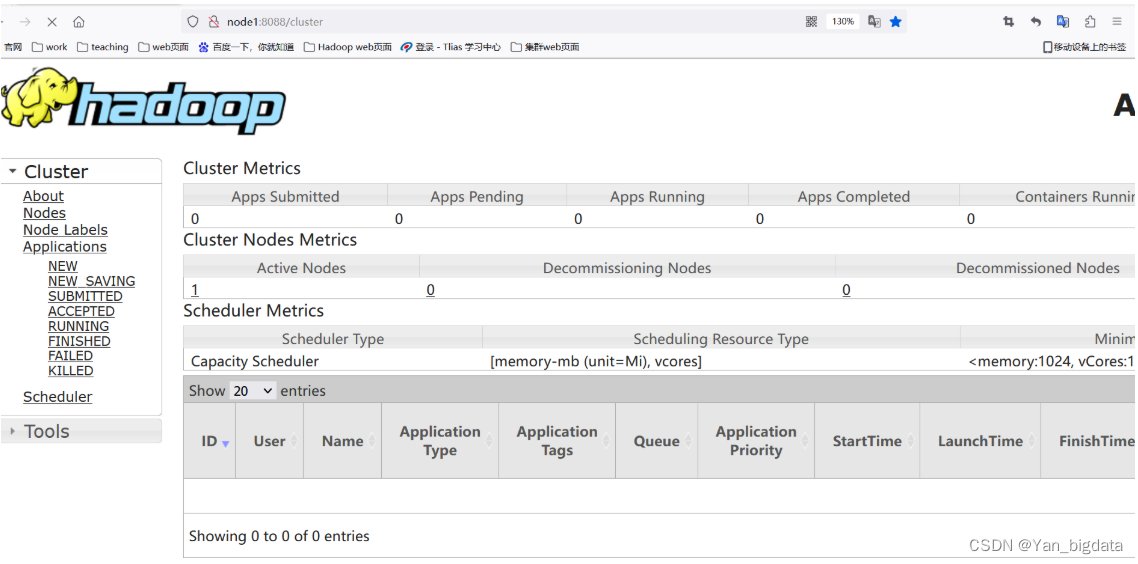
Hadoop高可用(主备切换)---配合Zookeeper
1. Hadoop高可用(Hadoop High Availability)概述
HA(High Available), 高可用,是保证业务连续性的有效解决方案,一般有两个或两个以上的节点,分为活动节点(Active)及备用节点(Standby)。通常把…
Mendix 创客访谈录|合作伙伴谈Mendix对销售团队的业务价值
本期创客 段晓科 适途科技 咨询中心负责人 大家好,我叫段晓科,非软件开发专业,拥有多年制造行业数字化解决方案经验,擅长从0到1 的产品构建和产品落地服务。
目前任职于适途科技,自2021年3月至今负责Mendix低代码平台…
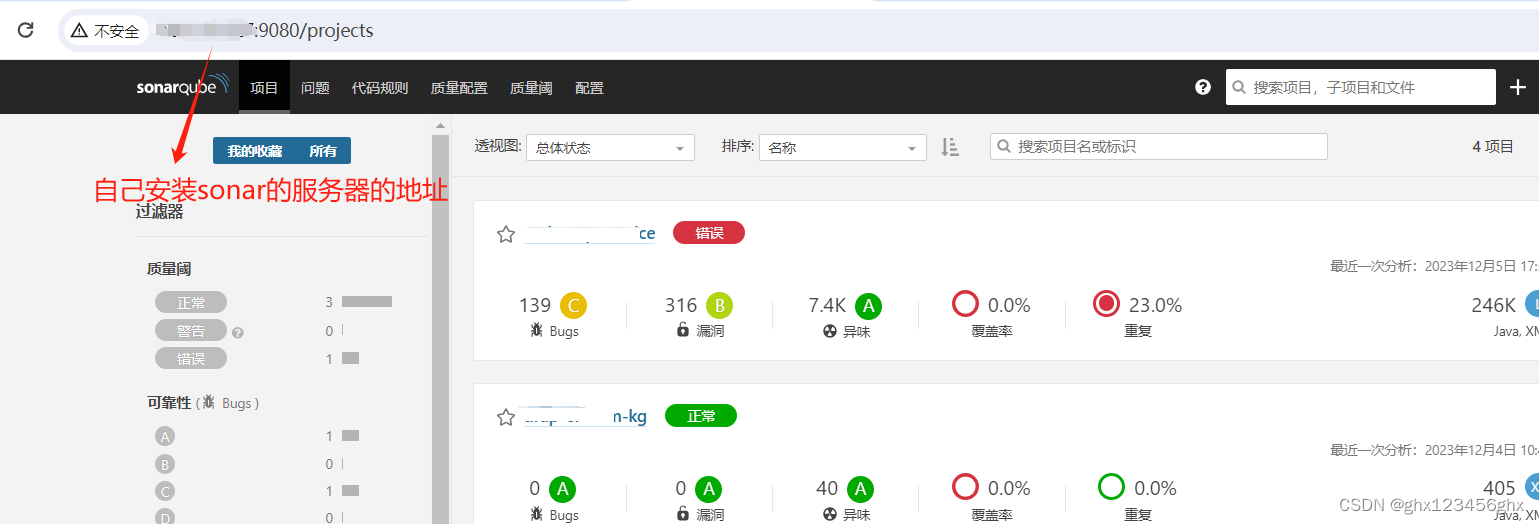
sonar扫描代码用法
1 mvn的setting配置文件中配置如下
其中sonar.host.url是本地或者服务器上自己安装的sonar <pluginGroups><pluginGroup>org.sonarsource.scanner.maven</pluginGroup></pluginGroups><profile><id>sonar</id><activation>&l…
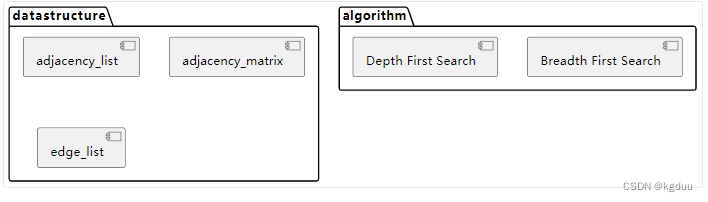
boost graph之基础
结构 属性相关 #mermaid-svg-PZQvKfbwNSnyXO9g {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-PZQvKfbwNSnyXO9g .error-icon{fill:#552222;}#mermaid-svg-PZQvKfbwNSnyXO9g .error-text{fill:#552222;stroke:#5522…
文心一言 VS 讯飞星火 VS chatgpt (155)-- 算法导论12.3 2题
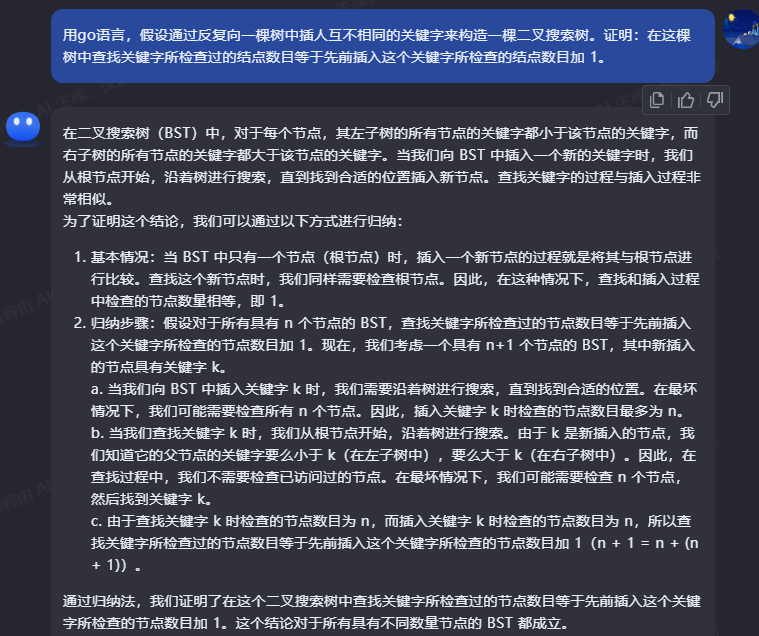
二、用go语言,假设通过反复向一棵树中插人互不相同的关键字来构造一棵二叉搜索树。证明:在这棵树中查找关键字所检查过的结点数目等于先前插入这个关键字所检查的结点数目加 1。
文心一言:
为了证明这个结论,我们可以使用二叉搜…
【代码随想录】刷题笔记Day34
前言
考过概率论,发过一场烧,兜兜转转又一月,轻舟已撞万重山,赶紧刷题
贪心算法理论基础
贪心的本质:局部最优→全局最优无套路,常识性推导 举反例
455. 分发饼干 - 力扣(LeetCode…