此动态规划系列主要讲解大约10个系列【后续持续更新】
本篇讲解入门级:斐波那契模型,会在讲解题目同时给出AC代码
为什么叫斐波那契数列模型?因为本篇4道题的状态转移方程都跟斐波那契递推方程差不多,但这点不重要,请往下看
目录
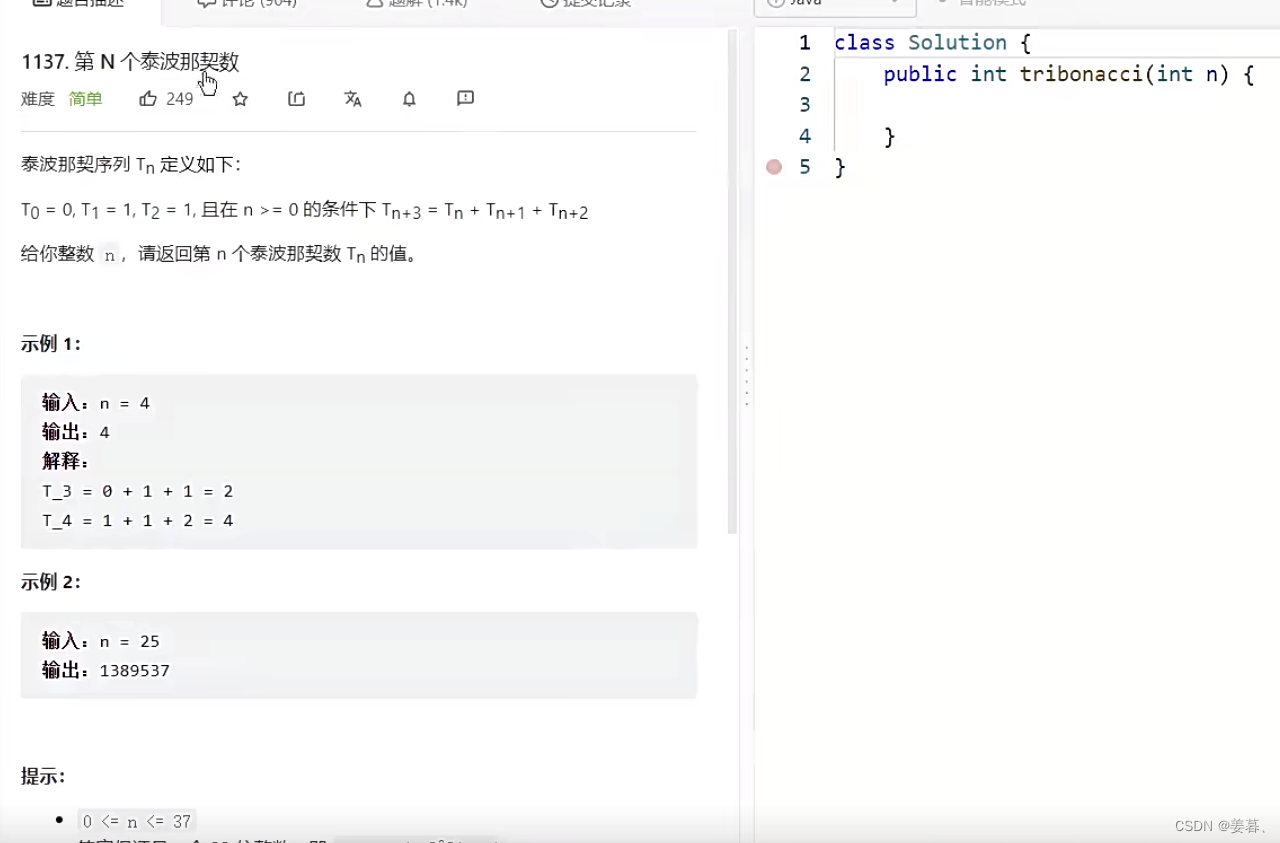
1、泰波那契数
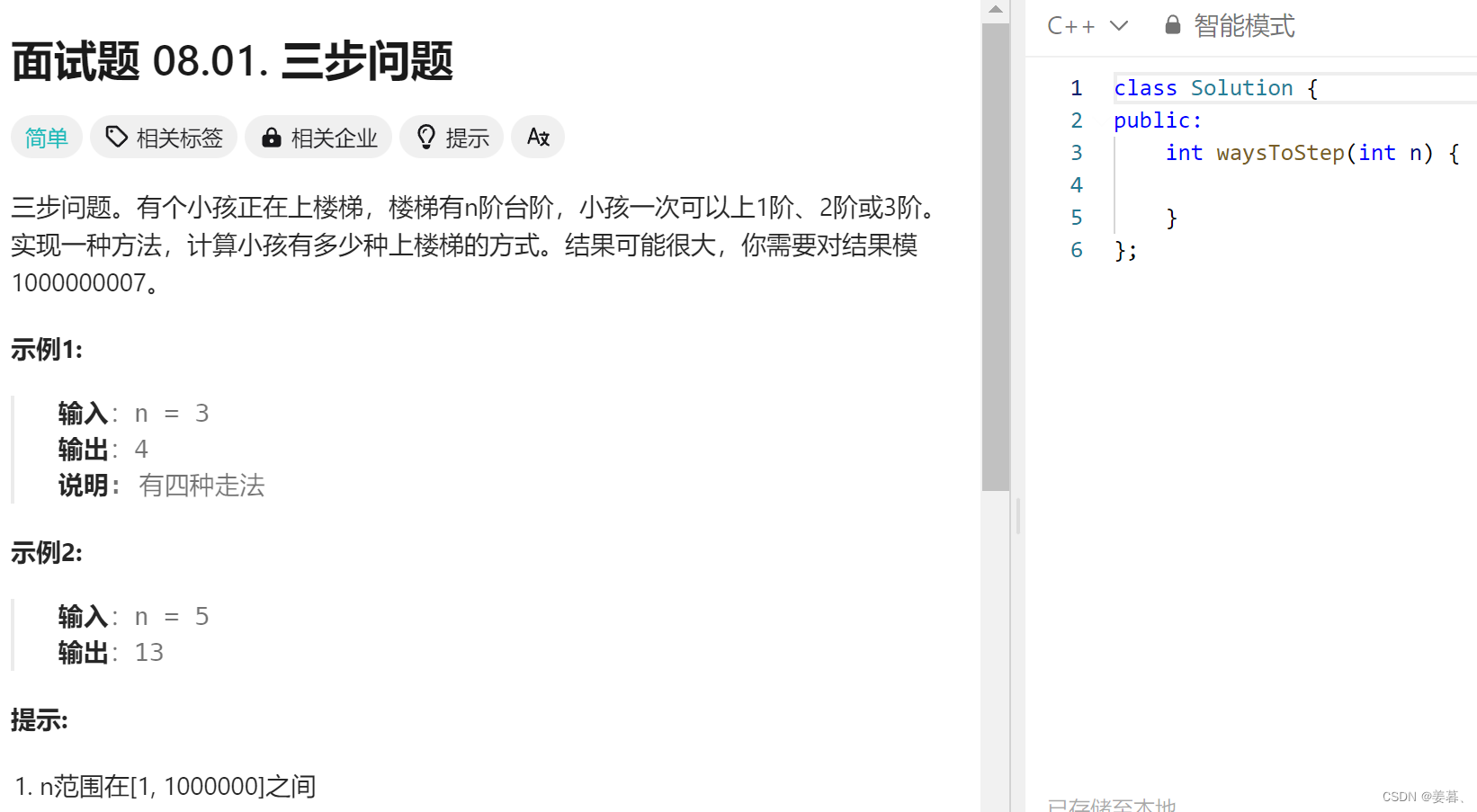
2、三步问题
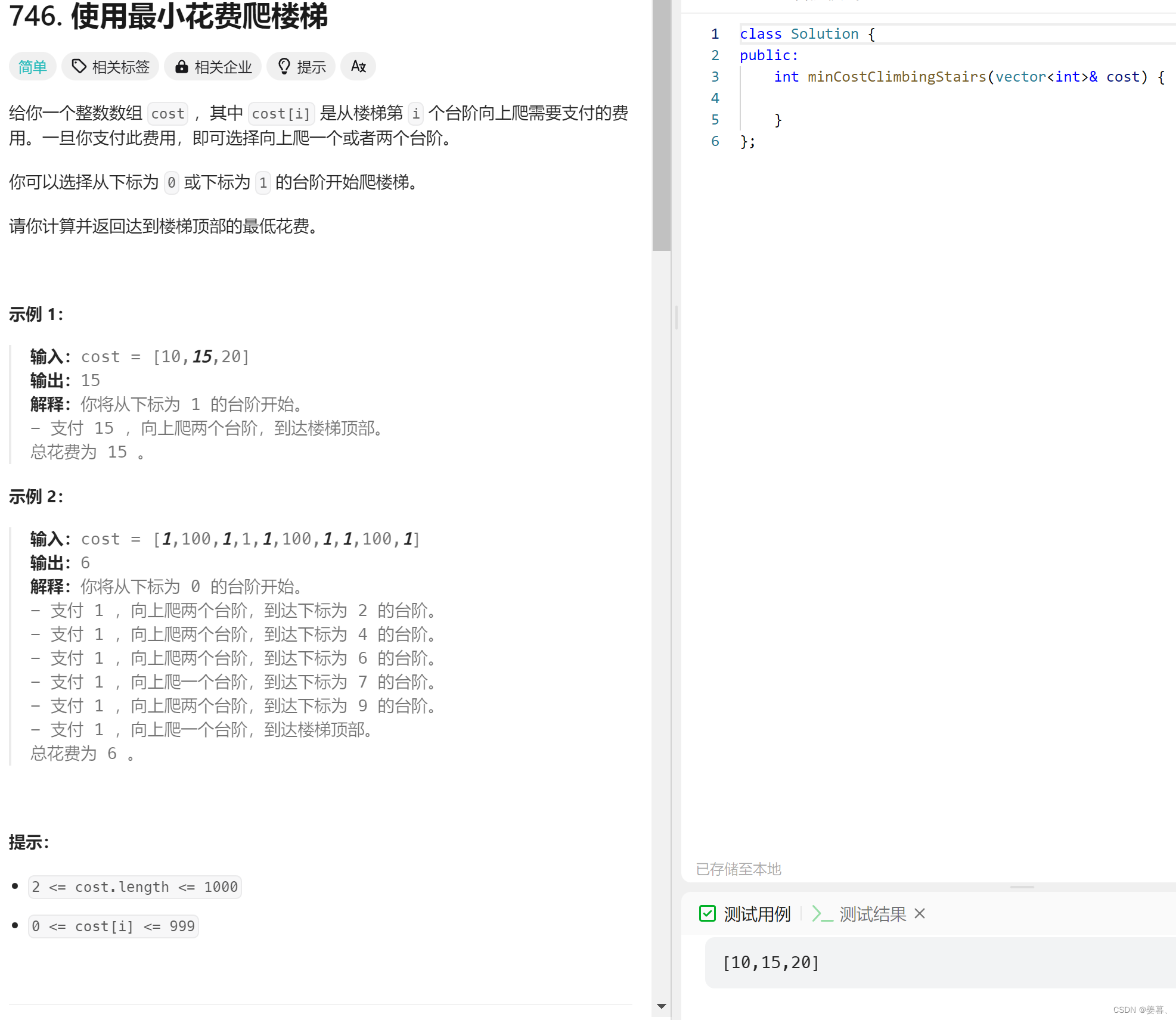
3、使用最小花费爬楼梯
4、解码方法
1、泰波那契数
我们动态规划首先是填dp表,填满dp表后,里面的某个值就是我们要求的最终结果(本题很简单,状态转移方程都直接给你了)
class Solution {
public:
int tribonacci(int n) {
//1、创建dp数组
//2、初始化
//3、填表
//4、返回值
//处理一下边界情况,若不处理下面到转移方程那里会越界
if (n == 0) return 0;
if (n == 1 || n == 2) return 1;
vector<int> dp(n + 1);//多开一个,因为我们会算到第n个数
dp[0] = 0, dp[1] = dp[2] = 1;
for (int i = 3; i <= n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
return dp[n];//返回第n个泰波那契数
}
};空间优化:
因为我们上述代码中空间复杂度是O(N),利用滚动数组思想可以实现O(1)
注:这种滚动数组我们以后笔试不要求,但是面试时可能有点研究价值,所以对于这个东西不用过分研究,但是注意后面讲解背包问题时会使用这个思想
class Solution {
public:
int tribonacci(int n) {
//处理一下边界情况,防止下面填表直接越界了
if (n == 0) return 0;
if (n == 1 || n == 2) return 1;
int a = 0, b = 1, c = 1, d = 0;
for (int i = 3; i <= n; i++)
{
d = a + b + c;
//滚动操作
a = b;
b = c;
c = d;
}
return d;
}
};2、三步问题
class Solution {
public:
int waysToStep(int n) {
//1、创建dp数组
//2、初始化
//3、填表
//4、返回值
const int MOD = 1e9 + 7;
//处理边界条件
if (n == 1 || n == 2) return n;
if (n == 3) return 4;
vector<int> dp(n + 1);
dp[1] = 1, dp[2] = 2, dp[3] = 4;
for (int i = 4; i <= n; i++)
{
//结果取模,必须对每一次加法的结果都取一次模,不能全加完再取模
dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;
}
return dp[n];
}
};3、使用最小花费爬楼梯
解法一:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
//1、创建dp表
//2、初始化
//3、填表
//4、返回值
int n = cost.size();
vector<int> dp(n + 1);//你不传初始值的话vector默认把值初始化为0
for (int i = 2; i <= n ; i++)
{
//到第i个台阶的花费=min(到第i-2个台阶的最小花费后再跨两步的花费,
//到第i-1个台阶的最小花费后再跨一步的花费)
dp[i] = min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
}
return dp[n];
}
};解法二:
注:解法二不用多开一个位置,因为是把最后两个位置初始化后往前推,从而得出最终结果
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n);
//从n-2到终点一定是一下跨两步,故cost[n - 2]即可
dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2];
for (int i = n - 3; i >= 0; i--)
{
dp[i] = cost[i] + min(dp[i + 1], dp[i + 2]);
}
return min(dp[0], dp[1]);
}
};总结:
状态表示有很多种,但是状态表示是否对要看你能够写出状态转移方程求解出问题,动态规划的题目需要大量经验,经验足够后再写状态表示等就会很熟练了
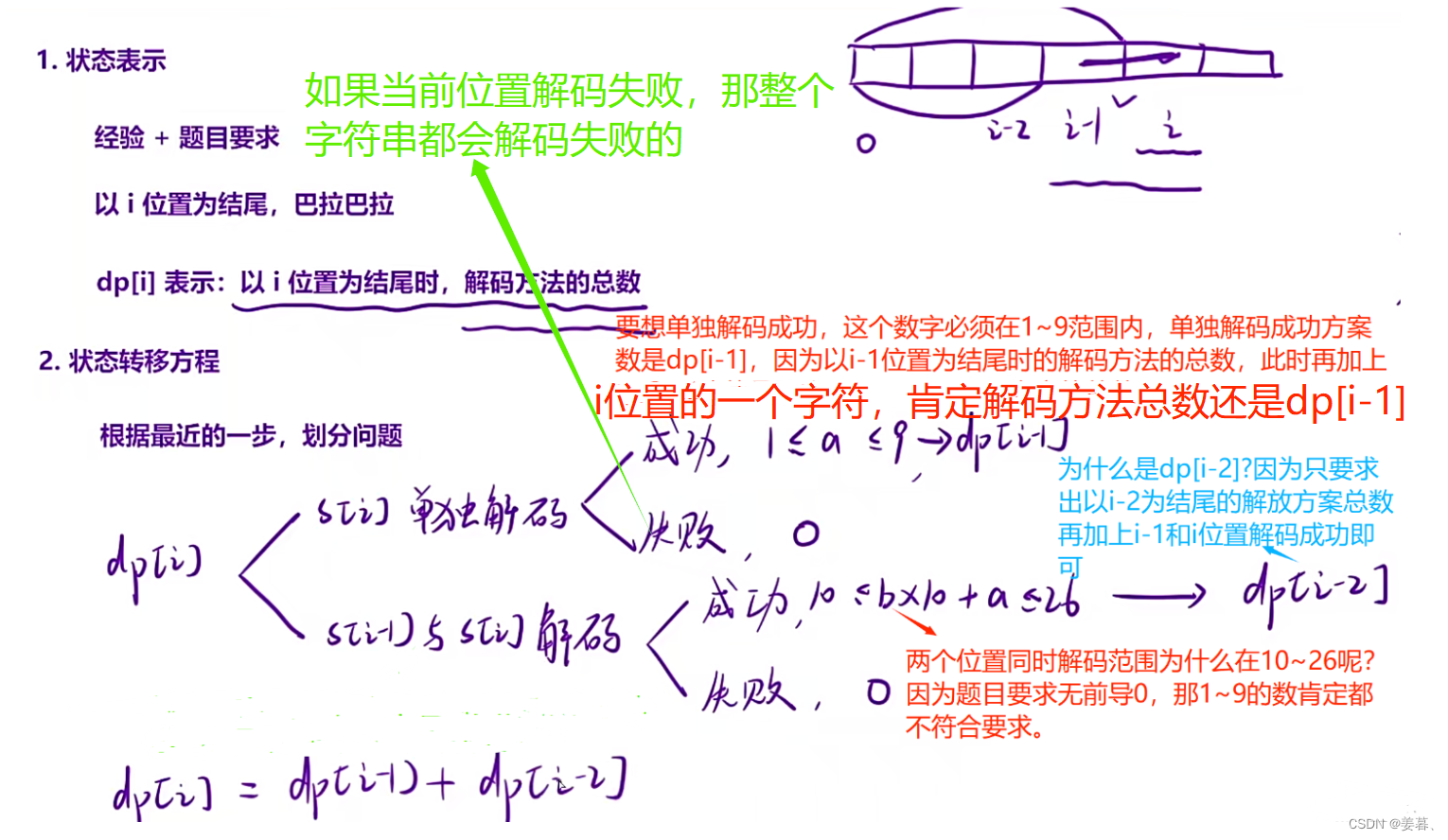
4、解码方法
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n);
//初始化dp[0]
dp[0] = s[0] != '0';//只要第一个字符不是'0',就可以单独编码
if (n == 1) return dp[0];
//初始化dp[1]
if(s[0] != '0' && s[1] != '0') dp[1] += 1;//两数字可以单独编码的情况
int con = (s[0] - '0') * 10 + s[1] - '0';
//共同编码的结果在10~26就是成功的,因为0~9会有前导0,就失败了
if (con >= 10 && con <= 26) dp[1] += 1;
for (int i = 2; i < n; i++)
{
//计算以i位置结尾的解码方案数
if (s[i] != '0') dp[i] += dp[i - 1];
int con = (s[i - 1] - '0') * 10 + s[i] - '0';
if (con >= 10 && con <= 26) dp[i] += dp[i - 2];
}
return dp[n - 1];
}
};优化:
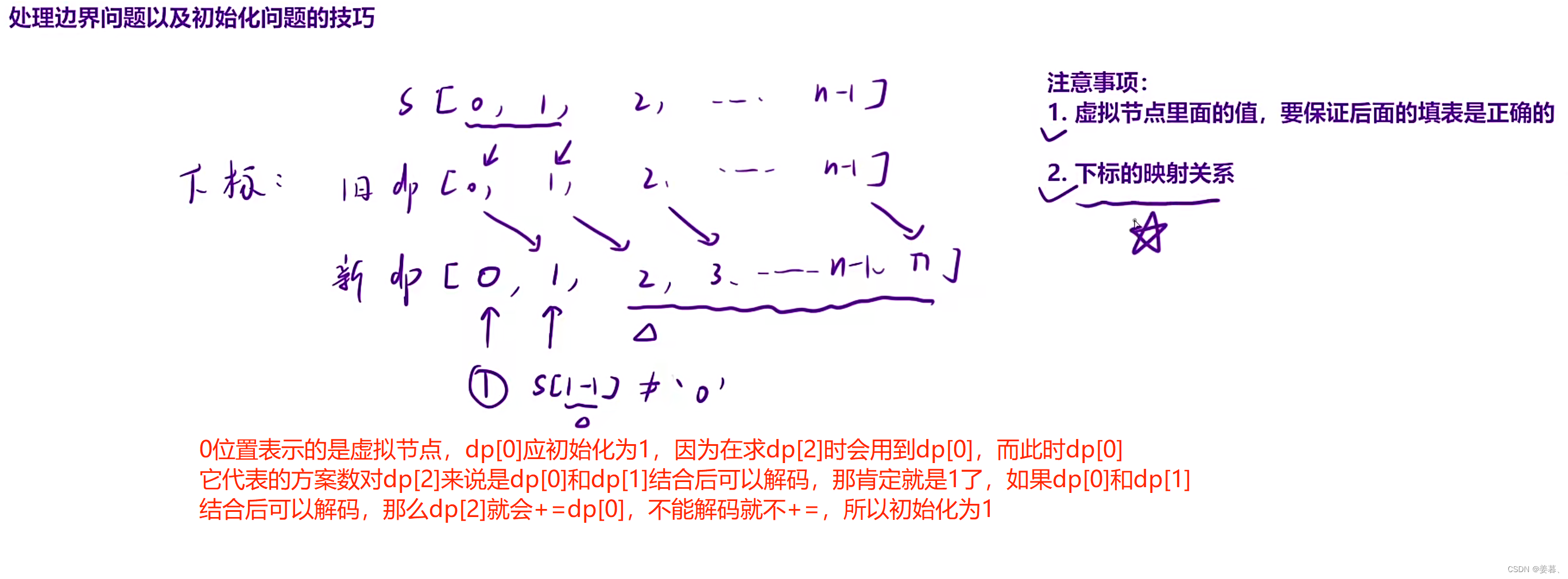
因为在计算以1位置结尾时的解放方案数与在计算从2位置往后的代码类似,所以我们可以做一个优化,让以1位置结尾的计算也在for循环中进行
class Solution {
public:
int numDecodings(string s) {
//优化
int n = s.size();
vector<int> dp(n + 1);
dp[0] = 1;//保证后续填表正确
dp[1] = s[1 - 1] != '0';
for (int i = 2; i <= n; i++)
{
//计算以i位置结尾的解码方案数
if (s[i - 1] != '0') dp[i] += dp[i - 1];
int con = (s[i - 2] - '0') * 10 + s[i - 1] - '0';
if (con >= 10 && con <= 26) dp[i] += dp[i - 2];
}
return dp[n];
}
};