一.思想

归并排序是一种基于分治思想的经典排序算法。其主要思想可以总结为以下几个步骤：

1. 分解（Divide）： 将原始序列划分为若干子序列，直到每个子序列包含一个或零个元素，即认为这些子序列是有序的。

2. 解决（Conquer）： 对每个子序列进行递归排序。如果子序列的长度为1或零，那么它被认为是有序的。否则，对子序列递归应用归并排序。

3. 合并（Merge）： 将已排序的子序列合并为一个新的有序序列。这是通过比较每个子序列的头部元素，选择最小的元素放入新序列，然后将相应子序列的指针向后移动一步，直到所有的子序列都被合并为一个新序列。

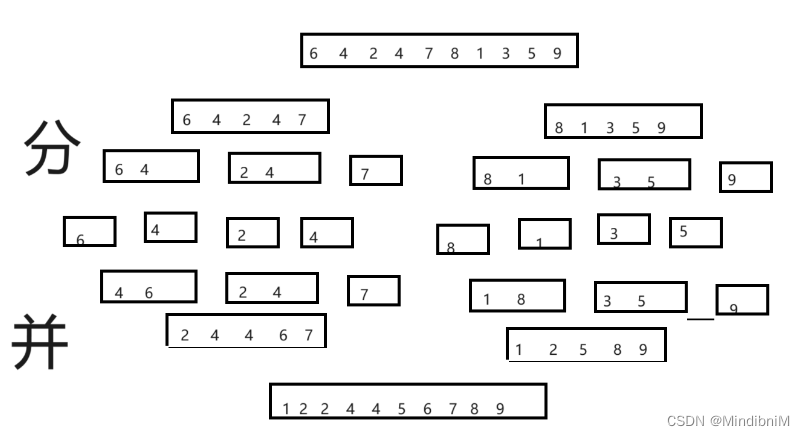一个简单的归并

二.实现

1.递归实现

void _Merge(int* a, int* temp, int left, int right)//归并递归
{
	if (left >= right)
		return;
	int mid = (right + left) / 2;
	_Merge(a, temp, left, mid);
	_Merge(a, temp, mid+1, right);
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int cout = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			temp[cout++] = a[begin1];
			begin1++;
		}
		else
		{
			temp[cout++] = a[begin2];
			begin2++;
		}
	}
	while (begin1 <= end1)
	{
		temp[cout++] = a[begin1];
		begin1++;
	}
	while (begin2 <= end2)
	{
		temp[cout++] = a[begin2];
		begin2++;
	}
	memcpy(a+left, temp+left, (right - left + 1) * sizeof(int));
}
void MergeSort(int* a, int n)//归并
{
	int* temp = (int*)malloc(n * sizeof(int));
	assert(temp);
	_Merge(a, temp, 0, n-1);
	free(temp);
}

将每一段分到有序.再合并两个有序序列,从最小系列向上合并

注意temp数组拷贝回去的位置,

2.非递归

void MergeNonRSort(int* a, int n)//归并排序非递归
{
	int* temp = (int*)malloc(n * sizeof(int));
	assert(temp);
	int gap = 1;
	while(gap<n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int cout = i;
			if (begin2 >= n)
				break;
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					temp[cout++] = a[begin1];
					begin1++;
				}
				else
				{
					temp[cout++] = a[begin2];
					begin2++;
				}
			}
			while (begin1 <= end1)
			{
				temp[cout++] = a[begin1];
				begin1++;
			}
			while (begin2 <= end2)
			{
				temp[cout++] = a[begin2];
				begin2++;
			}
			memcpy(a + i, temp + i, (end2-i+1) * sizeof(int));
		}
		gap *= 2;
	}
	free(temp);
}

gap表示每一有序序列的元素个数,从最小的1个元素开始合并,两两合并

注意边界的取值,当第二个序列全越界,便需要再合并,只越界end就修正边界值

三.特点

1.优势:

1. 稳定性： 归并排序是一种稳定的排序算法，即对于具有相等键值的元素，其相对顺序在排序后保持不变。

2. 用于文件： 归并排序在对硬盘内的数据进行排序更方便,和其他排序结合可很好的对文件排序

2,缺点:

1. 额外空间需求： 归并排序需要额外的内存空间来存储中间结果，这使得它在处理大规模数据时的空间复杂度较高。对于内存受限的环境，这可能是一个显著的缺点。

2. 不适合小规模数据： 对于小规模的数据集，归并排序的性能可能不如一些简单的排序算法，