递归
文章目录
- 递归
- 1.递归应用场景
- 2.递归的概念
- 3.递归调用机制
- 4.递归能解决什么问题
- 5.递归需要遵守的重要规则
- 6.递归-迷宫、八皇后问题
- 6.1 迷宫问题
- 6.2 八皇后问题
1.递归应用场景
迷宫问题(回溯),递归(Recursion)
2.递归的概念
简单的说:递归就是方法自己调用自己,每次调用时传入不同的变量。递归有助于编程者解决复杂的问题,同时可以让代码变得更简洁。
3.递归调用机制
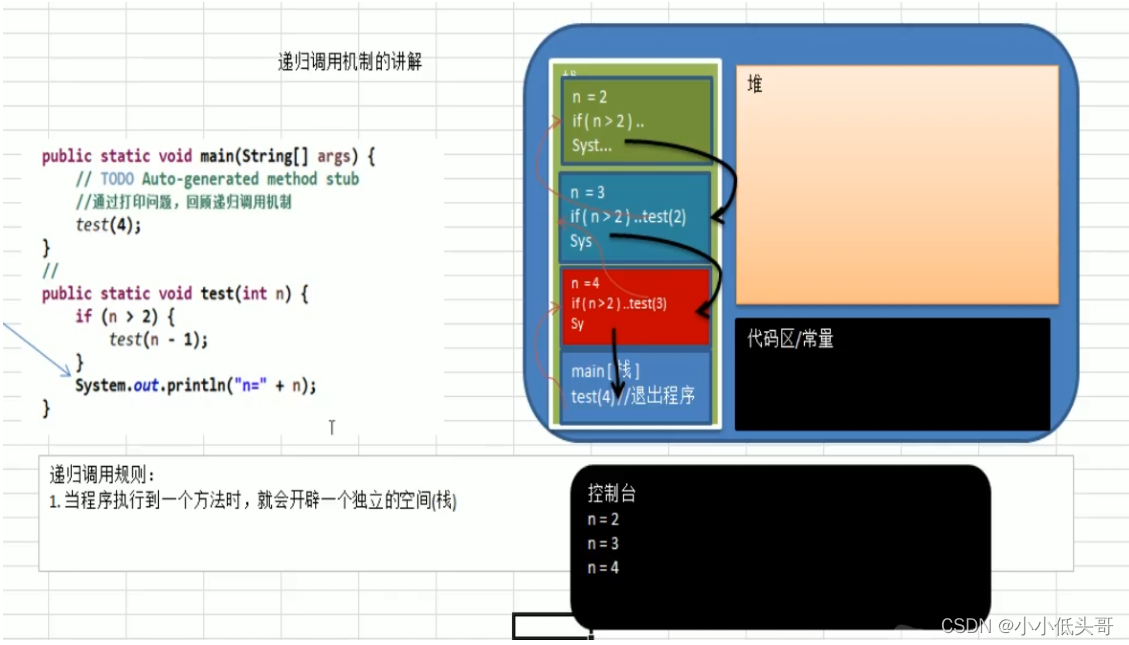
4.递归能解决什么问题
- 各种数学问题:8皇后问题,汉诺塔,阶乘问题,迷宫问题,球和篮子的问题
- 各种算法中也会使用到递归,比如快排,归并排序,二分查找,分治算法等
- 将用栈解决的问题–>递归代码比较简洁
5.递归需要遵守的重要规则
- 执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
- 方法的局部变量是独立的,不会相互影响
- 如果方法中使用的是引用类型变量(比如数组,类),就会共享该引用类型的数据。
- 递归必须向退出递归的条件逼近,否则就是无限递归,出现StackOverflowError。
- 当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
6.递归-迷宫、八皇后问题
6.1 迷宫问题

之前学韩老师java基础课的时候教过了这个迷宫问题,自己尝试先写了一下,发现还可以
package com.atguigu.recursion;
/**
* @author 小小低头哥
* @version 1.0
* 使用递归解决迷宫回溯问题
*/
public class Maze {
private static final int ROW = 7; //行
private static final int COL = 8; //列
private static final int BARRIER = 10; //障碍数
private static final int START_ROW = 0; //出生点的行
private static final int START_COL = 0; //出生点的列
private static final int END_ROW = ROW - 1; //终点的行
private static final int END_COL = COL - 1; //终点的列
public static void main(String[] args) {
maze();
}
public static void maze(){
//先创建一个二维数组
int[][] maze = new int[ROW][COL];
//0表示没走过 1表示走过且走得通 2表示走过行不通 3表示障碍 4表示终点
System.out.println("迷宫如下:");
for (int i = 0; i < ROW; i++) {
for (int j = 0; j < COL; j++) {
System.out.print(maze[i][j] + " ");
}
System.out.println();
}
//随机加入障碍
for (int i = 0; i < BARRIER; i++) {
maze[(int) (Math.random() * ROW)][(int) (Math.random() * COL)] = 3;
}
maze[START_ROW][START_COL] = 0; //出生点必须为0 防止随机赋值为3
maze[END_ROW][END_COL] = 4; //终点必须为4 防止随机赋值为3
System.out.println("加入障碍后的迷宫如下:");
for (int i = 0; i < ROW; i++) {
for (int j = 0; j < COL; j++) {
System.out.print(maze[i][j] + " ");
}
System.out.println();
}
if (en(maze, START_ROW, START_COL)) {
System.out.println("结束后的迷宫如下:");
for (int i = 0; i < ROW; i++) {
for (int j = 0; j < COL; j++) {
System.out.print(maze[i][j] + " ");
}
System.out.println();
}
}
}
/**
* @param maze 数组的状态
* @param nowRow 当前所在迷宫的行
* @param nowCol 当前所在迷宫的列
*/
public static boolean en(int[][] maze, int nowRow, int nowCol) { //出迷宫
if (nowRow > ROW - 1 || nowCol > COL - 1 || nowRow < 0 || nowCol < 0) { //说明越界了
return false;
}
if (maze[nowRow][nowCol] == 4) { //如果到达了终点 或者nowRow = END_ROW nowCol = END_COL
return true; //行得通
} else if (maze[nowRow][nowCol] == 3) { //说明走到了障碍
maze[nowRow][nowCol] = 2; //走过行不通
return false; //行不通
} else if (maze[nowRow][nowCol] == 2) {
return false; //行不通
} else if (maze[nowRow][nowCol] == 1) { //走过的路就不再走了
return false; //行不通
} else {
maze[nowRow][nowCol] = 1; //设为走过行得通
System.out.println("行:" + nowRow + "列" + nowCol);
//先向右走
if (en(maze, nowRow + 1, nowCol)) { //向下行得通的话
return true;
} else if (en(maze, nowRow, nowCol + 1)) {//向右走行得通的话
return true;
} else if (en(maze, nowRow, nowCol - 1)) { //向左走
return true;
} else if (en(maze, nowRow - 1, nowCol)) { //向上走
return true;
} else {
return false; //说明死路一条 无路可走
}
}
}
}
老韩写的如下
public static void main(String[] args) {
miGong();
}
public static void miGong(){
//先创建一个二维数组 模拟迷宫
//地图
int[][] map = new int[8][7];
//使用1 表示墙
//上下全部置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//设置挡板 1表示
map[3][1] = 1;
map[3][2] = 1;
//输出地图
System.out.println("地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
setWay(map,1,1);//给小秋找路
System.out.println("小球走过 并标识过地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
/**
* 使用递归回溯来给小球找路
* 说明: 1.map表示地图
* 2. i,j表示从地图那个位置开始走
* 3. 如果小球能到map[6][5]位置,则说明通路找到
* 4. 约定:当map[i][j]为0表示该点没有走过 当为1表示墙 2表示通路可走 3表示已经走过,但是走不通
* 5. 走迷宫时 下->右->上—>左,如果该点走不通 再回溯
* @param map 表示地图
* @param i 从哪个位置开始找
* @param j
* @return 找到就返回true 否则返回false
*/
public static boolean setWay(int[][] map,int i,int j){
if(map[6][5] == 2){ //同路已经找到
return true;
}else {
if(map[i][j]==0){ //如果当前这个点还没有走过
//按照策略 下->右->上->左
map[i][j] = 2; //假定该点可以走通
if(setWay(map,i+1,j)){ //向下走
return true;
}else if(setWay(map,i,j+1)){ //右
return true;
}else if(setWay(map,i-1,j)){ //上
return true;
}else if(setWay(map,i,j-1)){ //左
return true;
}else {
//说明该点走不通 是死路
map[i][j] = 3;
return false;
}
}else { //如果map[i][j] != 0,也可能是1,2,3
return false;
}
}
}
6.2 八皇后问题
同样在java基础时有过了解,这次能自己独立写出来,也是很欣慰的。俺的代码如下
package com.atguigu.recursion;
/**
* @author 小小低头哥
* @version 1.0
* 递归解决八皇后问题
*/
public class Queen {
private static final int SIZE = 8; //棋盘的大小 SIZE * SIZE
//先创建一个一维数组 用来记录每一列皇后所在的位置
private static int[] position = new int[SIZE];
private static int count = 0;//记录下有多少种情况
public static void main(String[] args) {
queen(0);
System.out.println("总共右count=" + count + "方法");
}
public static boolean queen(int n) { //判断第n个皇后的SIZE个位置
for (int i = 0; i < SIZE; i++) { //此皇后从摆放的第0行开始摆放
if (en(position, n, i)) { //如果第n个皇后可以放置在第i个位置
position[n] = i; //将此皇后的设置为i
if (n == SIZE - 1) { //成功找到一种方式
count++;
for (int j = 0; j < position.length; j++) {
System.out.print(position[j] + " ");
}
System.out.println();
continue; //直接进行下一个循环
}
queen(n + 1); //从下一个皇后继续判断
}
}
//退出循环 说明八个位置都判断完毕
return false;
}
/**
* 用来判断所摆的第n个皇后是否符合规定
*
* @param position 已经摆好的皇后位置的数组
* @param n 第n个皇后
* @param k 第n个皇后的位置
* @return
*/
public static boolean en(int[] position, int n, int k) {
for (int i = 0; i < n; i++) {
if (k == position[i]) { //表示同一行
return false;
} else if (position[i] + (n - i) == k || position[i] - (n - i) == k) { //表示在一个斜线上
return false;
}
}
//如果退出循环 说明第n个皇后摆放的位置对前面每一个皇后的位置都符号规定 返回true
return true;
}
}


韩老师代码如下
private static int count = 0;//记录下有多少种情况
public static void main(String[] args) {
new Queen().check(0);
System.out.println("一共有count=" + count + "解法");
}
//编写一个方法 放置第n个皇后
private void check(int n) {
if (n == max) { //说明皇后已经放好了
print();
count++;
return;
}
//依次放入皇后 并判断是否冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后,放入到该行的第一列
array[n] = i;
//判断方放置第n个皇后是否冲突
if (judge(n)) {
//接下来判断第n+1个皇后
check(n + 1);
}
//如果冲突继续循环 直到完成八个位置的循环摆放
}
}
//查看当放置第n个皇后 就去检测该皇后是否和前面已经摆放的皇后冲突
private boolean judge(int n) {
for (int i = 0; i < n; i++) {
//说明
//1. array[i] = array[n] 表示判断第n个皇后是否和前面的n-1个皇后同一列
//2. Math.abs(n - i) == Math.abs(array[n] - array[i])表示是否是同一列
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
//写一个方法 可以将皇后摆放的位置输出
private void print() {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}