1.为什么要引入光线追踪

光栅化阶段有些全局效果做的并不好，首先不太好做软阴影，然后是类镜面反射，表面很光滑但是又达不到镜面反射那么光滑，光线反射到这类物体上之后会经过好几次反射，其次是间接光照，光照从窗户中照射进来，会经历过很多次反射，这些在光栅化的时候都不好做

2.光栅化和光追的区别

① 光栅化：fast，但是质量不好

    光追： accurate（准确）, but is very slow

②光栅化：real-time

    光追：offline

光线追踪是一个质量非常高的方法，是完完全全符合物理规律的，这也是我们必须学习它的一个重要原因

3.Basic Ray-Tracing Algorithm

3.1.定义光线

（1）沿直线传播

（2）光线与光线间不会碰撞

（3）光线肯定从光源发出，进入场景不断弹射，最后进入人眼

//光线追踪用了光线的一个性质-reversal - reciprocity 光线的可逆性：可以理解为，光从光源发出不断弹射，最后进入人眼，也可以eyes可以发出一些感知的光线，打到物体上，最后打到光源（逆过程）。

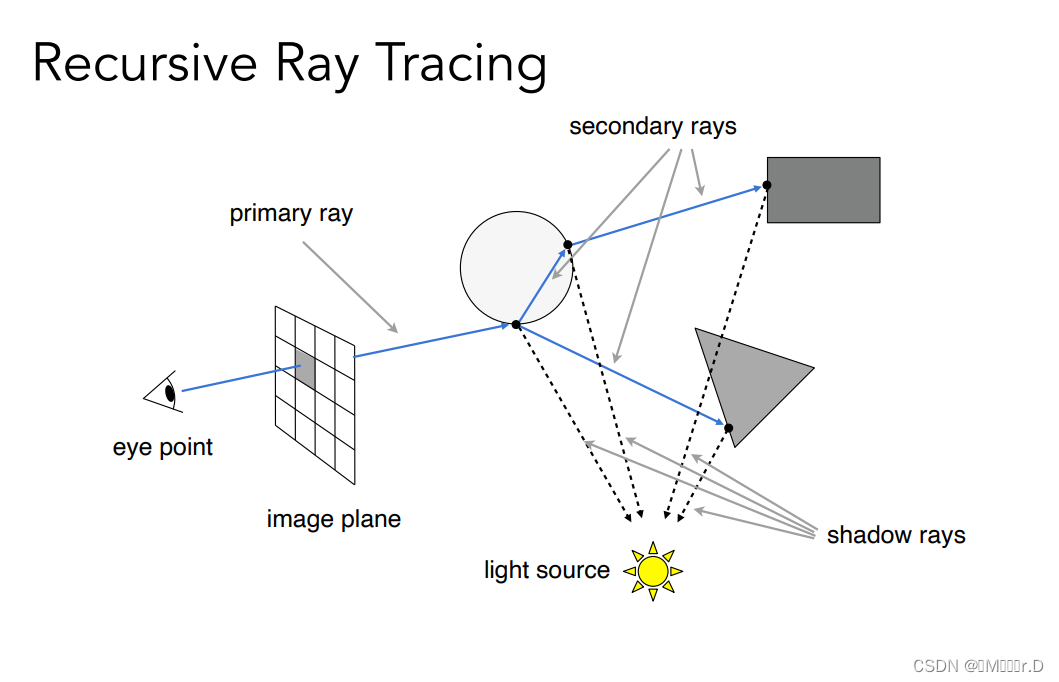
3.2.Ray Casting 光线投射

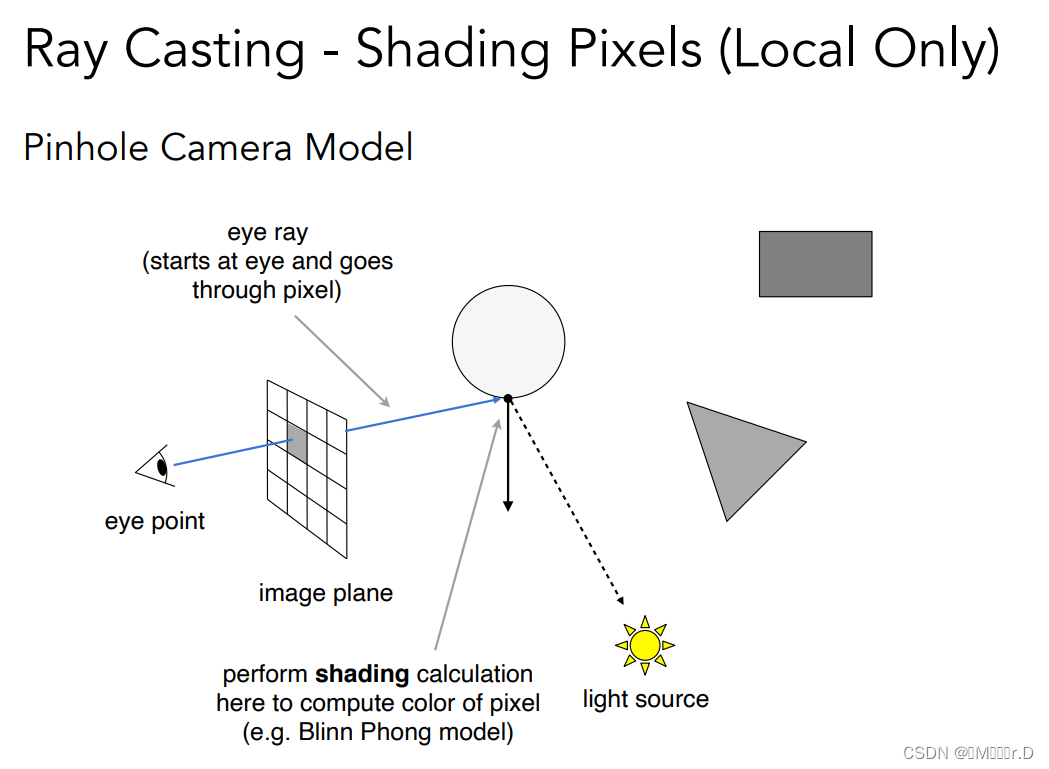
成像平面划为不同的pixel/格子，对于每一个pixel，从camera连一条线，穿过这个piexl，打出一根光线，一定会打到场景中的某个位置/或者和什么都不相交。

如果和某个物体相交，就是说沿着这个方向看，看到了哪儿，再与光源做连线（判断是否在shadow中），不在的话也就是光源可以看到这个点→就形成了一条有效的光路（光源→点→eyes）。接着就可以对这个点进行着色计算

这里假设人眼是一个针孔相机，也就是一个点，光源是一个点光源，场景中的物体，光线打到后会发生完美的反射/折射

3.3.Recursive (Whitted-Style) Ray Tracing

前面的场景中光线只弹射了一次，但实际上光线可以在场景中弹射多次，Recursive (Whitted-Style) Ray Tracing实现了这种情况，采用了递归的思想。

①在任意一点可以继续传播，只需要正确的计算折射，反射的方向，当然要考虑到光照能量的衰减

②着色也会影响，每个弹射点都会计算着色（连到光源），所有着色都加到pixel中

4.光线与表面交点的计算

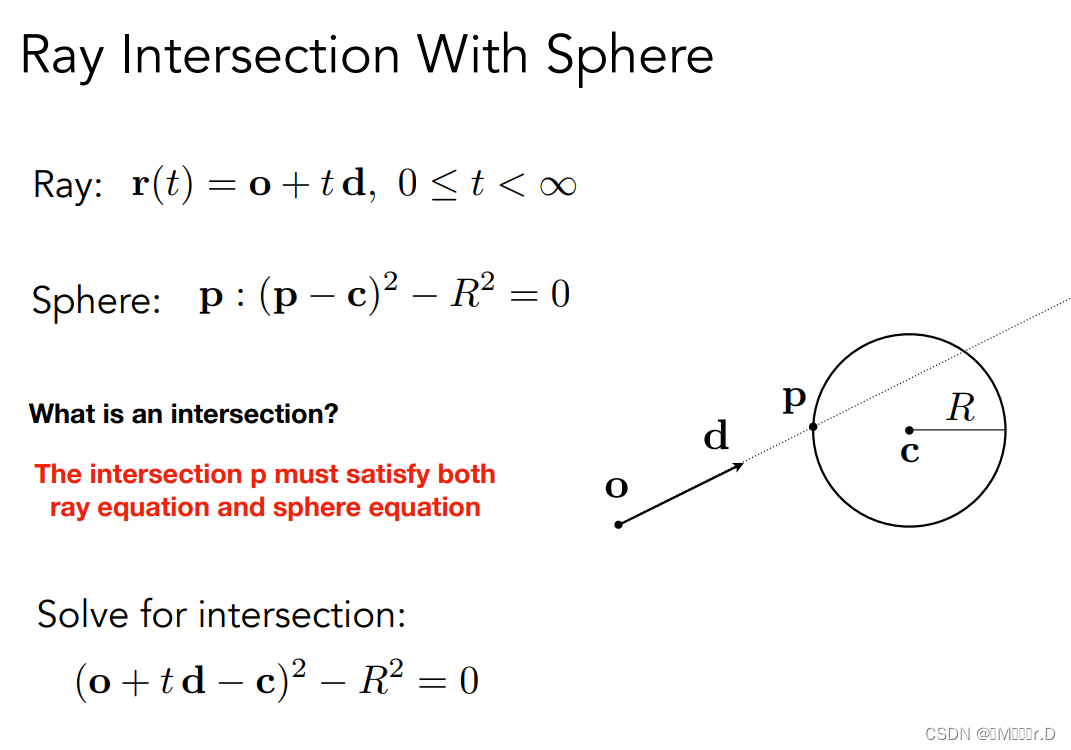
4.1.定义光射线

o是光源的位置，d是光线射出的方向，t可以认为是时间

4.2.求光和球的交点

交点必然同时满足两个方程，联立方程组就可以解出

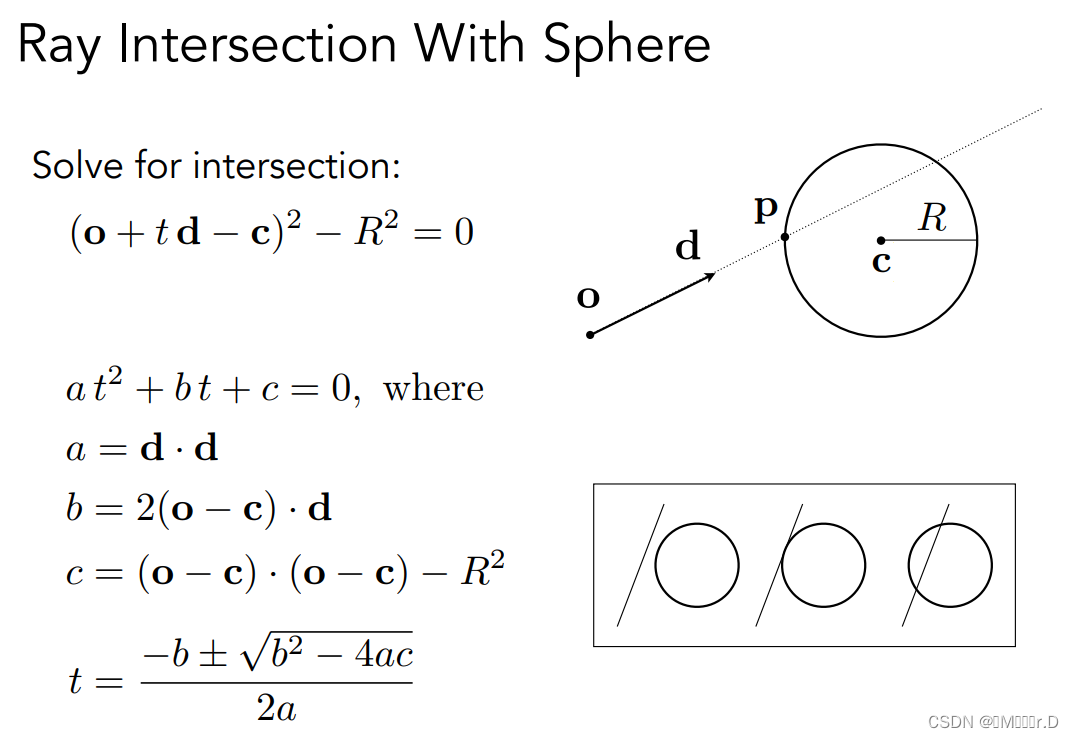
4.3.和隐式表面的交点

可以类比和球的交点，原理差不多

t需满足：①是实数 ② 是正的

4.4.和显式表面（一个重要的：三角形）的交点

通过光线与三角形求交，我们还可以判断光源在网格内还是外：从光源出发一条射线，如果能穿过网格两次，那么它一定在网格外，而如果只穿过一次，那就说明它在网格内，当然前提是网格是封闭的。（不是很懂）

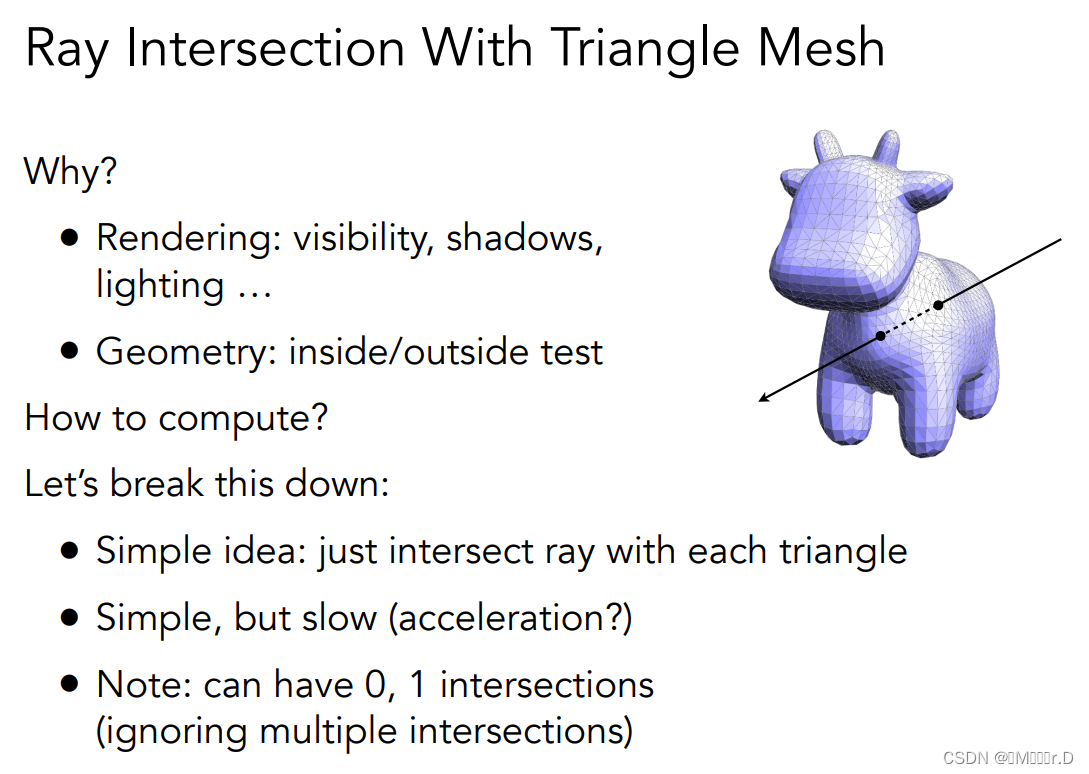
4.4.1.一般求解算法

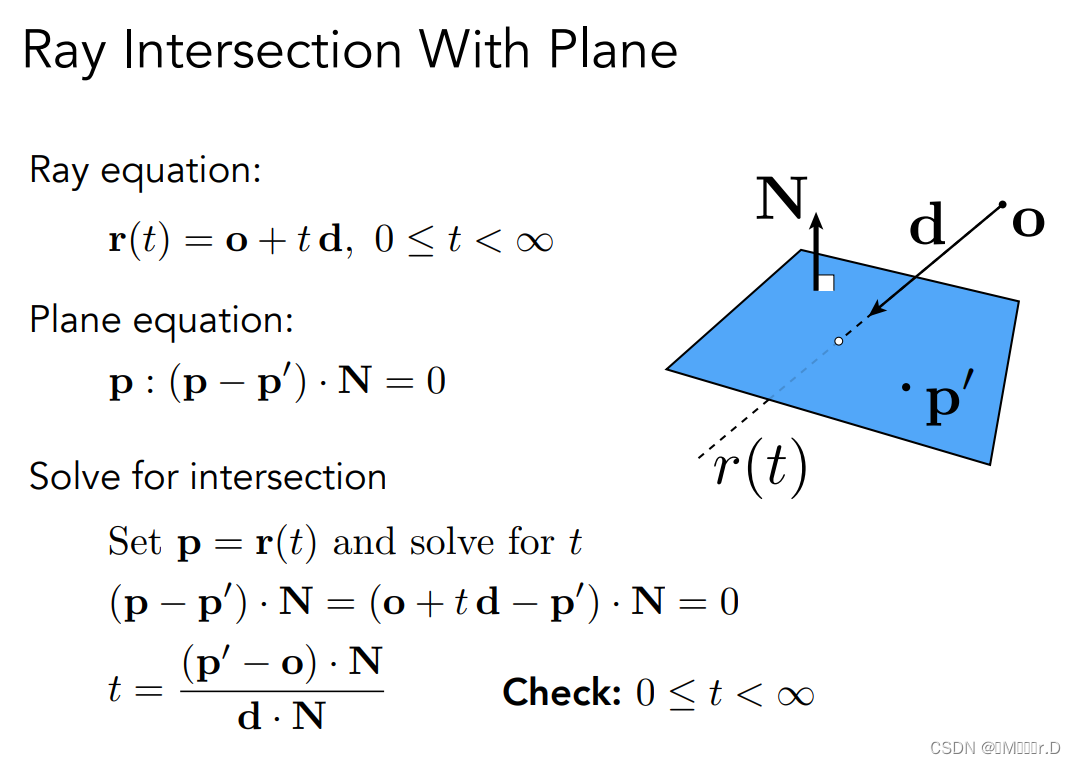
首先，三角形一定在一个平面内，因为三个点确定一个平面。于是人们想到了一种方法，先做光线与平面求交，得到交点之后再判断交点在不在三角形内。而点在三角形内的判断我们之前光栅化那篇已经讲过了。（通过叉乘计算）

平面通过平面法线和平面上一点可以确定，交点必定同时满足光线和平面的公式，联立方程解出来t之后判断是否在三角形内

4.4.2Möller Trumbore算法

Möller Trumbore算法是一种更为快速的计算光线与三角形求交的算法，它没有分为两个步骤，而是直接计算光线是否与三角形有交点。这个算法用到了重心坐标，也就是说把三角形面上的点用重心坐标表示然后和光线方程联立求解，而每个坐标恰好又是三个分量x，y，z，我们需要求解的也是三个未知量t，b1，b2，三个分量分别可以构建出一个方程，三个未知量三个方程组，我们用克莱姆法则很容易求解。而求解得出的t，同样需要大于0，那么如何判断求出的点是否在三角形内呢？我们前面讲重心坐标的时候讲到过，如果一个点在三角形内，那么它重心坐标下的三个分量都应该非负，也就是说b1，b2，1-b1-b2这三个量要≥0。

4.5.光线和表面求交的加速

4.5.1Bounding Volumes（包围盒/体积）

• 包围盒：一个物体可以用简单的形状包围起来，保证这个物体一定在这个简单的形状中。
• 一个重要逻辑：如果光线连包围盒都碰不到，就更不可能碰到物体。

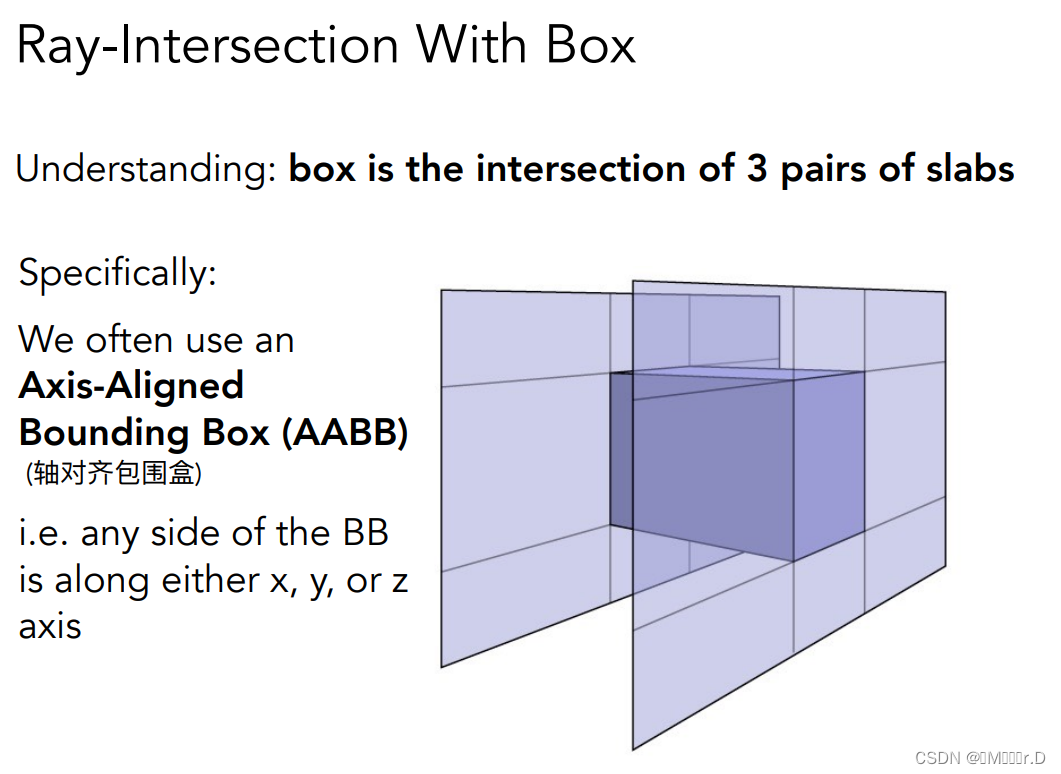
4.5.2对于3D物体最常用的包围盒：长方体

长方体可以理解成三个不同的对面（pair of slabs）形成的交集

在实际情况中我们经常用到的是轴对齐包围盒，意思就是说这个包围盒的6个面都是和三维空间的坐标轴对齐的，它们分别和XOY,YOZ,XOZ平面平行。这样做的目的是方便后面的计算。

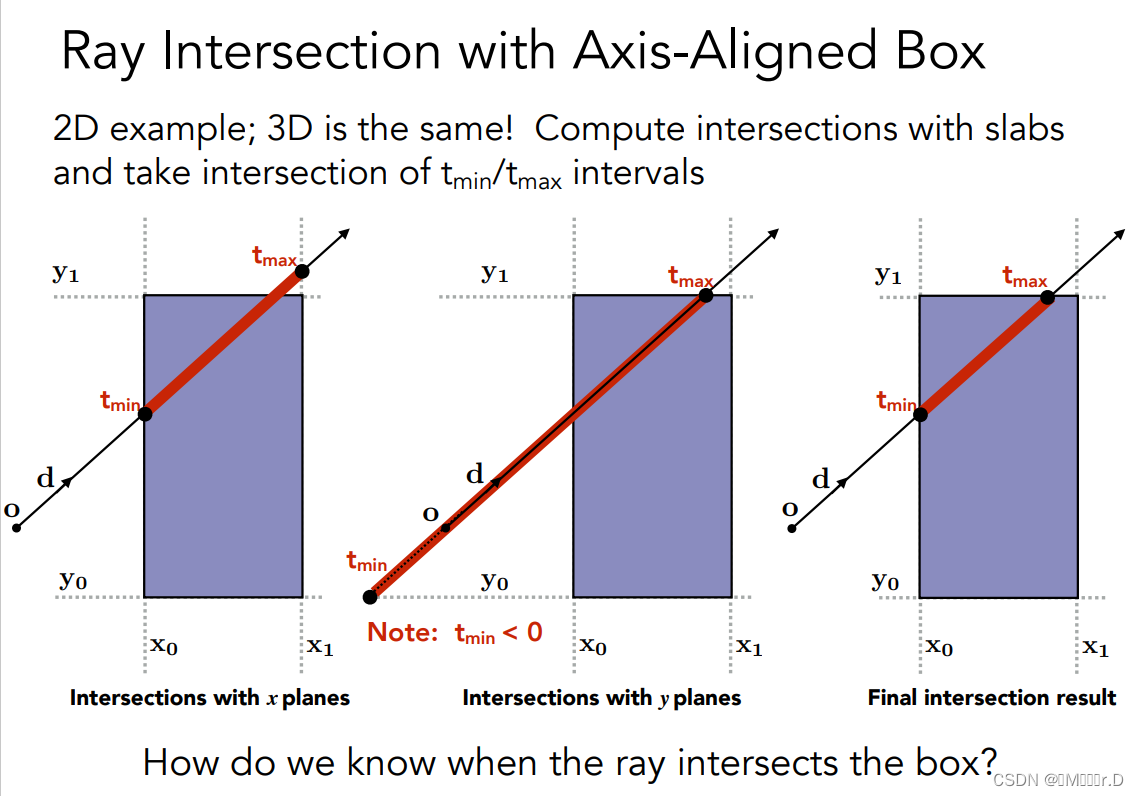
4.5.3二维情况举例

用光线o+td先和包围盒的与y轴平行的x0和x1面求交，我们可以得到光线进入到达x0的时间tmin，从x1出去的时间tmax，同样的我们对y0，y1两个面做同样的运算也可以得到两个t值，那么光线在包围盒中的是那一段呢？显然我们对左，中两幅图求交就是最右面的图，也就是光线进入包围盒和出去包围盒的时间。为什么会这样呢？我们说，轴对齐包围盒本身就是坐标轴的面求交得到的一个空间，那么光线在这片空间中的时间自然也就是进出各个面的光线时间求交。

4.5.4三维空间的情况

就是多了一个面的进出时间计算，当光线进入了所有的面，就说明光线进入了盒子，而光线离开任意一个面，就说明光线离开了盒子。所以光线进入盒子的时间就是光线进入三个面时间中的最大值，而光线离开盒子的时间就是光线离开三个面时间中的最小值。而如果求出的进入盒子时间<离开盒子时间，也就说明光线在盒子里面待了一段时间，也就是和包围盒有交点

总结：
负的情况：t离开<0 →Box在光背后

光线起点在Box内 ：t离开≥0 ＆ t进入 <0 

iff（当且仅当）t离开 < t进入 ＆＆ t离开≥0 时，有交点