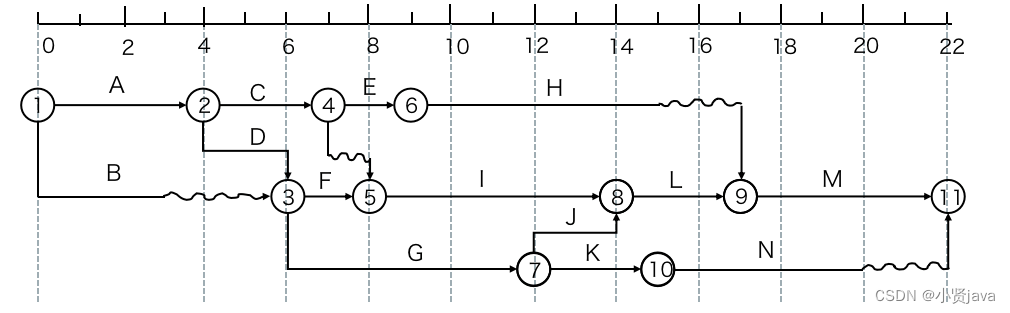
class067 二维动态规划【算法】

news2024/11/20 9:18:47

class067 二维动态规划

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

code1 64. 最小路径和

// 最小路径和
// 给定一个包含非负整数的 m x n 网格 grid
// 请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
// 说明：每次只能向下或者向右移动一步。
// 测试链接 : https://leetcode.cn/problems/minimum-path-sum/

dp[i][j]：从(0,0)到(i,j)最小路径 和
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]

第0行：dp[0][j-1]+grid[0][j]
第0列：dp[i-1][0]+grid[i-1][0]

code1 暴力递归
code2 记忆化搜索
code3 动态规划
code4 空间压缩

package class067;

// 最小路径和
// 给定一个包含非负整数的 m x n 网格 grid
// 请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
// 说明：每次只能向下或者向右移动一步。
// 测试链接 : https://leetcode.cn/problems/minimum-path-sum/
public class Code01_MinimumPathSum {

	// 暴力递归
	public static int minPathSum1(int[][] grid) {
		return f1(grid, grid.length - 1, grid[0].length - 1);
	}

	// 从(0,0)到(i,j)最小路径和
	// 一定每次只能向右或者向下
	public static int f1(int[][] grid, int i, int j) {
		if (i == 0 && j == 0) {
			return grid[0][0];
		}
		int up = Integer.MAX_VALUE;
		int left = Integer.MAX_VALUE;
		if (i - 1 >= 0) {
			up = f1(grid, i - 1, j);
		}
		if (j - 1 >= 0) {
			left = f1(grid, i, j - 1);
		}
		return grid[i][j] + Math.min(up, left);
	}

	// 记忆化搜索
	public static int minPathSum2(int[][] grid) {
		int n = grid.length;
		int m = grid[0].length;
		int[][] dp = new int[n][m];
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				dp[i][j] = -1;
			}
		}
		return f2(grid, grid.length - 1, grid[0].length - 1, dp);
	}

	public static int f2(int[][] grid, int i, int j, int[][] dp) {
		if (dp[i][j] != -1) {
			return dp[i][j];
		}
		int ans;
		if (i == 0 && j == 0) {
			ans = grid[0][0];
		} else {
			int up = Integer.MAX_VALUE;
			int left = Integer.MAX_VALUE;
			if (i - 1 >= 0) {
				up = f2(grid, i - 1, j, dp);
			}
			if (j - 1 >= 0) {
				left = f2(grid, i, j - 1, dp);
			}
			ans = grid[i][j] + Math.min(up, left);
		}
		dp[i][j] = ans;
		return ans;
	}

	// 严格位置依赖的动态规划
	public static int minPathSum3(int[][] grid) {
		int n = grid.length;
		int m = grid[0].length;
		int[][] dp = new int[n][m];
		dp[0][0] = grid[0][0];
		for (int i = 1; i < n; i++) {
			dp[i][0] = dp[i - 1][0] + grid[i][0];
		}
		for (int j = 1; j < m; j++) {
			dp[0][j] = dp[0][j - 1] + grid[0][j];
		}
		for (int i = 1; i < n; i++) {
			for (int j = 1; j < m; j++) {
				dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
			}
		}
		return dp[n - 1][m - 1];
	}

	// 严格位置依赖的动态规划 + 空间压缩技巧
	public static int minPathSum4(int[][] grid) {
		int n = grid.length;
		int m = grid[0].length;
		// 先让dp表，变成想象中的表的第0行的数据
		int[] dp = new int[m];
		dp[0] = grid[0][0];
		for (int j = 1; j < m; j++) {
			dp[j] = dp[j - 1] + grid[0][j];
		}
		for (int i = 1; i < n; i++) {
			// i = 1，dp表变成想象中二维表的第1行的数据
			// i = 2，dp表变成想象中二维表的第2行的数据
			// i = 3，dp表变成想象中二维表的第3行的数据
			// ...
			// i = n-1，dp表变成想象中二维表的第n-1行的数据
			dp[0] += grid[i][0];
			for (int j = 1; j < m; j++) {
				dp[j] = Math.min(dp[j - 1], dp[j]) + grid[i][j];
			}
		}
		return dp[m - 1];
	}

}

code2 79. 单词搜索

// 单词搜索（无法改成动态规划）
// 给定一个 m x n 二维字符网格 board 和一个字符串单词 word
// 如果 word 存在于网格中，返回 true ；否则，返回 false 。
// 单词必须按照字母顺序，通过相邻的单元格内的字母构成
// 其中"相邻"单元格是那些水平相邻或垂直相邻的单元格
// 同一个单元格内的字母不允许被重复使用
// 测试链接 : https://leetcode.cn/problems/word-search/

code 递归

package class067;

// 单词搜索（无法改成动态规划）
// 给定一个 m x n 二维字符网格 board 和一个字符串单词 word
// 如果 word 存在于网格中，返回 true ；否则，返回 false 。
// 单词必须按照字母顺序，通过相邻的单元格内的字母构成
// 其中"相邻"单元格是那些水平相邻或垂直相邻的单元格
// 同一个单元格内的字母不允许被重复使用
// 测试链接 : https://leetcode.cn/problems/word-search/
public class Code02_WordSearch {

	public static boolean exist(char[][] board, String word) {
		char[] w = word.toCharArray();
		for (int i = 0; i < board.length; i++) {
			for (int j = 0; j < board[0].length; j++) {
				if (f(board, i, j, w, 0)) {
					return true;
				}
			}
		}
		return false;
	}

	// 因为board会改其中的字符
	// 用来标记哪些字符无法再用
	// 带路径的递归无法改成动态规划或者说没必要
	// 从(i,j)出发，来到w[k]，请问后续能不能把word走出来w[k...]
	public static boolean f(char[][] b, int i, int j, char[] w, int k) {
		if (k == w.length) {
			return true;
		}
		if (i < 0 || i == b.length || j < 0 || j == b[0].length || b[i][j] != w[k]) {
			return false;
		}
		// 不越界，b[i][j] == w[k]
		char tmp = b[i][j];
		b[i][j] = 0;
		boolean ans = f(b, i - 1, j, w, k + 1) 
				|| f(b, i + 1, j, w, k + 1) 
				|| f(b, i, j - 1, w, k + 1)
				|| f(b, i, j + 1, w, k + 1);
		b[i][j] = tmp;
		return ans;
	}

}

code3 1143. 最长公共子序列

// 最长公共子序列
// 给定两个字符串text1和text2
// 返回这两个字符串的最长 公共子序列 的长度
// 如果不存在公共子序列，返回0
// 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列
// 测试链接 : https://leetcode.cn/problems/longest-common-subsequence/

dp[i][j]：text1[前i个]和text2[前j个]最长公共子序列的长度
dp[i-1][j-1]+1,text1[i-1]==text2[j-1]
max(dp[i-1][j],dp[i][j-1])

第0行 ：0
第0列： 0

code1 递归
code2 递归
code3 记忆化搜索
code4 动态规划
code5 空间压缩

package class067;

// 最长公共子序列
// 给定两个字符串text1和text2
// 返回这两个字符串的最长 公共子序列 的长度
// 如果不存在公共子序列，返回0
// 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列
// 测试链接 : https://leetcode.cn/problems/longest-common-subsequence/
public class Code03_LongestCommonSubsequence {

	public static int longestCommonSubsequence1(String str1, String str2) {
		char[] s1 = str1.toCharArray();
		char[] s2 = str2.toCharArray();
		int n = s1.length;
		int m = s2.length;
		return f1(s1, s2, n - 1, m - 1);
	}

	// s1[0....i1]与s2[0....i2]最长公共子序列长度
	public static int f1(char[] s1, char[] s2, int i1, int i2) {
		if (i1 < 0 || i2 < 0) {
			return 0;
		}
		int p1 = f1(s1, s2, i1 - 1, i2 - 1);
		int p2 = f1(s1, s2, i1 - 1, i2);
		int p3 = f1(s1, s2, i1, i2 - 1);
		int p4 = s1[i1] == s2[i2] ? (p1 + 1) : 0;
		return Math.max(Math.max(p1, p2), Math.max(p3, p4));
	}

	// 为了避免很多边界讨论
	// 很多时候往往不用下标来定义尝试，而是用长度来定义尝试
	// 因为长度最短是0，而下标越界的话讨论起来就比较麻烦
	public static int longestCommonSubsequence2(String str1, String str2) {
		char[] s1 = str1.toCharArray();
		char[] s2 = str2.toCharArray();
		int n = s1.length;
		int m = s2.length;
		return f2(s1, s2, n, m);
	}

	// s1[前缀长度为len1]对应s2[前缀长度为len2]
	// 最长公共子序列长度
	public static int f2(char[] s1, char[] s2, int len1, int len2) {
		if (len1 == 0 || len2 == 0) {
			return 0;
		}
		int ans;
		if (s1[len1 - 1] == s2[len2 - 1]) {
			ans = f2(s1, s2, len1 - 1, len2 - 1) + 1;
		} else {
			ans = Math.max(f2(s1, s2, len1 - 1, len2), f2(s1, s2, len1, len2 - 1));
		}
		return ans;
	}

	// 记忆化搜索
	public static int longestCommonSubsequence3(String str1, String str2) {
		char[] s1 = str1.toCharArray();
		char[] s2 = str2.toCharArray();
		int n = s1.length;
		int m = s2.length;
		int[][] dp = new int[n + 1][m + 1];
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= m; j++) {
				dp[i][j] = -1;
			}
		}
		return f3(s1, s2, n, m, dp);
	}

	public static int f3(char[] s1, char[] s2, int len1, int len2, int[][] dp) {
		if (len1 == 0 || len2 == 0) {
			return 0;
		}
		if (dp[len1][len2] != -1) {
			return dp[len1][len2];
		}
		int ans;
		if (s1[len1 - 1] == s2[len2 - 1]) {
			ans = f3(s1, s2, len1 - 1, len2 - 1, dp) + 1;
		} else {
			ans = Math.max(f3(s1, s2, len1 - 1, len2, dp), f3(s1, s2, len1, len2 - 1, dp));
		}
		dp[len1][len2] = ans;
		return ans;
	}

	// 严格位置依赖的动态规划
	public static int longestCommonSubsequence4(String str1, String str2) {
		char[] s1 = str1.toCharArray();
		char[] s2 = str2.toCharArray();
		int n = s1.length;
		int m = s2.length;
		int[][] dp = new int[n + 1][m + 1];
		for (int len1 = 1; len1 <= n; len1++) {
			for (int len2 = 1; len2 <= m; len2++) {
				if (s1[len1 - 1] == s2[len2 - 1]) {
					dp[len1][len2] = 1 + dp[len1 - 1][len2 - 1];
				} else {
					dp[len1][len2] = Math.max(dp[len1 - 1][len2], dp[len1][len2 - 1]);
				}
			}
		}
		return dp[n][m];
	}

	// 严格位置依赖的动态规划 + 空间压缩
	public static int longestCommonSubsequence5(String str1, String str2) {
		char[] s1, s2;
		if (str1.length() >= str2.length()) {
			s1 = str1.toCharArray();
			s2 = str2.toCharArray();
		} else {
			s1 = str2.toCharArray();
			s2 = str1.toCharArray();
		}
		int n = s1.length;
		int m = s2.length;
		int[] dp = new int[m + 1];
		for (int len1 = 1; len1 <= n; len1++) {
			int leftUp = 0, backup;
			for (int len2 = 1; len2 <= m; len2++) {
				backup = dp[len2];
				if (s1[len1 - 1] == s2[len2 - 1]) {
					dp[len2] = 1 + leftUp;
				} else {
					dp[len2] = Math.max(dp[len2], dp[len2 - 1]);
				}
				leftUp = backup;
			}
		}
		return dp[m];
	}

}

code4 516. 最长回文子序列

// 最长回文子序列
// 给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度
// 测试链接 : https://leetcode.cn/problems/longest-palindromic-subsequence/

dp[i][j]：从[i,j]字符中有最长回文子序列的长度
1,i=j
1/2,s[i]==s[j],i+1=j
2+dp[i+1][j-1],s[i]==s[j]
max(dp[i+1][j],dp[i][j-1])

从左到右，从下到上

code1 递归
code2 记忆化搜索
code3 动态规划
code4 空间压缩

package class067;

// 最长回文子序列
// 给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度
// 测试链接 : https://leetcode.cn/problems/longest-palindromic-subsequence/
public class Code04_LongestPalindromicSubsequence {

	// 最长回文子序列问题可以转化成最长公共子序列问题
	// 不过这里讲述区间动态规划的思路
	// 区间dp还会有单独的视频做详细讲述
	public static int longestPalindromeSubseq1(String str) {
		char[] s = str.toCharArray();
		int n = s.length;
		return f1(s, 0, n - 1);
	}

	// s[l...r]最长回文子序列长度
	// l <= r
	public static int f1(char[] s, int l, int r) {
		if (l == r) {
			return 1;
		}
		if (l + 1 == r) {
			return s[l] == s[r] ? 2 : 1;
		}
		if (s[l] == s[r]) {
			return 2 + f1(s, l + 1, r - 1);
		} else {
			return Math.max(f1(s, l + 1, r), f1(s, l, r - 1));
		}
	}

	public static int longestPalindromeSubseq2(String str) {
		char[] s = str.toCharArray();
		int n = s.length;
		int[][] dp = new int[n][n];
		return f2(s, 0, n - 1, dp);
	}

	public static int f2(char[] s, int l, int r, int[][] dp) {
		if (l == r) {
			return 1;
		}
		if (l + 1 == r) {
			return s[l] == s[r] ? 2 : 1;
		}
		if (dp[l][r] != 0) {
			return dp[l][r];
		}
		int ans;
		if (s[l] == s[r]) {
			ans = 2 + f2(s, l + 1, r - 1, dp);
		} else {
			ans = Math.max(f2(s, l + 1, r, dp), f2(s, l, r - 1, dp));
		}
		dp[l][r] = ans;
		return ans;
	}

	public static int longestPalindromeSubseq3(String str) {
		char[] s = str.toCharArray();
		int n = s.length;
		int[][] dp = new int[n][n];
		for (int l = n - 1; l >= 0; l--) {
			dp[l][l] = 1;
			if (l + 1 < n) {
				dp[l][l + 1] = s[l] == s[l + 1] ? 2 : 1;
			}
			for (int r = l + 2; r < n; r++) {
				if (s[l] == s[r]) {
					dp[l][r] = 2 + dp[l + 1][r - 1];
				} else {
					dp[l][r] = Math.max(dp[l + 1][r], dp[l][r - 1]);
				}
			}
		}
		return dp[0][n - 1];
	}

	public static int longestPalindromeSubseq4(String str) {
		char[] s = str.toCharArray();
		int n = s.length;
		int[] dp = new int[n];
		for (int l = n - 1, leftDown = 0, backup; l >= 0; l--) {
			// dp[l] : 想象中的dp[l][l]
			dp[l] = 1;
			if (l + 1 < n) {
				leftDown = dp[l + 1];
				// dp[l+1] : 想象中的dp[l][l+1]
				dp[l + 1] = s[l] == s[l + 1] ? 2 : 1;
			}
			for (int r = l + 2; r < n; r++) {
				backup = dp[r];
				if (s[l] == s[r]) {
					dp[r] = 2 + leftDown;
				} else {
					dp[r] = Math.max(dp[r], dp[r - 1]);
				}
				leftDown = backup;
			}
		}
		return dp[n - 1];
	}

}

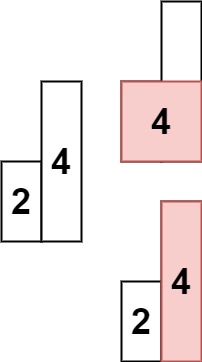
code5 节点数为n高度不大于m的二叉树个数

// 节点数为n高度不大于m的二叉树个数
// 现在有n个节点，计算出有多少个不同结构的二叉树
// 满足节点个数为n且树的高度不超过m的方案
// 因为答案很大，所以答案需要模上1000000007后输出
// 测试链接 : https://www.nowcoder.com/practice/aaefe5896cce4204b276e213e725f3ea
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下所有代码，把主类名改成Main，可以直接通过

思路：就是头占1个，左右占[0,n-1]
dp[i][j]：节点数为i高度不大于j的二叉树个数
∑dp[k][j-1]*dp[i-k-1][j-1],(0<=k<=i)

package class067;

// 节点数为n高度不大于m的二叉树个数
// 现在有n个节点，计算出有多少个不同结构的二叉树
// 满足节点个数为n且树的高度不超过m的方案
// 因为答案很大，所以答案需要模上1000000007后输出
// 测试链接 : https://www.nowcoder.com/practice/aaefe5896cce4204b276e213e725f3ea
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下所有代码，把主类名改成Main，可以直接通过

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Code05_NodenHeightNotLargerThanm {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		while (in.nextToken() != StreamTokenizer.TT_EOF) {
			int n = (int) in.nval;
			in.nextToken();
			int m = (int) in.nval;
			out.println(compute3(n, m));
		}
		out.flush();
		out.close();
		br.close();
	}

	public static int MAXN = 51;

	public static int MOD = 1000000007;

	// 记忆化搜索
	public static long[][] dp1 = new long[MAXN][MAXN];

	static {
		for (int i = 0; i < MAXN; i++) {
			for (int j = 0; j < MAXN; j++) {
				dp1[i][j] = -1;
			}
		}
	}

	// 二叉树节点数为n
	// 高度不能超过m
	// 结构数返回
	// 记忆化搜索
	public static int compute1(int n, int m) {
		if (n == 0) {
			return 1;
		}
		// n > 0
		if (m == 0) {
			return 0;
		}
		if (dp1[n][m] != -1) {
			return (int) dp1[n][m];
		}
		long ans = 0;
		// n个点，头占掉1个
		for (int k = 0; k < n; k++) {
			// 一共n个节点，头节点已经占用了1个名额
			// 如果左树占用k个，那么右树就占用i-k-1个
			ans = (ans + ((long) compute1(k, m - 1) * compute1(n - k - 1, m - 1)) % MOD) % MOD;
		}
		dp1[n][m] = ans;
		return (int) ans;
	}

	// 严格位置依赖的动态规划
	public static long[][] dp2 = new long[MAXN][MAXN];

	public static int compute2(int n, int m) {
		for (int j = 0; j <= m; j++) {
			dp2[0][j] = 1;
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				dp2[i][j] = 0;
				for (int k = 0; k < i; k++) {
					// 一共i个节点，头节点已经占用了1个名额
					// 如果左树占用k个，那么右树就占用i-k-1个
					dp2[i][j] = (dp2[i][j] + dp2[k][j - 1] * dp2[i - k - 1][j - 1] % MOD) % MOD;
				}
			}
		}
		return (int) dp2[n][m];
	}

	// 空间压缩
	public static long[] dp3 = new long[MAXN];

	public static int compute3(int n, int m) {
		dp3[0] = 1;
		for (int i = 1; i <= n; i++) {
			dp3[i] = 0;
		}
		for (int j = 1; j <= m; j++) {
			// 根据依赖，一定要先枚举列
			for (int i = n; i >= 1; i--) {
				// 再枚举行，而且i不需要到达0，i>=1即可
				dp3[i] = 0;
				for (int k = 0; k < i; k++) {
					// 枚举
					dp3[i] = (dp3[i] + dp3[k] * dp3[i - k - 1] % MOD) % MOD;
				}
			}
		}
		return (int) dp3[n];
	}

}

code6 329. 矩阵中的最长递增路径

// 矩阵中的最长递增路径
// 给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度
// 对于每个单元格，你可以往上，下，左，右四个方向移动
// 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）
// 测试链接 : https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/

dp[i][j]：从(i,j)出发到达的最长递增路径
max(dp[i-1][j],dp[i+1][j],dp[i][j-1],dp[i][j+1])+1,只有对应大才能走

code1 递归
code2 记忆化搜索

package class067;

// 矩阵中的最长递增路径
// 给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度
// 对于每个单元格，你可以往上，下，左，右四个方向移动
// 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）
// 测试链接 : https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/
public class Code06_LongestIncreasingPath {

	public static int longestIncreasingPath1(int[][] grid) {
		int ans = 0;
		for (int i = 0; i < grid.length; i++) {
			for (int j = 0; j < grid[0].length; j++) {
				ans = Math.max(ans, f1(grid, i, j));
			}
		}
		return ans;
	}

	// 从(i,j)出发，能走出来多长的递增路径，返回最长长度
	public static int f1(int[][] grid, int i, int j) {
		int next = 0;
		if (i > 0 && grid[i][j] < grid[i - 1][j]) {
			next = Math.max(next, f1(grid, i - 1, j));
		}
		if (i + 1 < grid.length && grid[i][j] < grid[i + 1][j]) {
			next = Math.max(next, f1(grid, i + 1, j));
		}
		if (j > 0 && grid[i][j] < grid[i][j - 1]) {
			next = Math.max(next, f1(grid, i, j - 1));
		}
		if (j + 1 < grid[0].length && grid[i][j] < grid[i][j + 1]) {
			next = Math.max(next, f1(grid, i, j + 1));
		}
		return next + 1;
	}

	public static int longestIncreasingPath2(int[][] grid) {
		int n = grid.length;
		int m = grid[0].length;
		int[][] dp = new int[n][m];
		int ans = 0;
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				ans = Math.max(ans, f2(grid, i, j, dp));
			}
		}
		return ans;
	}

	public static int f2(int[][] grid, int i, int j, int[][] dp) {
		if (dp[i][j] != 0) {
			return dp[i][j];
		}
		int next = 0;
		if (i > 0 && grid[i][j] < grid[i - 1][j]) {
			next = Math.max(next, f2(grid, i - 1, j, dp));
		}
		if (i + 1 < grid.length && grid[i][j] < grid[i + 1][j]) {
			next = Math.max(next, f2(grid, i + 1, j, dp));
		}
		if (j > 0 && grid[i][j] < grid[i][j - 1]) {
			next = Math.max(next, f2(grid, i, j - 1, dp));
		}
		if (j + 1 < grid[0].length && grid[i][j] < grid[i][j + 1]) {
			next = Math.max(next, f2(grid, i, j + 1, dp));
		}
		dp[i][j] = next + 1;
		return next + 1;
	}

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1297969.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【腾讯云 HAI域探秘】StableDiffusionWebUI 让我找到了宫崎骏动漫里的夏天

【腾讯云 HAI域探秘】StableDiffusionWebUI 让我找到了宫崎骏动漫里的夏天

目录 前言一、HAI二、应用场景三、构建 Stable Diffusion 模型1、新建HAI应用2、StableDiffusionWebUI&#xff08;1&#xff09;功能介绍&#xff08;2&#xff09;页面转中文&#xff08;3&#xff09;AI绘图① 正向提示词语② 反向提示词③ “” 、“ AND”、“|” 用法④ 权…
阅读更多...
网上下载的pdf文件，为什么不能复制文字？

网上下载的pdf文件，为什么不能复制文字？

不知道大家有没有到过这种情况&#xff1f;在网上下载的PDF文件打开之后&#xff0c;发现选中文字之后无法复制。甚至其他功能也都无法使用&#xff0c;这是怎么回事&#xff1f;该怎么办&#xff1f; 当我们发现文件打开之后&#xff0c;编辑功能无法使用&#xff0c;很可能是…
阅读更多...
基于MATLAB的BPSK调制解调仿真(仿真图超多，结果超清晰)

基于MATLAB的BPSK调制解调仿真(仿真图超多，结果超清晰)

基于MATLAB的BPSK调制解调仿真(包含中间各个环节的时域波形、功率谱、频谱图、抽样后的星座图和眼图、理论与仿真的误码率曲线) 目录 前言 一、BPSK基本原理 二、BPSK调制解调过程 三、仿真结果 1、码元信噪比eb/n0-10dB时 1、双极性不归零基带信号 2、成型滤波(根升余弦…
阅读更多...
uni-app应用设置 可以根据手机屏幕旋转进行 (横/竖) 屏切换

uni-app应用设置 可以根据手机屏幕旋转进行 (横/竖) 屏切换

首先 我们打开项目的 pages.json 在左侧导航栏中找到 源码视图 然后找到 app-plus 配置 在下面加上 "orientation": [//竖屏正方向"portrait-primary",//竖屏反方向"portrait-secondary",//横屏正方向"landscape-primary",//横屏反方…
阅读更多...
Other -- ChatGPT 原理

Other -- ChatGPT 原理

本文为个人理解&#xff0c;帮助小白&#xff08;本人就是&#xff09;了解正在创建新时代的 AI 产品&#xff0c;如文中理解有误欢迎留言。 [参考链接--](https://baijiahao.baidu.com/s?id1765556782543603120&wfrspider&forpc) 1. 了解一些基本概念 大语言模型&a…
阅读更多...
安卓MediaRecorder(2)录制源码分析

安卓MediaRecorder(2)录制源码分析

文章目录 前言JAVA new MediaRecorder() 源码分析android_media_MediaRecorder.cpp native_init()MediaRecorder.java postEventFromNativeandroid_media_MediaRecorder.cpp native_setup() MediaRecorder 参数设置MediaRecorder.prepare 分析MediaRecorder.start 分析MediaRec…
阅读更多...
[面试题～Docker] 云原生必问基础篇

[面试题～Docker] 云原生必问基础篇

文章目录 基础相关1. Docker 是什么&#xff1f;2. 镜像是什么3. 容器是什么4. 数据卷是什么5. Docker 和虚拟机的区别&#xff1f;6. Docker 常用命令有哪些&#xff1f; 原理相关1. docker 有几种网络模式host 模式container模式none模式bridge模式 2. docker 网络实现在Linu…
阅读更多...
AGILE-SCRUM

AGILE-SCRUM

一个复杂的汽车ECU开发。当时开发队伍遍布全球7个国家&#xff0c;10多个地区&#xff0c;需要同时为多款车型定制不同的软件&#xff0c;头疼的地方是&#xff1a; 涉及到多方人员协调&#xff0c;多模块集成和管理不同软件团队使用的设计工具、验证工具&#xff0c;数据、工…
阅读更多...
C语言数据结构-基于单链表实现通讯录

C语言数据结构-基于单链表实现通讯录

文章目录 1 基础要求2 通讯录功能2.1 引入单链表的文件2.2 定义联系人数据结构2.3 打开通讯录2.4 保存数据后销毁通讯录2.5 添加联系人2.6 删除联系人2.7 修改联系人2.8 查找联系人2.9 查看通讯录 3 通讯录代码展示3.1 SeqList_copy.h3.2 SeqList_copy.c3.3 Contact.h3.4 Conta…
阅读更多...
【论文阅读】Reachability and distance queries via 2-hop labels

【论文阅读】Reachability and distance queries via 2-hop labels

Cohen E, Halperin E, Kaplan H, et al. Reachability and distance queries via 2-hop labels[J]. SIAM Journal on Computing, 2003, 32(5): 1338-1355. Abstract 图中的可达性和距离查询是许多应用的基础&#xff0c;从地理导航系统到互联网路由。其中一些应用程序涉及到巨…
阅读更多...
免费开源-数字孪生城市污水处理平台

免费开源-数字孪生城市污水处理平台

智慧城市污水处理平台&#xff0c;基于污水厂三维模型可视化场景&#xff0c;结合物联网IOT、视频监控以及综合运营数据&#xff0c;增加污水处理厂的掌控力度。飞渡科技利用数字孪生技术结合物联网IOT技术&#xff0c;直观展现各污水处理站点的整体建设规模&#xff0c;以及污…
阅读更多...
pytorch：YOLOV1的pytorch实现

pytorch：YOLOV1的pytorch实现

pytorch&#xff1a;YOLOV1的pytorch实现 注&#xff1a;本篇仅为学习记录、学习笔记&#xff0c;请谨慎参考&#xff0c;如果错误请评论指出。 参考&#xff1a; 动手学习深度学习pytorch版——从零开始实现YOLOv1 目标检测模型YOLO-V1损失函数详解 3.1 YOLO系列理论合集(YOL…
阅读更多...
Windows Service Name重复问题

Windows Service Name重复问题

Windows Service Name重复问题 1&#xff0c;问题 2&#xff0c;打开命令提示符&#xff0c;管理员身份运行 3&#xff0c;输入命令&#xff1a;sc delete MYSQL57 4&#xff0c;验证一下&#xff0c;可以看见已经没有感叹号啦 &#xff0c;可以看见已经没有感叹号啦
阅读更多...
基于Qt的Live2D模型显示以及控制

基于Qt的Live2D模型显示以及控制

基于Qt的Live2D模型显示以及控制 基本说明 Live2D官方提供有控制Live2D模型的SDK,而且还提供了一个基于OpenGL的C项目Example,我们可以基于该项目改成Qt的项目&#xff0c;做一个桌面端的Live2D桌宠程序。 官方例子 经过改造效果如下图所示。 官方项目配置 下载官方提供的SD…
阅读更多...
视觉检测系统在半导体行业的应用

视觉检测系统在半导体行业的应用

一、半导体产业链概述 半导体产业链是现代电子工业的核心组成部分&#xff0c;涵盖了从原材料到最终产品的整个生产过程。这个产业链主要分为以下几个环节&#xff1a; 1.原材料供应&#xff1a;半导体行业的基石是半导体材料&#xff0c;如硅片、化合物半导体等。这些材料需要…
阅读更多...
CentOS7安装Docker，DockerCompose

CentOS7安装Docker，DockerCompose

安装docker 1、卸载docker 查看是否有旧版本docker docker info首先检测我们虚拟机是否已经安装过Docker&#xff0c;如果安装则需卸载。代码中“\”符号为换行符&#xff0c;相当于一行内容分为多行&#xff0c;这是检测docker的各种组件 yum remove docker \docker-clien…
阅读更多...
高项备考葵花宝典-项目进度管理输入、输出、工具和技术(上，很详细考试必过)

高项备考葵花宝典-项目进度管理输入、输出、工具和技术(上，很详细考试必过)

项目进度管理的目标是使项目按时完成。有效的进度管理是项目管理成功的关键之一&#xff0c;进度问题在项目生命周期内引起的冲突最多。 小型项目中&#xff0c;定义活动、排列活动顺序、估算活动持续时间及制定进度模型形成进度计划等过程的联系非常密切&#xff0c;可以视为一…
阅读更多...
高项备考葵花宝典-项目进度管理输入、输出、工具和技术(中，很详细考试必过)

高项备考葵花宝典-项目进度管理输入、输出、工具和技术(中，很详细考试必过)

项目进度管理的目标是使项目按时完成。有效的进度管理是项目管理成功的关键之一&#xff0c;进度问题在项目生命周期内引起的冲突最多。 小型项目中&#xff0c;定义活动、排列活动顺序、估算活动持续时间及制定进度模型形成进度计划等过程的联系非常密切&#xff0c;可以视为一…
阅读更多...
LeetCode算法题解（单调栈）|LeetCode84. 柱状图中最大的矩形

LeetCode算法题解（单调栈）|LeetCode84. 柱状图中最大的矩形

一、LeetCode84. 柱状图中最大的矩形 题目链接&#xff1a;84. 柱状图中最大的矩形 题目描述&#xff1a; 给定 n 个非负整数&#xff0c;用来表示柱状图中各个柱子的高度。每个柱子彼此相邻&#xff0c;且宽度为 1 。 求在该柱状图中&#xff0c;能够勾勒出来的矩形的最大…
阅读更多...
更改Android Studio的.android和.gradle文件夹默认位置

更改Android Studio的.android和.gradle文件夹默认位置

一、首先关闭Android Studio&#xff0c; 二、目标位置新建文件夹 这一步&#xff0c;为了省去麻烦&#xff0c;我并没有直接在我的目标位置新建文件夹&#xff0c;而是把C盘下的.android和.gradle文件夹整个复制过来&#xff0c;和SDK都在同一目录下&#xff0c;感觉这样可以…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023