原文地址
源代码

Abstract

我们提出了一个简单的、高度模块化的图像分类网络体系结构。我们的网络是通过重复构建块来构建的，该构建块聚合了具有相同拓扑结构的一组变换。我们的简单设计产生了一个同质的、多分支的体系结构，只有几个超参数需要设置。这个策略暴露了一个新的维度，我们称之为“基数”(转换集合的大小)，作为深度和宽度维度之外的一个重要因素。在ImageNet-1K数据集上，我们的经验表明，即使在维持复杂性的限制条件下，增加基数也能够提高分类精度。此外**，当我们增加容量时，增加基数比加深或扩大宽度更有效**。我们的模型ResNeXt是我们进入ILSVRC 2016分类任务的基础，我们在该任务中获得了第二名。我们在ImageNet-5K集和COCO检测集上进一步研究了ResNeXt，也显示出比ResNet更好的结果

1. Introduction

视觉识别研究正经历着从“特征工程”到“网络工程”的过渡[25,24,44,34,36,38,14]。与传统的手工设计特征(例如SIFT[29]和HOG[5])相比，神经网络从大规模数据中学习的特征[33]在训练过程中需要最少的人工参与，并且可以转移到各种识别任务中[7,10,28]。然而，人类的努力已经转移到设计更好的网络架构来学习表征
简要介绍了下以前的backbone，并diss了下他们的不足

former work

VGG-nets展示了一种简单而有效的构建深度网络的策略：把相同形状的块堆叠起来
该策略被ResNets[14]继承，ResNets堆叠相同拓扑的模块。这个简单的规则减少了超参数的自由选择，并且深度暴露为神经网络的一个基本维度。此外，我们认为该规则的简单性可以降低对特定数据集过度适应超参数的风险。VGG-nets和ResNets的鲁棒性已被各种视觉识别任务[7,10,9,28,31,14]以及涉及语音[42,30]和语言[4,41,20]的非视觉任务证明
与VGG-nets不同，Inception模型家族[38,17,39,37]已经证明，精心设计的拓扑结构能够以较低的理论复杂性实现令人信服的准确性
Inception模型随着时间的推移而发展[38,39]，但是一个重要的共同属性是分裂-转换-合并策略。在Inception模块中，输入被分成几个低维嵌入(通过1×1卷积)，由一组专门的过滤器(3×3, 5×5等)进行转换，并通过连接进行合并。可以证明，该体系结构的解空间是运行在高维嵌入上的单个大层(例如5×5)的解空间的严格子空间。Inception模块的拆分-转换-合并行为被期望接近大型和密集层的表示能力，但是在相当低的计算复杂性下

our work

在本文中，我们提出了一个简单的架构，它采用了VGG/ResNets的重复层策略，同时以一种简单、可扩展的方式利用了分裂-转换-合并策略。我们的网络中的一个模块执行一组转换，每个转换都在一个低维嵌入上，其输出通过求和来聚合。我们追求这个想法的一个简单实现——要聚合的转换都是相同的拓扑(例如，图1(右))。这种设计允许我们扩展到任何大量的转换，而无需专门的设计
有趣的是，在这种简化的情况下，我们发现我们的模型还有另外两种等效形式(图3)。图3(b)中的重新表述看起来类似于Inception- ResNet模块[37]，因为它连接了多条路径;但是我们的模块与所有现有的Inception模块的不同之处在于，我们所有的路径都共享相同的拓扑结构，因此路径的数量可以很容易地作为一个要研究的因素被隔离出来。在更简洁的重新表述中，我们的模块可以通过Krizhevsky等人的分组卷积(groups convolutions)24进行重塑，然而，这已经被开发为一种工程折衷方案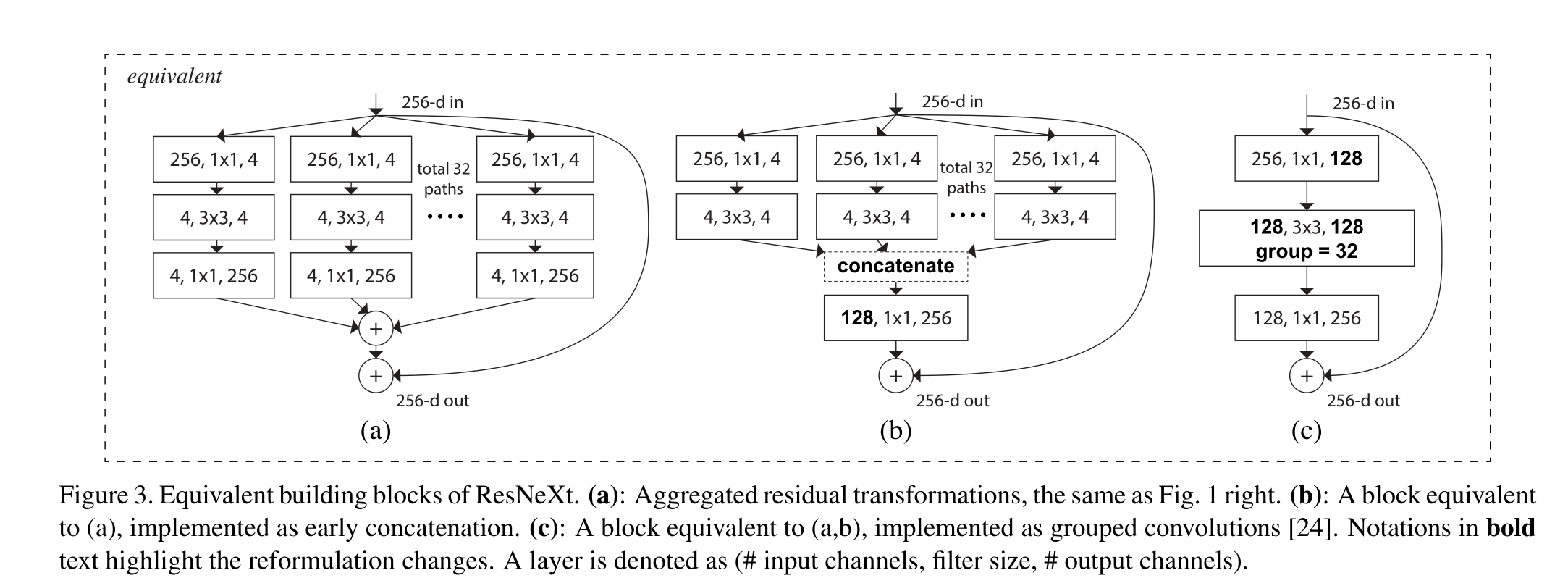

(a):聚合残差变换，与图1右图相同。(b):相当于(A)的块，作为早期连接实现。©:相当于(A,b)的块，实现为分组卷积[24]。加粗文字的注释突出了重新表述的变化。层表示为(#输入通道，过滤器大小，#输出通道)

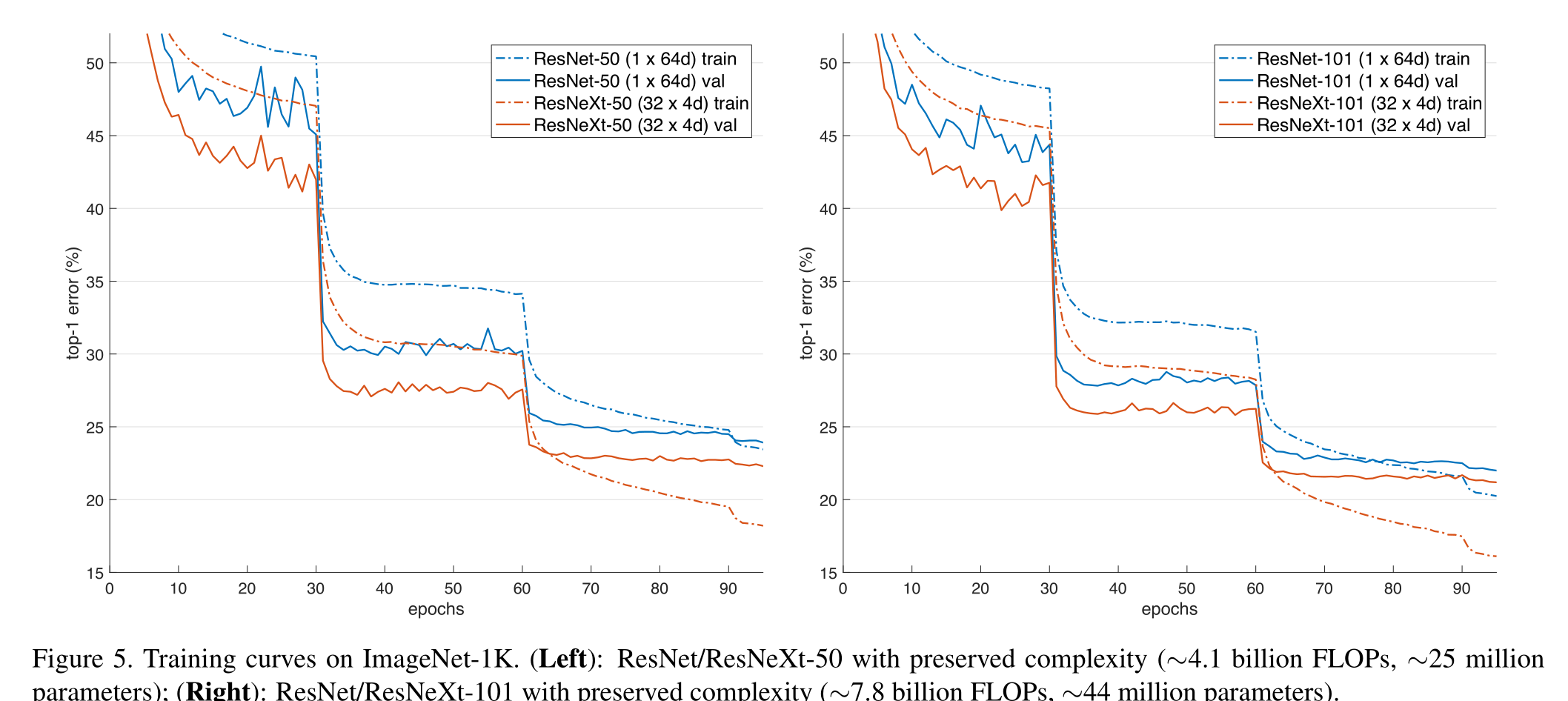
我们通过经验证明，即使在保持计算复杂性和模型大小的限制条件下，我们的聚合变换也优于原始ResNet模块——例如，图1(右)的设计是为了保持图1(左)的FLOPs复杂性和参数数量。我们强调，虽然通过增加容量(更深入或更广泛)来提高准确性相对容易，但在保持(或降低)复杂性的同时提高准确性的方法在文献中很少

我们的方法表明，除了宽度和深度的维度外，基数(变换集的大小)是一个具体的、可测量的维度，这是至关重要的。实验表明，增加基数是一种比深度或宽度更有效的获得精度的方法，特别是当深度和宽度开始使现有模型的收益递减时

我们的神经网络，命名为ResNeXt(建议下一个维度)，在ImageNet分类数据集上优于ResNet-101/152 [14]， ResNet- 200 [15]， Inception-v3[39]和Inception-ResNet-v2[37]。特别是，101层的ResNeXt能够达到比ResNet-200更好的精度[15]，但只有50%的复杂性。此外，ResNeXt展示了比所有Inception模型更简单的设计。ResNeXt是我们参加ILSVRC 2016分类任务的基础，我们获得了第二名。本文在更大的ImageNet-5K集和COCO对象检测数据集上进一步评估了ResNeXt[27]，显示出比ResNet同类产品更好的准确性。我们希望ResNeXt也能很好地推广到其他视觉(和非视觉)识别任务

2. Related Work

多分支卷积网络

Inception模型[38,17,39,37]是成功的多分支架构，其中每个分支都是精心定制的。ResNets[14]可以被认为是一个双分支网络，其中一个分支是身份映射。深度神经决策森林[22]是具有学习分裂函数的树形多分支网络

分组卷积

分组卷积的使用可以追溯到AlexNet论文[24]，如果不是更早的话。Krizhevsky等人[24]给出的动机是将模型分布在两个gpu上。分组卷积由Caffe [19]， Torch[3]等库支持，主要是为了AlexNet的兼容性。据我们所知，很少有证据表明利用分组卷积来提高准确率。**分组卷积的一种特殊情况是通道型卷积，其中组的数量等于通道的数量。**通道型卷积是[35]中可分离卷积的一部分

压缩卷积网络

分解(在空间[6,18]和/或通道[6,21,16]级别)是一种广泛采用的技术，用于减少深度卷积网络的冗余并加速/压缩它们。Ioannou等人[16]提出了一种“根”模式的网络进行约简计算，根中的分支通过分组卷积实现。这些方法[6,18,21,16]在较低的复杂性和较小的模型尺寸下显示了精度的优雅妥协。而不是压缩，我们的方法是一个架构，经验显示出更强的表征能力

Ensembling

对一组独立训练的网络进行平均是提高准确率的有效解决方案[24]，在识别竞赛中被广泛采用[33]。Veit等人[40]将单个ResNet解释为较浅网络的集合，这是由ResNet的加性行为造成的[15]。我们的方法利用加法来聚合一组转换。但我们认为，将我们的方法视为集成是不精确的，因为要聚合的成员是联合训练的，而不是独立训练的。

3. Method

3.1. Template

我们采用高度模块化的VGG/ResNets设计，我们的网络由一堆残差块组成
这些块具有相同的拓扑结构，并且受VGG/ResNets Inception的两个简单规则的约束:(i)如果产生相同大小的空间映射，则块共享相同的超参数(宽度和过滤器大小)，并且(ii)每次当空间映射被下采样2倍时，块的宽度（通道数）乘以2倍。第二条规则确保所有块的计算复杂度(以flop(浮点运算，以乘法加的次数计算)为单位)大致相同
有了这两条规则，我们只需要设计一个模板模块，一个网络中的所有模块都可以据此确定。所以这两条规则大大缩小了设计空间，使我们能够专注于几个关键因素。这些规则构建的网络如表1所示，C指的是基数 。4d指的是通道数为4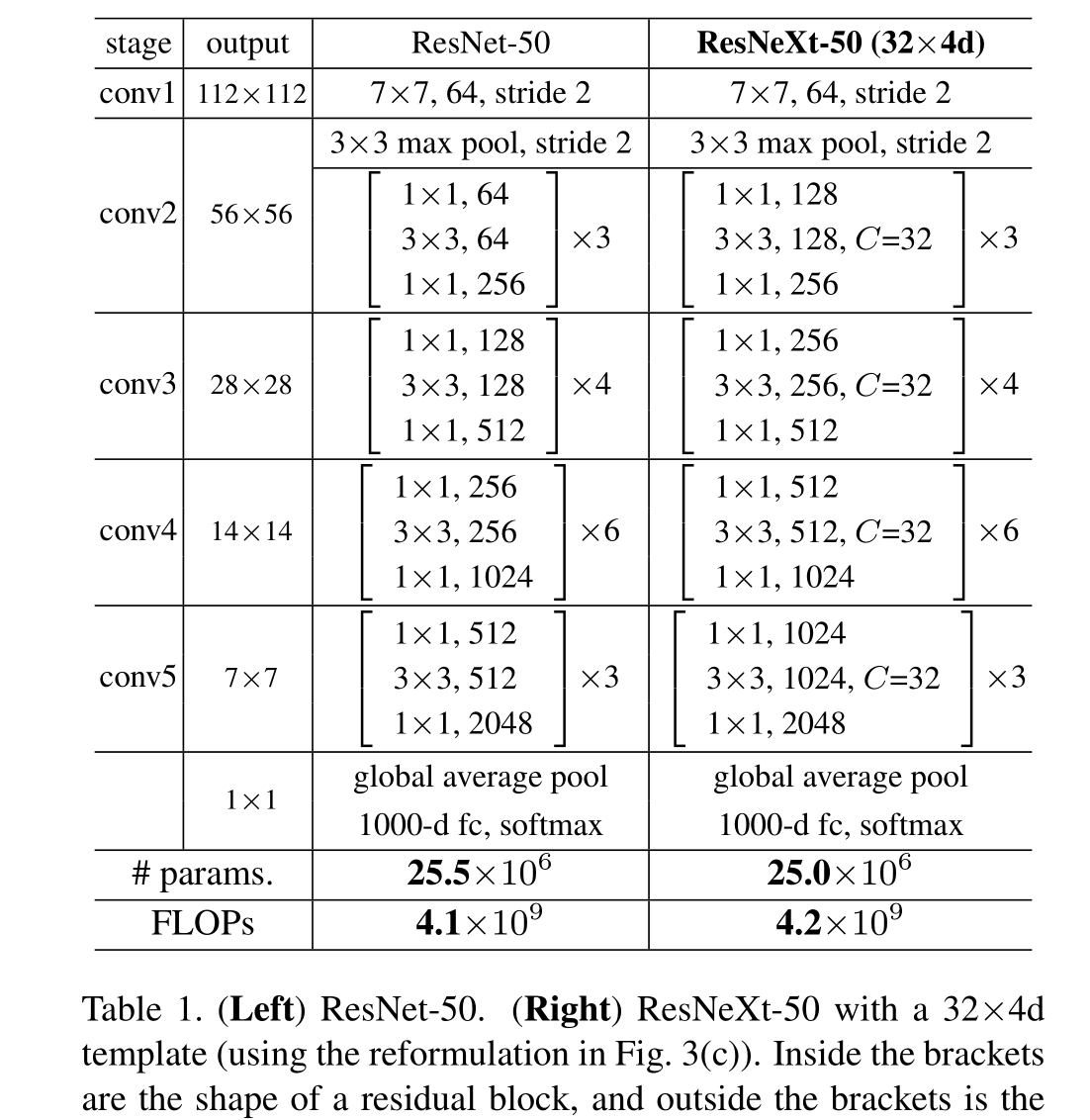

3.2. Revisiting Simple Neurons

人工神经网络中最简单的神经元执行内积(加权和)，这是由全连接层和卷积层完成的初等变换。内积可以看作是集合变换的一种形式:

式中x = [x 1,x 2，…]，x D是神经元的D通道输入向量，w i是第i个通道的滤波器权值。这种操作(通常包括一些非线性输出)被称为“神经元”。见图2

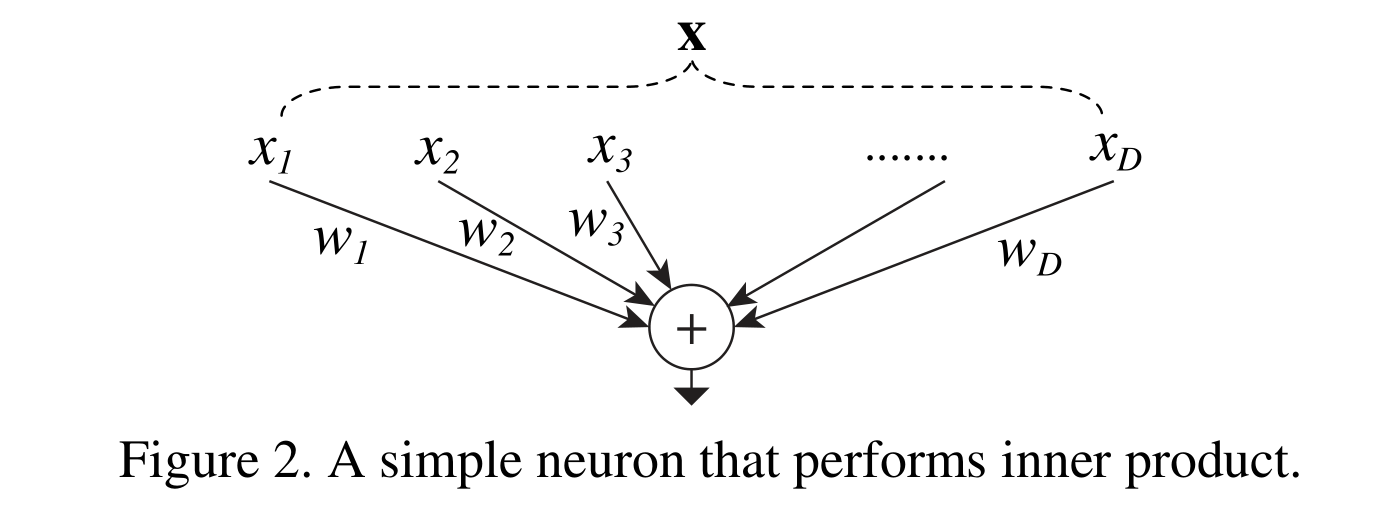
上述操作可以重新转换为拆分、转换和聚合的组合。
(i)分割:将向量x分割为一个低维嵌入，在上面，它是一个一维子空间xi
(ii)变换:对低维表示进行变换，在上面，它被简单地缩放为:wi x i
(iii)聚合:所有嵌入中的转换通过ΣD i=1

3.3. Aggregated Transformations

给定上述对一个简单神经元的分析，我们考虑用一个更一般的函数代替初等变换(wi x i)，它本身也可以是一个网络。与“Network-in-Network”[26]相反，我们表明我们的“Network-in-Neuron”沿着一个新的维度扩展。
形式上，我们将聚合转换表示为:

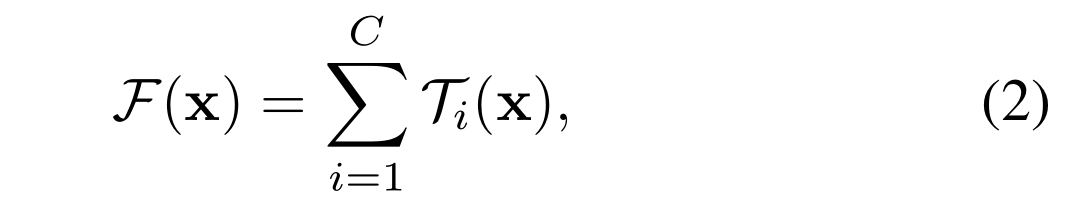
其中Ti (x)可以是任意函数。类似于一个简单的神经元，T i应该将x投射到一个(可选的低维)嵌入中，然后对其进行变换
在公式(2)中，C是要聚合的转换集合的大小。我们将C称为基数[2]。在Eqn.(2)中，C的位置与Eqn.(1)中D的位置相似，但C不必等于D，可以是任意数。虽然宽度的维度与简单变换(内积)的数量有关，但我们认为基数的维度控制着更复杂变换的数量。我们通过实验证明，基数是一个重要的维度，可以比宽度和深度的维度更有效

在本文中，我们考虑了一种设计变换函数的简单方法:所有的T具有相同的拓扑。这扩展了vgg风格的重复相同形状的层的策略，这有助于隔离一些因素并扩展到任何大量的转换。我们将单个转换t1设置为瓶颈形架构[14]，如图1(右)所示。在这种情况下，每个t1中的第一个1×1层产生低维嵌入。

Eqn.(2)中的聚合变换作为残差函数14: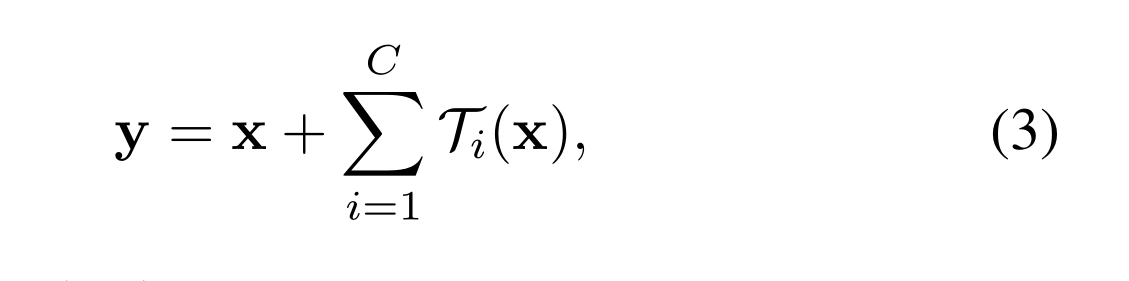
与Inception-ResNet的关系：一些张量操作表明，图1(右)中的模块(也显示在图3(a)中)等价于图3(b)。图3(b)与Inception-ResNet[37]块相似，在残差函数中涉及分支和连接。但与所有Inception或Inception- resnet模块不同，我们在多个路径中共享相同的拓扑结构。我们的模块只需要最少的额外工作来设计每条路径
与分组卷积的关系：使用分组卷积的表示法，上述模块变得更加简洁[24]。图3©说明了这种重新配方。所有的低维嵌入(第一个1×1层)都可以被单个更宽的层(例如，图3©中的1×1, 128-d)所取代。分裂本质上是由分组卷积层在将其输入通道分成组时完成的。图3©中的分组卷积层每形成32组卷积，其输入输出通道为4维。分组卷积层将它们连接起来作为层的输出。图3©中的块看起来与图1(左)中的原始瓶颈剩余块相似，只是图3©是一个更宽但稀疏连接的模块

我们注意到，只有当块的深度≥3时，重新表述才会产生非平凡拓扑。如果该块的深度为2(例如，[14]中的基本块)，则重新表述通常会导致一个宽而密集的模块。如图4所示
讨论：我们注意到，尽管我们提出了显示串联(图3(b))或分组卷积(图3©)的重新表述，但这种重新表述并不总是适用于Eqn(3)的一般形式，例如，如果变换ti采用任意形式并且是异质的。我们在本文中选择使用同质表单，因为它们更简单和可扩展。在这种简化情况下，图3©形式的分组卷积有助于简化实现

3.4. Model Capacity

我们的模型在保持模型复杂性和参数数量的情况下提高了准确性。这不仅在实践中很有趣，更重要的是，参数的复杂性和数量代表了模型的固有能力，因此经常作为深度网络的基本属性进行研究[8]

瓶颈宽度通常指的是ResNeXt中的瓶颈结构中最中间那一层的通道数或特征图的维度。ResNeXt的基本结构由一系列的瓶颈块组成，其中的瓶颈块包含了三个卷积层，中间那一层通常是瓶颈宽度所指的地方。这个瓶颈宽度的选择可以影响模型的复杂度和性能

当我们评估不同的基数C时，同时保持复杂性，我们希望最小化对其他超参数的修改。我们选择调整瓶颈的宽度(例如图1(右)中的4-d)，因为它可以与块的输入和输出隔离。这种策略不会改变其他超参数(深度或块的输入/输出宽度)，因此有助于我们关注基数的影响
在图1(左)中，原始ResNet瓶颈块[14]具有256·64+3·3·64·64+64·256≈70k参数和比例FLOPs(在相同的特征图大小下)。当瓶颈宽度为d时，我们在图1(右)中的模板具有: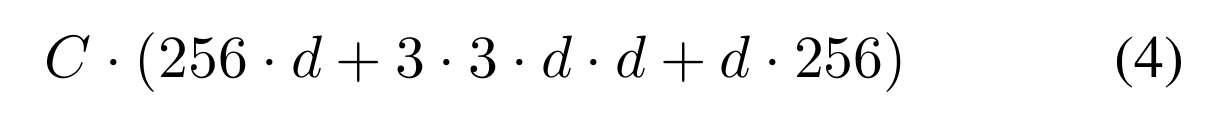
参数和比例FLOPs。当C = 32, d = 4时，Eqn.(4)≈70k。表2显示了基数C和瓶颈宽度d之间的关系

基数和宽度之间的关系(对于conv2的模板)，在残差块上大致保留复杂度。对于conv2的模板，参数的数量为~ 70k。FLOPs的数量为~ 2.2亿(conv2的# params×56×56)

因为我们在3.1节中采用了这两个规则，所以上面的近似相等在ResNet瓶颈块和ResNeXt之间的所有阶段都是有效的(除了特征映射大小变化的子采样层)。表1比较了原始的ResNet-50和具有类似容量的ResNeXt-50。我们注意到，复杂性只能近似地保留，但复杂性的差异很小，不会影响我们的结果

4. Experiment