K-means算法通俗原理及Python与R语言的分别实现

news2025/1/17 14:08:42

K均值聚类方法是一种划分聚类方法，它是将数据分成互不相交的K类。K均值法先指定聚类数，目标是使每个数据到数据点所属聚类中心的总距离变异平方和最小，规定聚类中心时则是以该类数据点的平均值作为聚类中心。

01K均值法原理与步骤

对于有N个数据的数据集，我们想把它们聚成K类，开始需要指定K个聚类中心，假设第i类有ni个样本数据，计算每个数据点分别到聚类中心的距离平方和，距离这里直接用的欧式距离，还有什么海明距离、街道距离、余弦相似度什么的其实都可以，这里聚类的话，欧式距离就好。

（1）、所有类别样本数等于总样本数，即每个类类是互不相同的

K-means算法通俗原理及Python与R语言的分别实现-图片1

（2）、每一类(假设是第i类)中数据点到聚类中心距离平方总和di为：

xi表示第i类各点平均值（聚类中心）

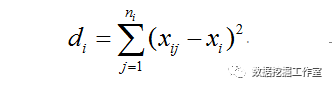
K-means算法通俗原理及Python与R语言的分别实现-图片2

（3）、K类数据点距离之和为：

K-means算法通俗原理及Python与R语言的分别实现-图片3

这样就会有一个KN的距离平方和矩阵，每一列（比如第j列）的最小值对应的行数（比如第i行）就表明：第j个数据样本属于第i类别。这样，每个数据就会分别属于不同的类别了。

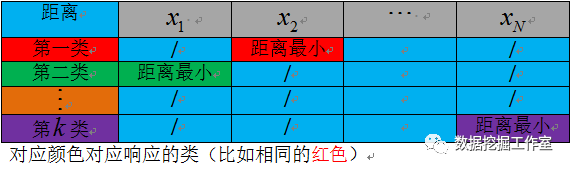
K-means算法通俗原理及Python与R语言的分别实现-图片4

比如，表格中红色部分数据点x2到第一类的聚类中心距离最小，则x2就属于第一类。

K均值步骤：

随机选取K个数据点作为（起始）聚类中心；
按照距离最近原则分配数据点到对应类；
计算每类的数据点平均值（新的聚类中心）；
计算数据点到聚类中心总距离；
如果与上一次相比总距离下降，聚类中心替换；
直到总距离不再下降或者达到指定计算次数。

其实，这个过程相对比较简单，给我一组聚类中心，总能根据到聚类中心距离最小原则生成一组聚类方案，然后计算各个类别到聚类中心距离总和是否下降，如果距离总和下降，就继续计算每类数据点平均值（新的聚类中心），对应的聚类方案要好（还是那句话：给我一组聚类中心，总能根据到聚类中心距离最小原则生成一组聚类方案），然后不断计算，直到距离总和下降幅度很小（几乎收敛），或者达到指定计算次数。

K-means算法缺点主要是：

对异常值敏感；
需要提前确定k值；
结果不稳定；

02 K均值算法Python的实现

思路：

首先用random模块产生随机聚类中心；
用numpy包简化运算；
写了一个函数实现一个中心对应一种聚类方案；
不断迭代；
matplotlib包结果可视化。

代码如下：


   
   import numpy as np
import random as rd
import matplotlib.pyplot as plt
import math
#数据
dat = np.array([[14,22,15,20,30,18,32,13,23,20,21,22,23,24,35,18],
                [15,28,18,30,35,20,30,15,25,23,24,25,26,27,30,16]])
print(dat)
#聚类中心#
n = len(dat[0])
N = len(dat)n
k = 3
#-------随机产生-----#
center = rd.sample(range(n),k)
center = np.array([dat.T[i] for i in center])
print(‘初始聚类中心为：’)
print(center)
print(‘-----------------------’)
 
#计算聚类中心
def cent(x):
   return(sum(x)/len(x))
 
#计算各点到聚类中心的距离之和
def dist(x):
   #聚类中心
   m0 = cent(x)
   dis = sum(sum((x-m0)2))
   return(dis)
 
#距离
def f(center):
   c0 = []
   c1 = []
   c2 = []
   D = np.arange(k*n).reshape(k,n)
   d0 = center[0]-dat.T
   d1 = center[1]-dat.T
   d2 = center[2]-dat.T
   d = np.array([d0,d1,d2])
   for i in range(k):
      D[i] = sum((d[i]2).T)
   for i in range(n):
      ind = D.T[i].argmin()
      if(ind  0):
         c0.append(i)#分配类别
      else:
         if(ind  1):
            c1.append(i)
         else:
            c2.append(i)
   C0 = np.array([dat.T[i] for i in c0])
   C1 = np.array([dat.T[i] for i in c1])
   C2 = np.array([dat.T[i] for i in c2])
   C = [C0,C1,C2]
   print([c0,c1,c2])
   s = 0
   for i in C:
      s+=dist(i)
   return(s,C)
 
n_max = 50
#初始距离和
print(‘第1次计算！’)
dd,C = f(center)
print(‘距离和为’+str(dd))
print(‘第2次计算！’)
center = [cent(i) for i in C]
Dd,C = f(center)
print(‘距离和为’+str(Dd))
K = 3
 
while(K<n_max):
   #两次差值很小并且计算了一定次数
   if(math.sqrt(dd-Dd)<1 and K>20):
      break;
   print(‘第’+str(K)+‘次计算！’)
   dd = Dd
   print(‘距离和为’+str(dd))
   #当前聚类中心
   center = [cent(i) for i in C]
   Dd,C = f(center)
   K+=1
 
 
#—聚类结果可视化部分—#
 
j = 0
for i in C:
   if(j  0):
      plt.plot(i.T[0],i.T[1],‘ro’)
   if(j  1):
      plt.plot(i.T[0],i.T[1],‘b+’)
   if(j == 2):
      plt.plot(i.T[0],i.T[1],‘g*’)
   j+=1
 
plt.show()

（1）：聚类成功的例子：

对于不合适的初始随机聚类中心，一般而言不会失败，成功次数较多。

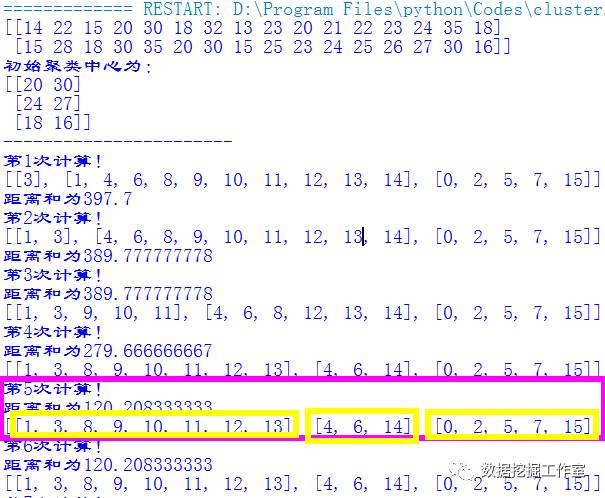
K-means算法通俗原理及Python与R语言的分别实现-图片5

可以看出，其实第五次就收敛了，共分成了三类。它们的标签序号为：

第一类：[1, 3, 8, 9, 10, 11, 12, 13]；

第二类：[4, 6, 14]；

第三类：[0, 2, 5, 7, 15]

聚类图：

K-means算法通俗原理及Python与R语言的分别实现-图片6

聚类结果与实际情况一致

（2）：聚类失败的例子：

有时候可能会失败，运行实验了三次出现了一次败笔，迭代过程如下：

K-means算法通俗原理及Python与R语言的分别实现-图片7

散点图：

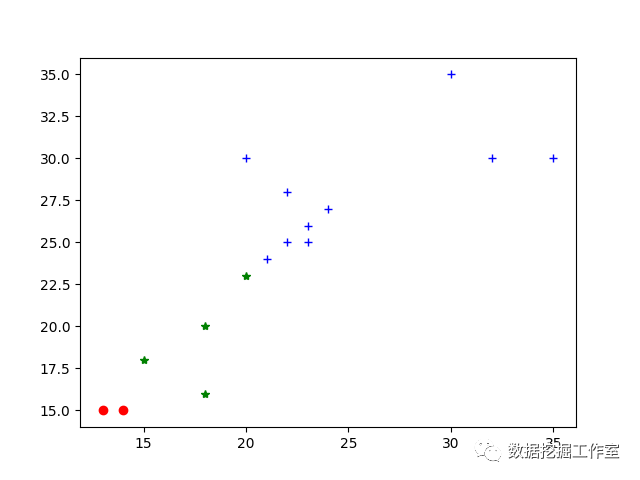
K-means算法通俗原理及Python与R语言的分别实现-图片8

聚类失败图

显然，由于初始点的随机选取不当，导致聚类严重失真！这聚类效果明显就很差，表明随机产生的初始聚类中心应该不合适，最后不管怎么迭代，都不可能生成合适的聚类了，这与k-means算法的原理确实可以解释的。这就是k-means的最显著的缺点！

03K均值算法的R语言实现

用的还是上面程序一样的数据，R语言聚类就很方便，直接调用kmeans(data,聚类数)就能方便完成：

  
  rm(list = ls())
path <- ‘C:\Users\26015\Desktop\clu.txt’
dat <- read.csv(path,header = FALSE)
dat <- t(dat)
kc <- kmeans(dat,3)
summary(kc)
kc

查看聚类结果：

  
  K-means clustering with 3 clusters of sizes 8, 3, 5
 
Cluster means:
      [,1]     [,2]
1 21.87500 26.00000
2 32.33333 31.66667
3 15.60000 16.80000