Problem: 78. 子集
文章目录
- 题目描述
- 思路
- 解题方法
- 复杂度
- Code
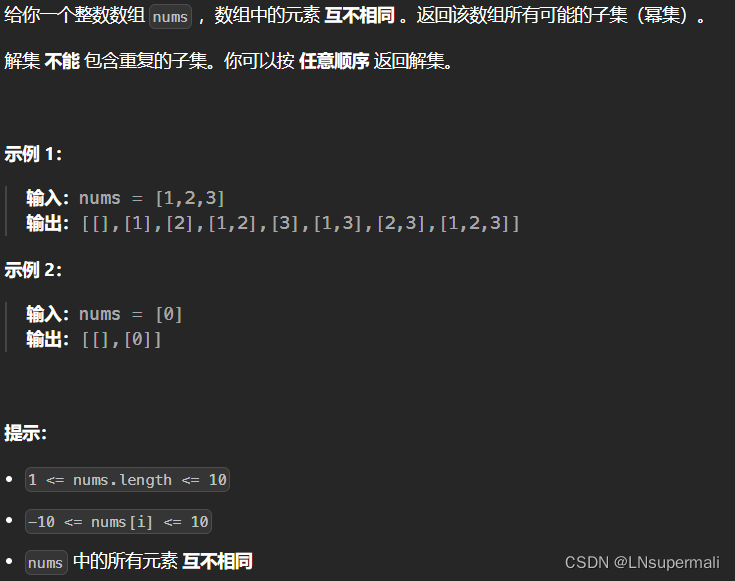
题目描述
思路
我们易知,本题目涉及到对元素的穷举,即我们可以使用回溯来实现。对于本题目我们应该较为注重回溯中的决策阶段:
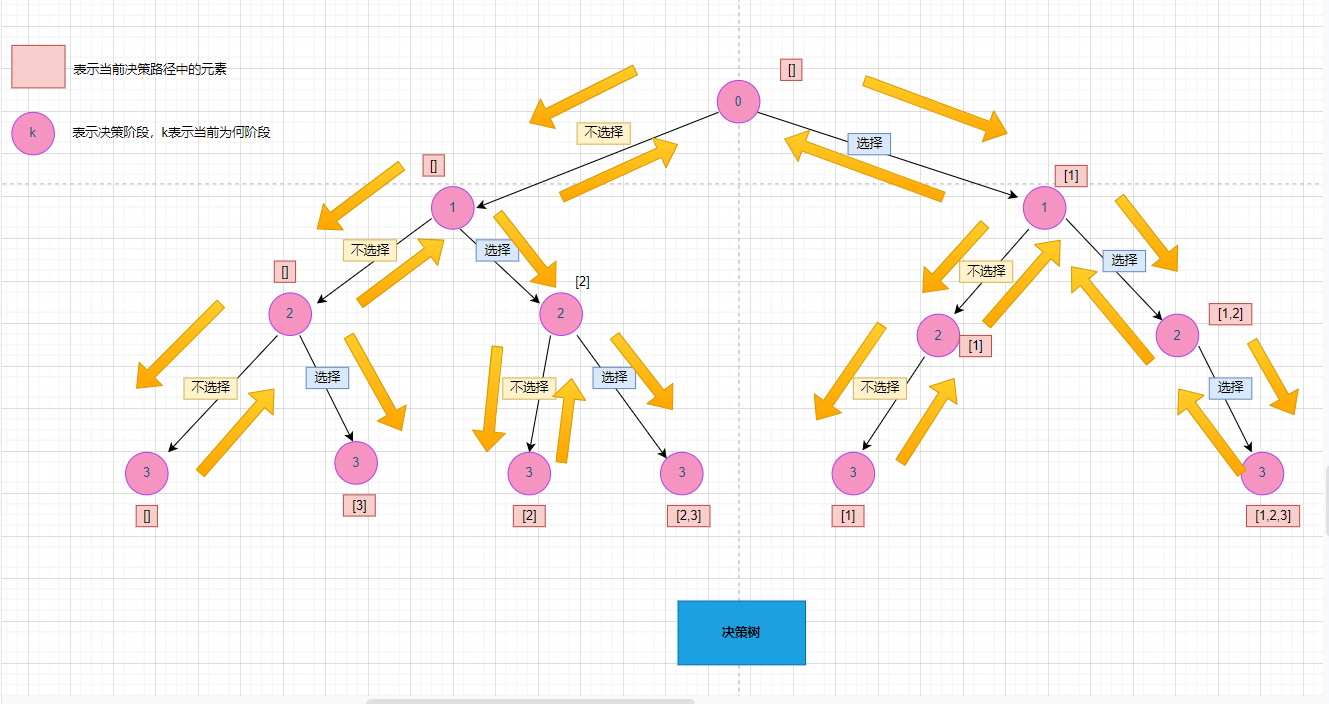
由于涉及到对数组中元素的穷举,即在每一决策阶段,我们涉及到是否选择当前元素(是否将当前决策阶段的元素添加到决策路径中),即我们可以利用递归先将所有的不选择添加到决策路径的元素,递完,再在归的过程中继续递归选择添加到决策路径(描述的可能比较模糊,直接看决策树与代码更便于理解!!!)
解题方法
1.定义成员变量result(二维集合)
2.调用并编写回溯函数(从阶段0开始回溯(实际上只是便于配合数组元素的下标索引为0))
3.回溯函数:3.1当决策阶段(假设为k)等于题目所给的数组nums的长度时,则将当前的决策路径添加到二维结果集result
3.2先递归所有不选择当前决策阶段元素,再在归的过程中先添加当前决策阶段的元素到决策路径,再继续递归选择当前决策阶段元素
3.3在递完选择当前决策阶段元素后需要删除当前决策路径中的最后一个元素
复杂度
时间复杂度:
O ( n × 2 n ) O(n \times 2^n) O(n×2n)
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {
//Two-dimensional result set
private List<List<Integer>> result = new ArrayList<>();
/**
*Return all subsets
* @param nums Universal set
* @return List<List<Integer>>
*/
public List<List<Integer>> subsets(int[] nums) {
backtrack(nums, 0, new ArrayList<Integer>());
return result;
}
/**
* Backtracking function is used to find all subsets
* @param nums Optional combination
* @param k Decision stage
* @param path Decision path
*/
private void backtrack(int[] nums, int k, List<Integer> path) {
if (k == nums.length) {
result.add(new ArrayList<>(path));
return;
}
//Recursion that does not select the current decision stage element
backtrack(nums, k + 1, path);
//Add the current decision stage element to decision stage
path.add(nums[k]);
//Recursion which selects the current decision stage element
backtrack(nums, k + 1, path);
//Remove the last element of current decision path
path.remove(path.size() - 1);
}
}







![[Geek Challenge 2023] klf_2详解](https://img-blog.csdnimg.cn/direct/71bc278765e448579e65bcf487d8200b.png)

