上期我们实现了快速排序的递归实现，但是我们知道如果递归深度太深，栈就会溢出，所以我们本期将为大家讲述快速排序的非递归实现，我们需要用到栈的数据结构，我们知道栈中的数据全是在堆区开辟的空间，堆的空间大小是比栈的大小要大的，这便是我们为什么要采用非递归的方法实现快排的原因。

快速排序非递归实现

        在学习非递归之前，我们先回顾一下，使用递归方法实现排序的方法，我们依旧采用第一种单趟排序的方法。这种方法单趟排序的目的就是最终找一个key，如果是排升序，最终k位置左边的所有元素都比key位置上的元素小，右边的所有元素都比key位置上的元素大。也就意味着，最终找到了一个key位置，这个位置上的元素已经排好了序。

        当我们进行完单趟排序之后，找到了一个key值，因为这个位置的元素已经排好了序，所以我们只需要对这个key位置左边和右边的所有元素进行快速排序即可，这就是我们实现快速排序的递归方法。单趟排序一次只能排好一个元素。

那么如何进行非递归呢?

         非递归的实现其实是在递归的方法上进行改进的，就是将递归中的操作改成用循环来实现。因为单趟排序一次可以排好一个元素，那么n个元素总共就需要n-1次单趟排序，然后我们就可以利用循环来进行所有的单趟排序，每一次单趟排序都会返回一个key，我们要根据key的位置确定下一次单趟排序的元素的下标范围。假如我们现在已经确定了一个key，那么此时我们要么开始对右边进行单趟排序，要么对左边的元素进行单趟排序，但是一旦我们选择了左边，那么就必须将左边的所有元素排好序之后才能去排右边的元素，所以我们如果先排了左边，那么就需要将右边的元素的下标范围存储起来，以便于最后将左边元素排好之后返回来进行右边的排序。怎么样保存，这便就用到了栈的数据结构。如果先对左边的所有元素进行单趟排序，后对右边的所有元素进行单趟排序，根据栈先进后出的性质，那么就得先将右边元素的下标入栈，再将左边的元素的下标入栈。因为当数组中只有一个元素时是没有必要进行单趟排序的，所以要进行单趟排序必须保证数组中至少有两个元素，这就是我们是否继续进行单趟排序的条件。

以上便是非递归的思路，总的来说，有些复杂，大家仔细阅读几遍。

 图示如下： 

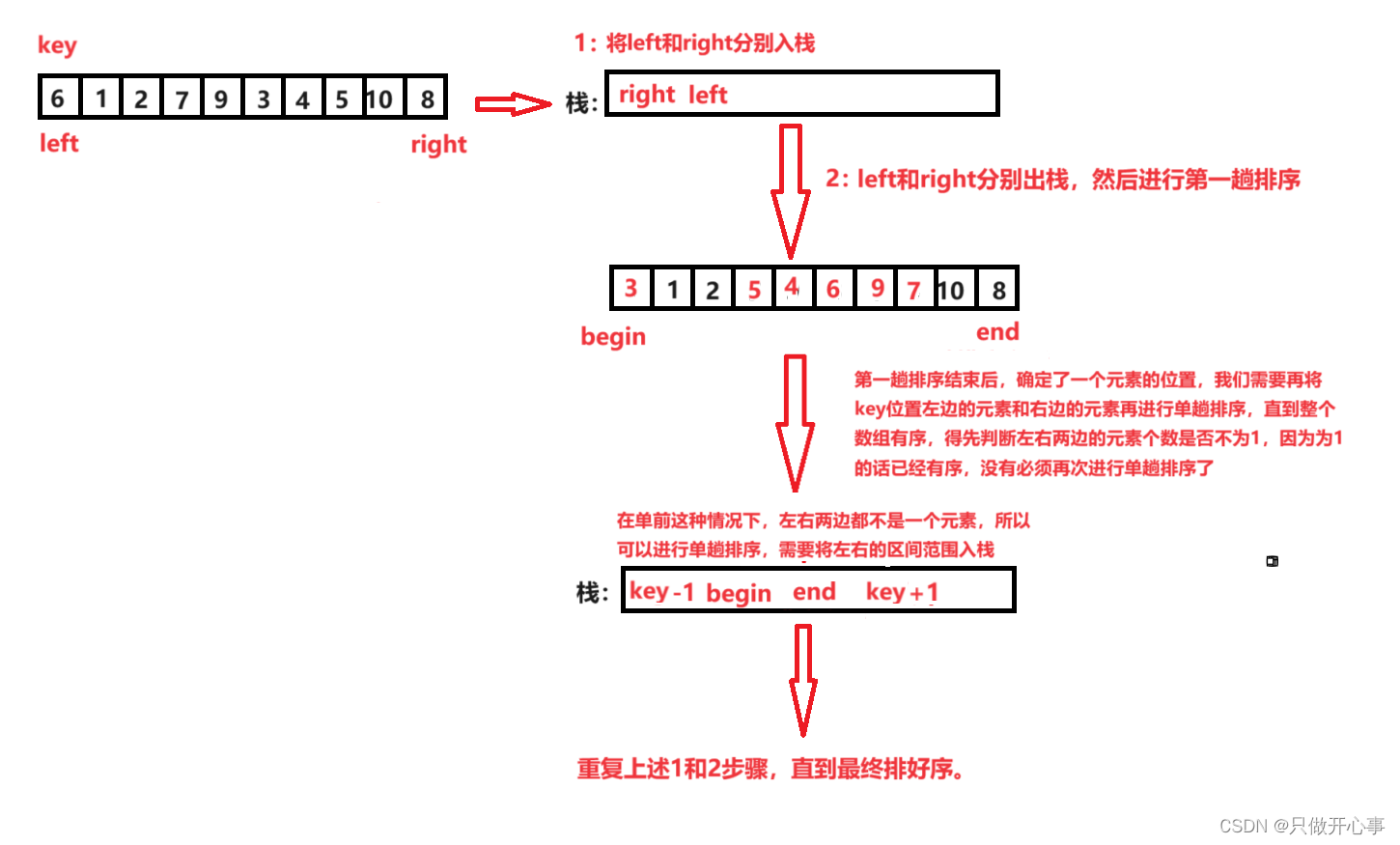
非递归整体代码如下：

void QuickSortNR(int* a, int left, int right)
{
	 ST Stack;
	 StackInit(&Stack);
	 StackPush(&Stack, right);
	 StackPush(&Stack, left);
	 while (!StackEmpty(&Stack))
	 {
		 int begin = StackTop(&Stack);
		 StackPop(&Stack);
		 int end = StackTop(&Stack);
		 StackPop(&Stack);
		 int key = PartSort1(a, begin, end);
		 if (begin < key - 1)
		 {
			 StackPush(&Stack, key - 1);
			 StackPush(&Stack, begin);
		 }
		 if (key + 1 < end)
		 {
			 StackPush(&Stack, end);
			 StackPush(&Stack, key + 1);
		 }
	 }
	 StackDestroy(&Stack);
}

注意：我们使用非递归实现快速排序时，最重要的还是要保证栈中元素的变化，只有当栈中存在元素时我们才进行循环，栈中存放的就是我们每次进行单趟排序的区间。 

到此，快速排序的所有知识点我们已经学习完，总而言之，在我们多次的优化下，快速排序已经是一个非常优秀的排序了。

本期内容到此结束^_^