2023-12-06每日一题

一、题目编号

2646. 最小化旅行的价格总和

二、题目链接

点击跳转到题目位置

三、题目描述

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

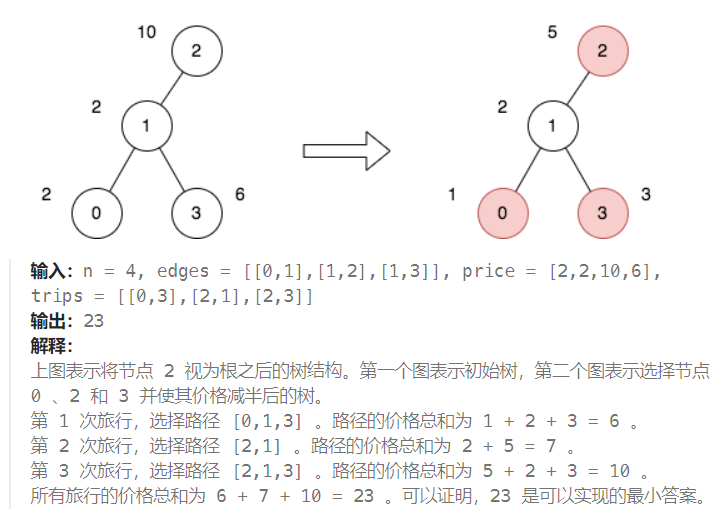
示例 2：

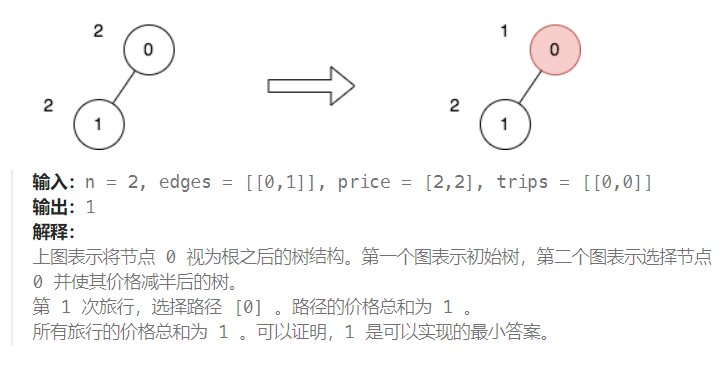
提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= a_i, b_i <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= start_i, end_i <= n - 1

四、解题代码

class Solution {
public:
    int minimumTotalPrice(int n, vector<vector<int>> &edges, vector<int> &price, vector<vector<int>> &trips) {
        vector<vector<int>> next(n);
        for (auto &edge : edges) {
            next[edge[0]].push_back(edge[1]);
            next[edge[1]].push_back(edge[0]);
        }

        vector<int> count(n);
        function<bool(int, int, int)> dfs = [&](int node, int parent, int end) -> bool {
            if (node == end) {
                count[node]++;
                return true;
            }
            for (int child : next[node]) {
                if (child == parent) {
                    continue;
                }
                if (dfs(child, node, end)) {
                    count[node]++;
                    return true;
                }
            }
            return false;
        };
        for (auto &trip: trips) {
            dfs(trip[0], -1, trip[1]);
        }

        function<pair<int, int>(int, int)> dp = [&](int node, int parent) -> pair<int, int> {
            pair<int, int> res = {
                price[node] * count[node], price[node] * count[node] / 2
            };
            for (int child : next[node]) {
                if (child == parent) {
                    continue;
                }
                auto [x, y] = dp(child, node);
                res.first += min(x, y); // node 没有减半，因此可以取子树的两种情况的最小值
                res.second += x; // node 减半，只能取子树没有减半的情况
            }
            return res;
        };
        auto [x, y] = dp(0, -1);
        return min(x, y);
    }
};

五、解题思路

(1) 深度优先搜索+贪心。